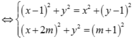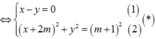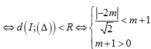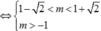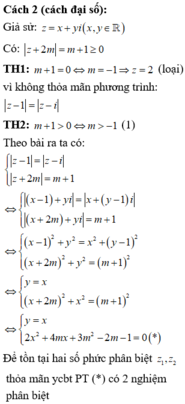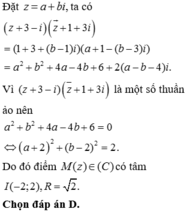Tìm tất cả các tập hợp Z sao cho \([1;2]\subset X\subset\)\([1;2;3;4;5]\)

Những câu hỏi liên quan
Cho các tập hợp A=(-3;4]; B=[-5;1)
a, Tìm các tập hợp A\(\cap\)B; \(A\cup B\) ; A\B; CRA
b, Cho tập C={ x∈Z: x2-6|x|+5=0}; Tìm tất cả tập con của \(B\cap C\)
c, Cho m là số thực âm. Tìm tất cả các giá trị của m để A⊂D với D=(-4; \(1-\dfrac{1}{m}\) )
a: \(A\cap B=\left(-3;1\right)\)
\(A\cup B\)=[-5;4]
A\B=[1;4]
\(C_RA\)=R\A=(-∞;-3]\(\cap\)(4;+∞)
b: C={1;-1;5;-5}
\(B\cap C=\left\{-5;-1\right\}\)
Các tập con là ∅; {-5}; {-1}; {-5;-1}
Đúng 1
Bình luận (0)
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt
z
1
,
z
2
thỏa mãn đồng thời các phương trình
z
-
1
z
-
i
và
z
+
2
m
m...
Đọc tiếp
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn đồng thời các phương trình z - 1 = z - i và z + 2 m = m + 1 . Tổng tất cả các phần tử của S là
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt
z
1
,
z
2
thỏa mãn đồng thời các phương trình
z
-
1
z
-
i
và
z
+
2
m
m...
Đọc tiếp
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn đồng thời các phương trình z - 1 = z - i và z + 2 m = m + 1 . Tổng tất cả các phần tử của S là
A. 1
B. 4
C. 2
D. 3
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt
z
1
,
z
2
thỏa mãn đồng thời các phương trình
z
-
1
z
-
i
và
z
+
2
m...
Đọc tiếp
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn đồng thời các phương trình z - 1 = z - i và z + 2 m = m + 1 . Tổng tất cả các phần tử của S là
A. 1
B. 4
C. 2
D. 3
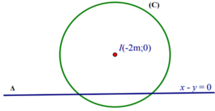
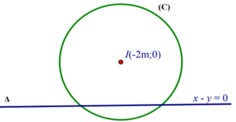
Cách 1 (cách hình học): Gọi M ( x ; y ) x . y ∈ ℝ là điểm biểu diễn của số phức z thỏa mãn yêu cầu bài toán.
Có: z + 2 m = m + 1 ≥ 0
TH1: m + 1 = 0 ⇔ ⇔ m = - 1 ⇒ z = 2 (loại) vì không thỏa mãn phương trình: z - 1 = z - i
TH2: m + 1 > 0 ⇔ m > - 1
Theo bài ra ta có:
z - 1 = z - i z + 2 m = m + 1 ⇔ x - 1 + y i = x + y - 1 i x + 2 m + y i = m + 1 ⇔ x - 1 2 + y 2 = x 2 + y - 1 2 x + 2 m 2 + y 2 = m + 1 2 ⇔ x - y = 0 1 x + 2 m 2 + y 2 = m + 1 2 2 *
Từ (1) suy ra: tập hợp điểm M(x;y) biểu diễn của số phức z là đường thẳng: ( ∆ ) : x - y = 0
Từ (2) suy ra: tập hợp điểm M(x;y) biểu diễn của số phức z là đường tròn
( C ) : T â m I ( - 2 m ; 0 ) b k R = m + 1
Khi đó: M ∈ ∆ ∩ ( C ) ⇒ số giao điểm M chính là số nghiệm của hệ phương trình (*).
Để tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn ycbt ⇔ ( C ) cắt ∆ tại hai điểm phân biệt
⇔ d I , ∆ < R ⇔ - 2 m 2 < m + 1 m + 1 > 0 ⇔ - m + 1 < 2 m < m + 1 m + 1 > 0 ⇔ 1 - 2 < m < 1 + 2 m > - 1
Vì m ∈ ℝ ⇒ m ∈ S 0 ; 1 ; 2 . Vậy tổng các phần tử của S là 0+1+2=3.
Cách 2 (cách đại số):
Giả sử: z = x + y i x ; y ∈ ℝ
Có: z + 2 m = m + 1 ≥ 0
TH1: m + 1 = 0 ⇔ ⇔ m = - 1 ⇒ z = 2 (loại) vì không thỏa mãn phương trình: z - 1 = z - i
TH2: m + 1 > 0 ⇔ m > - 1 (1)
Theo bài ra ta có:
z - 1 = z - i z + 2 m = m + 1 ⇔ x - 1 + y i = x + y - 1 i x + 2 m + y i = m + 1 ⇔ x - 1 2 + y 2 = x 2 + y - 1 2 x + 2 m 2 + y 2 = m + 1 2 ⇔ y = x x + 2 m 2 + x 2 = m + 1 2 ⇔ y = x 2 x 2 + 4 m x + 3 m 2 - 2 m + 1 = 0 *
Để tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn ycbt PT (*) có 2 nghiệm phân biệt
⇔ ∆ ' = 4 m 2 - 2 ( 3 m 2 - 2 m - 1 ) = 2 - m 2 + 2 m + 1 > 0 ⇔ 1 - 2 < m < 1 + 2 ( 2 )
Kết hợp điều kiện (1) và (2), m ∈ ℝ ⇒ m ∈ S = 0 ; 1 ; 2
Vậy tổng các phần tử của S là: 0+1+2=3
Chọn đáp án D.
Đúng 0
Bình luận (0)
Bài 1: tìm tập hợp con của tập hợp Q={1;4;5;7;9}sao cho mỗi tập hợp con đó đều có
Bài 2:Cho tập hợp M={1;2;a}.Viết tất cả tập hợp con của M.
Bài 3:Cho tập hợp N={1;5;6;7;8;10}.Viết tất cả các tập hợp con của N.
Tập hợp tất cả các điểm biểu diễn số phức z sao cho
z
+
3
-
i
z
¯
+
1
+
3
i
là một số thuần ảo là một đường tròn có bán kính bằng A.
2
2
B. ...
Đọc tiếp
Tập hợp tất cả các điểm biểu diễn số phức z sao cho z + 3 - i z ¯ + 1 + 3 i là một số thuần ảo là một đường tròn có bán kính bằng
A. 2 2
B. 14
C. 5
D. 2
Tìm tất cả các tập hợp X sao cho: { 1; 2 } \(\subset X\subset\left\{1;2;3;4;5;6\right\}\)
X = {1; 2}
X = {1; 2; 3}
X = {1; 2; 4}
X = {1; 2; 5}
X = {1; 2; 6}
X = {1; 2; 3; 4}
X = {1; 2; 3; 5}
X = {1; 2; 3; 6}
X = {1; 2; 4; 5}
X = {1; 2; 4; 6}
X = {1; 2; 5; 6}
X = {1; 2; 3; 4; 5}
X = {1; 2; 3; 4; 6}
X = {1; 2; 3; 5; 6}
X = {1; 2; 4; 5; 6}
X = {1; 2; 3; 4; 5; 6}
Đúng 1
Bình luận (0)
X={1;2}
X={1;2;3}
X={1;2;3;4}
X={1;2;3;4;5}
X={1;2;3;4;5;6}
Đúng 0
Bình luận (0)
X có thể là: {1;2;3} hoặc {1;2;4} hoặc {1;2;5} hoặc {1;2;6} hoặc {1;2;3;4} hoặc {1;2;3;5} hoặc {1;2;3;6}; hoặc {1;2;4;5} hoặc {1;2;4;6} hoặc {1;2;5;6} hoặc {1;2;3;4;5} hoặc {1;2;3;4;6} hoặc {1;2;3;5;6}
Đúng 0
Bình luận (0)
Bài 1 Cho tập hợp B={x;y;z}.Hỏi tập hợp B có tất cả bao nhiêu tập hợp con ?
Bài 2 Cho A ={1;2;3}.Tìm tất cả các tập hợp con của tập hợp A
a,Viết các tập hợp con của A có hai phần tử
b,Có bao nhiêu tập hợp con của A có ba phần tử ?
c,Có bao nhiêu tập hợp con của A có bốn phần tử?
d,Tập hợp A có bao nhiêu tập hợp con?
bài 1
6 tập hợp con
bài 2
{1};{2};{3};{1;2};{1;3};{2;3}
a){1;2};{1;3};{2;3}
b)có 0
c)có 0
d)6
Đúng 0
Bình luận (0)
Bài 1 bạn kia trả lời sai nhé. Có 7 tập hợp con. Tập hợp con thứ 7 chính là tập hợp rỗng. Vì tập rỗng là tập hợp con của mọi tập hợp bạn nhé
Đúng 1
Bình luận (0)
Trong các tập hợp sau đây, tập nào là tập rỗng:
a/A={x ∈ Z | |x| < 1}
b/B={x ∈ R | x2 - x + 1= 0}
c/C={x ∈ N | x2 + 7x + 12 = 0}
Cho tập hợp A ={1;2;3}
a/ Viết tất cả các tập hợp con gồm 2 phần tử của tập hợp A
b/ Viết tất cả các tập hợp con của tập hợp A
Tìm tất cả các tập X sao cho{1;3} ⊂ X ⊂{1;2;3;4;5}
Tập hợp C rỗng vì \(x^2+7x+12=0\Leftrightarrow x\in\left\{-3;-4\right\}\notin N\)
\(a,\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\}\\ b,\left\{1\right\};\left\{2\right\};\left\{3\right\};\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\};\left\{1;2;3\right\}\)
\(X=\left\{1;3\right\}\\ X=\left\{1;2;3\right\}\\ X=\left\{1;3;4\right\}\\ X=\left\{1;3;5\right\}\\ X=\left\{1;2;3;4\right\}\\ X=\left\{1;2;3;5\right\}\\ X=\left\{1;3;4;5\right\}\\ X=\left\{1;2;3;4;5\right\}\)
Đúng 1
Bình luận (0)