Cách 1 (cách hình học): Gọi M ( x ; y ) x . y ∈ ℝ là điểm biểu diễn của số phức z thỏa mãn yêu cầu bài toán.
Có: z + 2 m = m + 1 ≥ 0
TH1: m + 1 = 0 ⇔ ⇔ m = - 1 ⇒ z = 2 (loại) vì không thỏa mãn phương trình: z - 1 = z - i
TH2: m + 1 > 0 ⇔ m > - 1
Theo bài ra ta có:
z - 1 = z - i z + 2 m = m + 1 ⇔ x - 1 + y i = x + y - 1 i x + 2 m + y i = m + 1 ⇔ x - 1 2 + y 2 = x 2 + y - 1 2 x + 2 m 2 + y 2 = m + 1 2 ⇔ x - y = 0 1 x + 2 m 2 + y 2 = m + 1 2 2 *
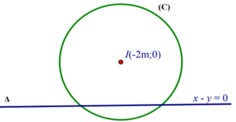
Từ (1) suy ra: tập hợp điểm M(x;y) biểu diễn của số phức z là đường thẳng: ( ∆ ) : x - y = 0
Từ (2) suy ra: tập hợp điểm M(x;y) biểu diễn của số phức z là đường tròn
( C ) : T â m I ( - 2 m ; 0 ) b k R = m + 1
Khi đó: M ∈ ∆ ∩ ( C ) ⇒ số giao điểm M chính là số nghiệm của hệ phương trình (*).
Để tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn ycbt ⇔ ( C ) cắt ∆ tại hai điểm phân biệt
⇔ d I , ∆ < R ⇔ - 2 m 2 < m + 1 m + 1 > 0 ⇔ - m + 1 < 2 m < m + 1 m + 1 > 0 ⇔ 1 - 2 < m < 1 + 2 m > - 1
Vì m ∈ ℝ ⇒ m ∈ S 0 ; 1 ; 2 . Vậy tổng các phần tử của S là 0+1+2=3.
Cách 2 (cách đại số):
Giả sử: z = x + y i x ; y ∈ ℝ
Có: z + 2 m = m + 1 ≥ 0
TH1: m + 1 = 0 ⇔ ⇔ m = - 1 ⇒ z = 2 (loại) vì không thỏa mãn phương trình: z - 1 = z - i
TH2: m + 1 > 0 ⇔ m > - 1 (1)
Theo bài ra ta có:
z - 1 = z - i z + 2 m = m + 1 ⇔ x - 1 + y i = x + y - 1 i x + 2 m + y i = m + 1 ⇔ x - 1 2 + y 2 = x 2 + y - 1 2 x + 2 m 2 + y 2 = m + 1 2 ⇔ y = x x + 2 m 2 + x 2 = m + 1 2 ⇔ y = x 2 x 2 + 4 m x + 3 m 2 - 2 m + 1 = 0 *
Để tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn ycbt PT (*) có 2 nghiệm phân biệt
⇔ ∆ ' = 4 m 2 - 2 ( 3 m 2 - 2 m - 1 ) = 2 - m 2 + 2 m + 1 > 0 ⇔ 1 - 2 < m < 1 + 2 ( 2 )
Kết hợp điều kiện (1) và (2), m ∈ ℝ ⇒ m ∈ S = 0 ; 1 ; 2
Vậy tổng các phần tử của S là: 0+1+2=3
Chọn đáp án D.



