Tìm m để phương trình sau có nghiệm
\(2sin^2x-sinx-m+3=0\)
Bài 1: Tìm m để các phương trình sau có nghiệm
a) \((m+2)sinx+mcosx=2\)
b) \(msinx+(m-1)cosx=2m+1\)
c) \((m+2)sin2x+mcos^2x=m-2+msin^2x\)
Bài 2: Tìm m để các phương trình sau vô nghiệm
a) \((2m-1)sinx+(m-1)cosx=m-3\)
b) \(2sinx+cosx=m(sinx-2cosx+3)\)
1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
1.
c, \(\left(m+2\right)sin2x+mcos^2x=m-2+msin^2x\)
\(\Leftrightarrow\left(m+2\right)sin2x+m\left(cos^2x-sin^2x\right)=m-2\)
\(\Leftrightarrow\left(m+2\right)sin2x+mcos2x=m-2\)
Phương trình vô nghiệm khi:
\(\left(m+2\right)^2+m^2< \left(m-2\right)^2\)
\(\Leftrightarrow m^2+4m+4+m^2< m^2-4m+4\)
\(\Leftrightarrow m^2+8m< 0\)
\(\Leftrightarrow-8\le m\le0\)
cho phương trình \(2cos2x+sin^2xcosx+sinxcos^2x=m\left(sinx+cosx\right)\)tìm m để phương trình có ít nhất 1 nghiệm thuộc đoạn\(\left[0;\dfrac{\Pi}{2}\right]\)
\(\Leftrightarrow2\left(cos^2x-sin^2x\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left(2cosx-2sinx\right)\left(sinx+cosx\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(\text{vô nghiệm trên đoạn xét}\right)\\2cosx-2sinx+sinx.cosx=m\left(1\right)\end{matrix}\right.\)
Xét (1), đặt \(t=cosx-sinx=\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}t\in\left[-1;1\right]\\sinx.cosx=\dfrac{1-t^2}{2}\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2t+\dfrac{1-t^2}{2}=m\)
Xét hàm \(f\left(t\right)=-\dfrac{1}{2}t^2+2t+\dfrac{1}{2}\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=2\notin\left[-1;1\right]\) ; \(f\left(-1\right)=-2\) ; \(f\left(1\right)=2\)
\(\Rightarrow-2\le f\left(t\right)\le2\Rightarrow-2\le m\le2\)
Tìm điều kiện của m để các phương trình sau có nghiệm:
a) \(2sin^2x+3cos^2x=m+2\)
b) \(\frac{m-cosx}{sinx}=0\)
a/ \(2\left(1-cos^2x\right)+3cos^2x-2=m\)
\(\Leftrightarrow cos^2x=m\)
Do \(0\le cos^2x\le1\) nên pt có nghiệm khi và chỉ khi \(0\le m\le1\)
b/ \(\Leftrightarrow\left\{{}\begin{matrix}cosx=m\\sinx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx=m\\cosx\ne\pm1\end{matrix}\right.\)
\(\Rightarrow-1< m< 1\)
Bài 4:
a) Tìm m để phương trình sau có nghiệm duy nhất: 2x - mx + 2m - 1 = 0.
b) Tìm m để phương trình sau có vô số nghiệm: mx + 4 = 2x + m2.
c) Tìm m để phương trình sau có nghiệm duy nhất dương: (m2 - 4)x + m - 2 = 0
à bài này a nhớ (hay mất điểm ở bài này) ;v
xinloi cậu tớ muốn giúp lắm mà tớ ngu toán:)
a)Ta có \(2x-mx+2m-1=0\\ =>x\left(2-m\right)+2m-1=0\)
Để pt có nghiệm duy nhất thì \(a\ne0=>2-m\ne0\\=>m\ne2\)
b)Ta có \(mx+4=2x+m^2\\ =>mx+4-2x+m^2=0\\ =>\left(m-2\right)x=m^2-4\)
Để pt vô số nghiệm thì \(\left\{{}\begin{matrix}m-2=0\\m^2-4=0\end{matrix}\right.=>\left\{{}\begin{matrix}m=2\\m=\pm2\end{matrix}\right.\)\(=>m=2\)
c)Để pt có nghiệm duy nhất thì \(m^2-4\ne0>m\ne\pm2\)
Chắc vậy :v
Tìm m để phương trình cos2x+2(m+1)sinx-2m-1=0 có đúng 3 nghiệm xϵ (0;π)
A. 0≤ m< 1.
B. -1< m< 1
C. 0< m≤1
D. 0< m< 1.
Tìm m để phương trình 2sin2x – ( 2m+1) . sinx+ m = 0 có nghiệm x ∈ - π 2 ; 0
A. – 1< m < 0
B. 1< m< 2
C. – 1< m< 0
D. 0< m< 1
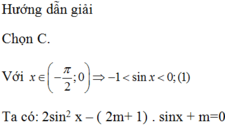
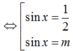
Phương trình sinx = 1/2 không có nghiệm x ∈ - π 2 ; 0
Nên để phương trình đã cho có nghiệm x ∈ - π 2 ; 0 khi và chỉ khi phương trình sinx = m có nghiệm trên khoảng đó. Kết hợp với (*) suy ra -1< m< 0
Tìm m để phương trình 2sin2x – (2m + 1)sinx + m = 0 có nghiệm x ∈ ( - π 2 ; 0).
A. -1 < m
B. 1 < m
C. -1 < m < 0
D. 0 < m < 1
Cho phương trình \(x^2-2x+m=0\)
a) tìm m để phương trình có nghiệm là 3? Tìm nghiệm còn lại
b) Tìm m để phương trình có nghiệm kép?
c) Tìm m để phương trình có 2 nghiệm phân biệt?
Tìm m để phương trình sau có 5 nghiệm phân biệt thuộc khoảng \(\left(-\dfrac{\pi}{2};3\pi\right)\)
2sin2x - (5m + 1)sinx + 2m2 + 2m = 0
Từ đường tròn lượng giác, trên \(\left(-\dfrac{\pi}{2};3\pi\right)\):
- Nếu \(0< t< 1\) thì \(sinx=t\) có 4 nghiệm
- Nếu \(-1< t< 0\) thì \(sinx=t\) có 3 nghiệm
- Nếu \(t=0\) thì \(sinx=t\) có 3 nghiệm
- Nếu \(t=1\) thì \(sinx=t\) có 2 nghiệm
- Nếu \(t=-1\) thì \(sinx=t\) có 1 nghiệm
Do đó pt đã cho có 5 nghiệm pb trong khoảng đã cho khi:
\(2t^2-\left(5m+1\right)t+2m^2+2m=0\) có 2 nghiệm pb thỏa mãn:
- TH1: \(\left\{{}\begin{matrix}t_1=-1\\0< t_2< 1\end{matrix}\right.\)
- TH2: \(\left\{{}\begin{matrix}-1< 0< t_1\\t_2=1\end{matrix}\right.\)
- TH3: \(\left\{{}\begin{matrix}t_1=0\\t_2=1\end{matrix}\right.\)
Về cơ bản, chỉ cần thay 1 nghiệm bằng 0 hoặc 1 rồi kiểm tra nghiệm còn lại có thỏa hay ko là được