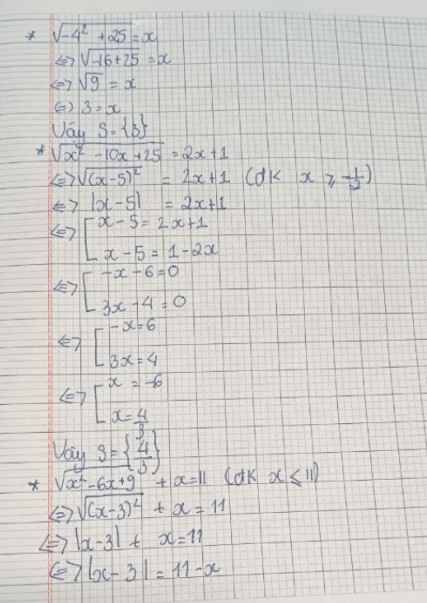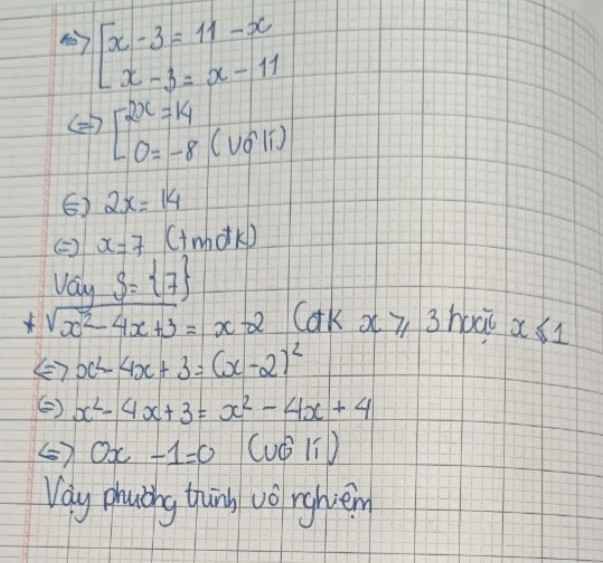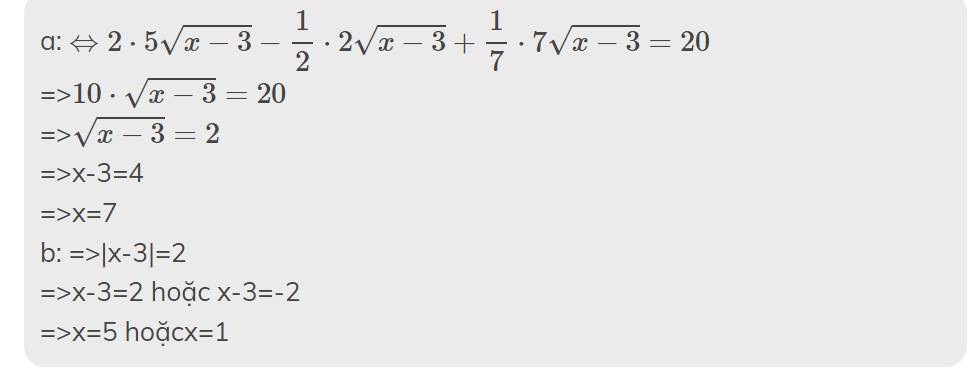11-\(\sqrt{x^2-6x+9}=\sqrt{25}\)

Những câu hỏi liên quan
Bài tập:Giải các phương trình sau
1)\(\sqrt{-4^2+25}=x\)
2)\(\sqrt{x^2-10x+25}\)=2x+1
3)\(\sqrt{x^2-6x+9}+x=11\)
4)\(\sqrt{x^2-4x+3}=x-2\)
a) \(\sqrt{4x^2-4x+1}=3\)
b)\(\sqrt{x^2-10x+25}+2-x\)
c)\(\sqrt{x^2-6x+9}+x=11\)
d)\(\sqrt{3x+19}=x+3\)
e)\(\sqrt{x^2+x+5}-1=x\)
a: =>|2x-1|=3
=>2x-1=3 hoặc 2x-1=-3
=>2x=-2 hoặc 2x=4
=>x=2 hoặc x=-1
c: \(\Leftrightarrow\left|x-3\right|=11-x\)
=>x<=11 và (x-3)^2=(11-x)^2
=>x<=11 và x^2-6x+9=x^2-22x+121
=>x<=11 và 16x=112
=>x=7
d:
ĐKXĐ: 3x+19>=0
=>x>=-19/3
PT =>x>=-3 và (3x+19)=(x+3)^2=x^2+6x+9
=>x>=-3 và x^2+6x+9-3x-19=0
=>x>=-3 và (x+5)(x-2)=0
=>x=2
e: =>\(\sqrt{x^2+x+5}=x+1\)
=>x>=-1 và x^2+x+5=x^2+2x+1
=>x>=-1 và 2x+1=x+5
=>x=4
Đúng 0
Bình luận (0)
-tìm x-
1, \(\sqrt{4-4x+x^2}=3\)
2, \(\sqrt{x^2-6x+9}=1\)
3, \(\sqrt{25-10x+x^2}=1\)
1, \(\sqrt{4-4x+x^2}=3\)
\(\Leftrightarrow\sqrt{\left(2+x\right)^2}=3\)
\(\Leftrightarrow\left|2+x\right|=3\)
TH1: \(\left|2-x\right|=2-x\) với \(2-x\ge0\Leftrightarrow x\le2\)
Pt trở thành:
\(2-x=3\) (ĐK: \(x\le2\) )
\(\Leftrightarrow x=2-3\)
\(\Leftrightarrow x=-1\left(tm\right)\)
TH2: \(\left|2-x\right|=-\left(2-x\right)\) với \(2-x< 0\Leftrightarrow x>2\)
Pt trở thành:
\(-\left(2-x\right)=3\) (ĐK: \(x>2\))
\(\Leftrightarrow-2+x=3\)
\(\Leftrightarrow x=3+2\)
\(\Leftrightarrow x=5\left(tm\right)\)
Vậy \(S=\left\{-1;5\right\}\)
Đúng 2
Bình luận (2)
2, \(\sqrt{x^2-6x+9}=1\)
\(\Leftrightarrow\sqrt{x^2-2\cdot3\cdot x+3^2}=1\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=1\)
\(\Leftrightarrow\left|x-3\right|=1\)
TH1: \(\left|x-3\right|=x-3\) với \(x-3\ge0\Leftrightarrow x\ge3\)
Pt trở thành:
\(x-3=1\) (ĐK: \(x\ge3\))
\(\Leftrightarrow x=1+3\)
\(\Leftrightarrow x=4\left(tm\right)\)
TH2: \(\left|x-3\right|=-\left(x-3\right)\) với \(x-3< 0\Leftrightarrow x< 3\)
Pt trở thành:
\(-\left(x-3\right)=1\) (ĐK: \(x< 3\))
\(\Leftrightarrow-x+3=1\)
\(\Leftrightarrow-x=1-3\)
\(\Leftrightarrow-x=-2\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy \(S=\left\{2;4\right\}\)
Đúng 0
Bình luận (0)
1) √(4 - 4x + x²) = 3
⇔ √(2 - x)² = 3
ĐKXĐ: Với mọi x ∈ R
⇔ |2 - x| = 3 (1)
*) |2 - x| = 2 - x ⇔ 2 - x ≥ 0 ⇔ x ≥ 2
(1) ⇔ 2 - x = 3
⇔ x = 2 - 3
⇔ x = -1 (nhận)
*) |2 - x| = x - 2 ⇔ 2 - x < 0 ⇔ x > 2
(1) ⇔ x - 2 = 3
⇔ x = 5 (nhận)
Vậy x = -1; x = 5
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
a) 2sqrt(25(x - 3)) - 1/2 * sqrt(4x - 12) + 1/7 * sqrt(49(x - 3)) = 20 b) sqrt(x ^ 2 - 6x + 9) = 2
Giải PT:
a) \(\sqrt{11+6\sqrt{2}}\) = \(\sqrt{2x^2-6x\sqrt{2}+9}\)
b) \(\sqrt{4x^2+4x\sqrt{7}+7}\) - \(\sqrt{8-2\sqrt{7}}\) = 0
c) \(\sqrt{x^2}\) = x
d) \(\sqrt{x^2-2x+1}\) = x-1
c: Ta có: \(\sqrt{x^2}=x\)
\(\Leftrightarrow\left|x\right|=x\)
hay \(x\ge0\)
d: Ta có: \(\sqrt{x^2-2x+1}=x-1\)
\(\Leftrightarrow\left|x-1\right|=x-1\)
hay \(x\ge1\)
Đúng 0
Bình luận (0)
Tất cả đều có điều kiện \(x\ge0\)
a,\(\sqrt{x^2-6x+9}+x=11\)
b,\(\sqrt{3x^2-4x+3=1-2x}\)
c,\(\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}=4\)
d,\(\sqrt{9x+9}+\sqrt{4x+4}=\sqrt{x+1}\)
Đề yc giải pt à em?
Đúng 0
Bình luận (0)
Câu b bạn có bị lỗi dấu căn không mà sao nó kéo dài cả 2 vế pt vậy :v
\(a,\sqrt{x^2-6x+9}+x=11\\ \Leftrightarrow\sqrt{\left(x-3\right)^2}=11-x\)
\(\Leftrightarrow\left|x-3\right|=11-x\\ TH_1:x\ge3\\ x-3=11-x\\ \Leftrightarrow2x=14\\ \Leftrightarrow x=7\left(tm\right)\)
\(TH_2:x< 3\\ -x+3=11-x\\ \Leftrightarrow-x+x=11-3\\ \Leftrightarrow0=8\left(VL\right)\)
Vậy \(S=\left\{7\right\}\)
\(c,\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}=4\) \(\left(dk:x\ge-1\right)\)
\(\Leftrightarrow\sqrt{4^2}.\sqrt{\left(x+1\right)}-\sqrt{3^2}.\sqrt{\left(x+1\right)}=4\left(1\right)\)
Đặt \(a=\sqrt{x+1}\left(a\ge0\right)\)
Pt trở thành : \(4a-3a=4\Leftrightarrow a=4\left(tmdk\right)\)
\(\Rightarrow\sqrt{x+1}=4\\ \Rightarrow\left(\sqrt{x+1}\right)^2=16\\ \Rightarrow\left|x+1\right|=16\)
\(TH_1:x\ge-1\\ x+1=16\Leftrightarrow x=15\left(tm\right)\\ TH_2:x< -1\\ -x-1=16\Leftrightarrow x=-17\left(tm\right)\)
Nhưng loại TH2 vì dk ban đầu là \(x\ge-1\)
Vậy \(S=\left\{15\right\}\)
\(d,\sqrt{9x+9}+\sqrt{4x+4}=\sqrt{x+1}\left(dk:x\ge-1\right)\\ \Leftrightarrow\sqrt{9}.\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}-\sqrt{x+1}=0\)
Đặt \(\sqrt{x+1}=a\left(a\ge0\right)\)
Tới đây bạn làm tương tự câu c nha.
Đúng 1
Bình luận (0)
Rút gọn các biểu thức sau ;
E = \(\dfrac{\left|x-3\right|}{x^2-9}.\left(x^2+6x+9\right)\)
F = \(\dfrac{\sqrt{x}}{\sqrt{x}-5}-\dfrac{10\sqrt{x}}{x-25}-\dfrac{5}{\sqrt{x}+5}\)
\(E=\dfrac{\left|x-3\right|}{\left(x-3\right)\left(x+3\right)}\left(x+3\right)^2=\dfrac{\left|x-3\right|\left(x+3\right)}{x-3}\left(x\ne\pm3\right)\)
Với \(x>3\Leftrightarrow E=x+3\)
Với \(x< 3\Leftrightarrow E=-x-3\)
\(F=\dfrac{x+5\sqrt{x}-10\sqrt{x}-5\sqrt{x}+25}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\left(x\ge0;x\ne25\right)\\ F=\dfrac{\left(\sqrt{x}-5\right)^2}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}=\dfrac{\sqrt{x}-5}{\sqrt{x}+5}\)
Đúng 2
Bình luận (0)
Giải phương trình: \(\sqrt{x^2+6x+9}+\sqrt{x^2+8x+16}+\sqrt{x^2+10x+25}=9x\)
=>\(\sqrt{\left(x+3\right)^2}\)+ \(\sqrt{\left(x+4\right)^2}\)+\(\sqrt{\left(x+5\right)^2}\)=9x
=> x + 3 + x + 4 + x + 5 = 9x
=> - 6x = - 12
=> x=2
Đúng 0
Bình luận (0)
Ủa sao phá đc trị tuyệt đối hay v bạn? (căn a^2 = trị tuyệt đối của a )
Đúng 0
Bình luận (0)
Vì \(\sqrt{x^2+6x+9}>0\\ \)
\(\sqrt{x^2+8x+16}>0\\ \)
\(\sqrt{x^2+10x+25}>0\\ \)
Suy ra 9x>0. Suy ra x>0 .Nha bạn!
Đúng 0
Bình luận (0)
2: Giải phương trình a) 2sqrt(25(x - 3)) - 1/2 * sqrt(4x - 12) + 1/7 * sqrt(49(x - 3)) = 20 b) sqrt(x ^ 2 - 6x + 9) = 2
a: \(\Leftrightarrow2\cdot5\sqrt{x-3}-\dfrac{1}{2}\cdot2\sqrt{x-3}+\dfrac{1}{7}\cdot7\sqrt{x-3}=20\)
=>\(10\cdot\sqrt{x-3}=20\)
=>\(\sqrt{x-3}=2\)
=>x-3=4
=>x=7
b: =>|x-3|=2
=>x-3=2 hoặc x-3=-2
=>x=5 hoặcx=1
Đúng 1
Bình luận (0)