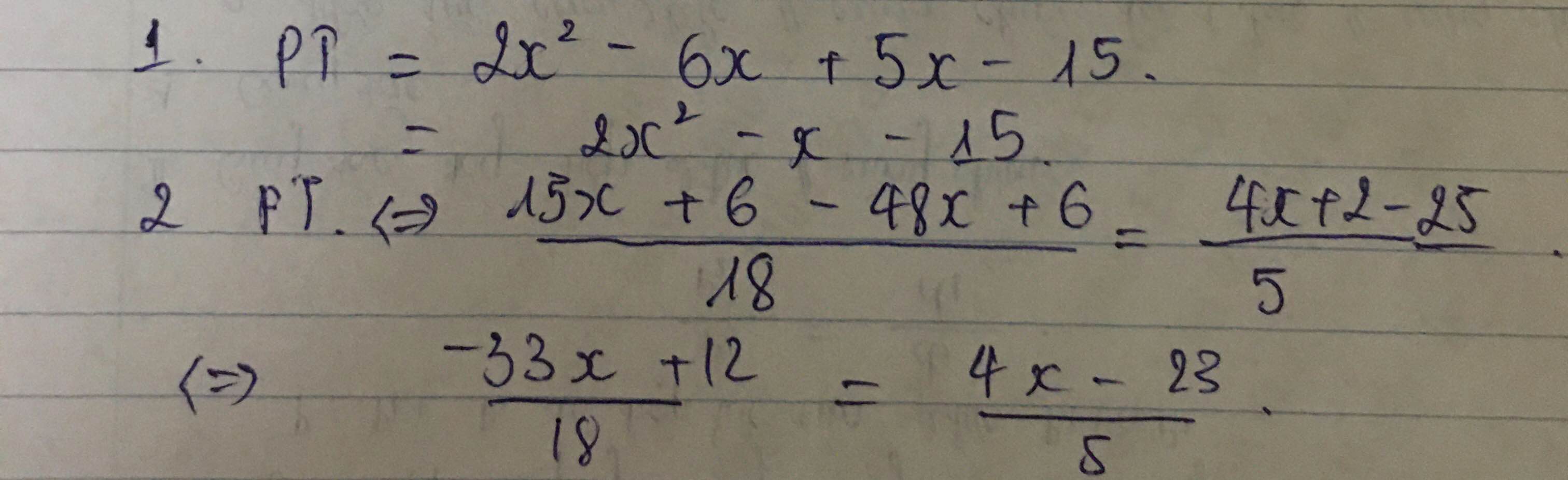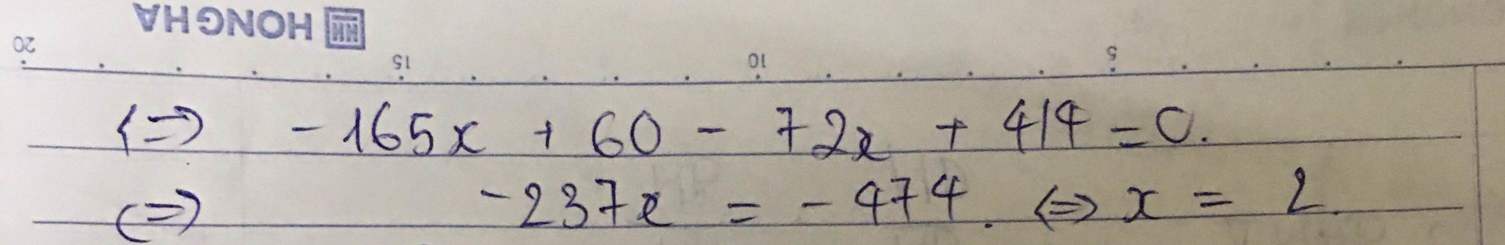bạn tải ảnh về r up lại đi bạn

\(a,4\left(x-3\right)^2-\left(2x-1\right)^2\ge12\)

\(\Leftrightarrow4x^2-24x+36-4x^2-4x+1\ge12\)

\(\Leftrightarrow-28x+37\ge12\)

\(\Leftrightarrow-28x\ge12-37\)

\(\Leftrightarrow-28x\ge-25\)

\(\Leftrightarrow x\le\dfrac{25}{28}\)

Vậy \(S=\left\{x\left|x\le\dfrac{25}{28}\right|\right\}\)

b, \(\left(x-4\right)\left(x+4\right)\ge\left(x+3\right)^2+5\)

\(\Leftrightarrow x^2-16\ge x^2+6x+9+5\)

\(\Leftrightarrow x^2-x^2-6x\ge9+5+16\)

\(\Leftrightarrow-6x\ge30\)

\(\Leftrightarrow x\le-5\)

Vậy \(S=\left\{x\left|x\le-5\right|\right\}\)

\(c,\left(3x-1\right)^2-9\left(x+2\right)\left(x-2\right)< 5x\)

\(\Leftrightarrow9x^2-6x-1-9x^2+36< 5x\)

\(\Leftrightarrow9x^2-9x^2-6x-5x+36+1< 0\)

\(\Leftrightarrow-11x+37< 0\)

\(\Leftrightarrow-11x< -37\)

\(\Leftrightarrow x>\dfrac{37}{11}\)

vậy \(S=\left\{x\left|x>\dfrac{37}{11}\right|\right\}\)

a:

ĐKXĐ: \(x\notin\left\{\dfrac{3}{2};1\right\}\)

 \(y=\dfrac{\left(x-2\right)^2}{\left(2x-3\right)\left(x-1\right)}=\dfrac{x^2-4x+4}{2x^2-2x-3x+3}\)

=>\(y=\dfrac{x^2-4x+4}{2x^2-5x+3}\)

=>\(y'=\dfrac{\left(x^2-4x+4\right)'\left(2x^2-5x+3\right)-\left(x^2-4x+4\right)\left(2x^2-5x+3\right)'}{\left(2x^2-5x+3\right)^2}\)

=>\(y'=\dfrac{\left(2x-4\right)\left(2x^2-5x+3\right)-\left(2x-5\right)\left(x^2-4x+4\right)}{\left(2x^2-5x+3\right)^2}\)

=>\(y'=\dfrac{4x^3-10x^2+6x-8x^2+20x-12-2x^3+8x^2-8x+5x^2-20x+20}{\left(2x^2-5x+3\right)^2}\)

=>\(y'=\dfrac{2x^3-5x^2-2x+8}{\left(2x^2-5x+3\right)^2}\)

b:

ĐKXĐ: x<>-3

 \(y=\left(x+3\right)+\dfrac{4}{x+3}\)

=>\(y'=\left(x+3+\dfrac{4}{x+3}\right)'=1+\left(\dfrac{4}{x+3}\right)'\)

\(=1+\dfrac{4'\left(x+3\right)-4\left(x+3\right)'}{\left(x+3\right)^2}\)

=>\(y'=1+\dfrac{-4}{\left(x+3\right)^2}=\dfrac{\left(x+3\right)^2-4}{\left(x+3\right)^2}\)

y'=0

=>\(\left(x+3\right)^2-4=0\)

=>\(\left(x+3+2\right)\left(x+3-2\right)=0\)

=>(x+5)(x+1)=0

=>x=-5 hoặc x=-1

c:

ĐKXĐ: x<>-2

 \(y=\dfrac{\left(5x-1\right)\left(x+1\right)}{x+2}\)

=>\(y=\dfrac{5x^2+5x-x-1}{x+2}=\dfrac{5x^2+4x-1}{x+2}\)

=>\(y'=\dfrac{\left(5x^2+4x-1\right)'\left(x+2\right)-\left(5x^2+4x-1\right)\left(x+2\right)'}{\left(x+2\right)^2}\)

=>\(y'=\dfrac{\left(5x+4\right)\left(x+2\right)-\left(5x^2+4x-1\right)}{\left(x+2\right)^2}\)

=>\(y'=\dfrac{5x^2+10x+4x+8-5x^2-4x+1}{\left(x+2\right)^2}\)

=>\(y'=\dfrac{10x+9}{\left(x+2\right)^2}\)

\(y'\left(-1\right)=\dfrac{10\cdot\left(-1\right)+9}{\left(-1+2\right)^2}=\dfrac{-1}{1}=-1\)

d: 

ĐKXĐ: x<>2

\(y=x-2+\dfrac{9}{x-2}\)

=>\(y'=\left(x-2+\dfrac{9}{x-2}\right)'=1+\left(\dfrac{9}{x-2}\right)'\)

\(=1+\dfrac{9'\left(x-2\right)-9\left(x-2\right)'}{\left(x-2\right)^2}\)

=>\(y'=1+\dfrac{-9}{\left(x-2\right)^2}=\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}\)

y'=0

=>\(\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}=0\)

=>\(\left(x-2\right)^2-9=0\)

=>(x-2-3)(x-2+3)=0

=>(x-5)(x+1)=0

=>x=5 hoặc x=-1

`(x^2-x+1)^4+4x^4=5x^2(x^2-x+1)^2`

Đặt `a=(x^2-x+1)^2,b=x^2`

`pt<=>a^2+4b^2=5ab`

`<=>a^2-5ab+4b^2=0`

`<=>a^2-ab-4ab+4b^2=0`

`<=>a(a-b)-4b(a-b)=0`

`<=>(a-b)(a-4b)=0`

`<=>` $\left[ \begin{array}{l}a=b\\a=4b\end{array} \right.$

`+)a=b`

`<=>x^2=(x^2-x+1)^2`

`<=>(x^2+1)(x^2-2x+1)=0`

`<=>(x-1)^2=0` do `x^2+1>0`

`<=>x=1`

`+)a=4b`

`<=>x^2=4(x^2-x+1)^2`

`<=>x^2=(2x^2-2x+1)^2`

`<=>(2x^2-x+1)(2x^2-3x+1)=0`

`+)2x^2-x+1=0`

`<=>x^2-1/2x+1/2=0`

`<=>(x-1/4)^2+7/16=0` vô lý

`+)2x^2-3x+1=0`

`<=>2x^2-2x-x+1=0`

`<=>2x(x-1)-(x-1)=0`

`<=>(x-1)(2x-1)=0`

`<=>` $\left[ \begin{array}{l}x=1\\x=\dfrac{1}{2}\end{array} \right.$

Vậy `S={1,1/2}`

b)

ĐKXĐ: \(x\notin\left\{2;3;\dfrac{1}{2}\right\}\)

Ta có: \(\dfrac{x+4}{2x^2-5x+2}+\dfrac{x+1}{2x^2-7x+3}=\dfrac{2x+5}{2x^2-7x+3}\)

\(\Leftrightarrow\dfrac{x+4}{\left(x-2\right)\left(2x-1\right)}+\dfrac{x+1}{\left(x-3\right)\left(2x-1\right)}=\dfrac{2x+5}{\left(2x-1\right)\left(x-3\right)}\)

\(\Leftrightarrow\dfrac{\left(x+4\right)\left(x-3\right)}{\left(x-2\right)\left(2x-1\right)\left(x-3\right)}+\dfrac{\left(x+1\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1\right)}=\dfrac{\left(2x+5\right)\left(x-2\right)}{\left(2x-1\right)\left(x-3\right)\left(x-2\right)}\)

Suy ra: \(x^2-3x+4x-12+x^2-2x+x-2=2x^2-4x+5x-10\)

\(\Leftrightarrow2x^2-14=2x^2+x-10\)

\(\Leftrightarrow2x^2-14-2x^2-x+10=0\)

\(\Leftrightarrow-x-4=0\)

\(\Leftrightarrow-x=4\)

hay x=-4(nhận)

Vậy: S={-4}

\(1,\) thiếu đề

\(2,\dfrac{5x+2}{6}-\dfrac{8x-1}{3}=\dfrac{4x+2}{5}-5\)

\(\Leftrightarrow\dfrac{5\left(5x+2\right)}{30}-\dfrac{10\left(8x-1\right)}{30}=\dfrac{6\left(4x+2\right)}{30}-\dfrac{150}{30}\)

\(\Leftrightarrow5\left(5x+2\right)-10\left(8x-1\right)=6\left(4x+2\right)-150\)

\(\Leftrightarrow25x+10-80x+10=24x+12-150\)

\(\Leftrightarrow-55x+20=24x-138\)

\(\Leftrightarrow24x-138+55x-20=0\)

\(\Leftrightarrow79x-158=0\)

\(\Leftrightarrow x=2\)

\(3,ĐKXĐ:\left\{{}\begin{matrix}x\ne1\\x\ne-1\\x\ne3\end{matrix}\right.\\ \dfrac{x}{2x-6}+\dfrac{x}{2x-2}=\dfrac{-2x}{\left(x+1\right)\left(3-x\right)}\)

\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}+\dfrac{2x}{\left(x+1\right)\left(3-x\right)}=0\)

\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}-\dfrac{2x}{\left(x+1\right)\left(x-3\right)}=0\)

\(\Leftrightarrow x\left(\dfrac{1}{2\left(x-3\right)}+\dfrac{1}{2\left(x-1\right)}-\dfrac{2}{\left(x+1\right)\left(x-3\right)}\right)=0\)

\(\Leftrightarrow x\left(\dfrac{\left(x-1\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4\left(x-1\right)}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)

\(\Leftrightarrow x\left(\dfrac{x^2-1}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{x^2-2x-3}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4x-4}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)

\(\Leftrightarrow x.\dfrac{x^2-1+x^2-2x-3-4x+4}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x.\dfrac{2x^2-6x}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x.\dfrac{2x\left(x-3\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x.\dfrac{x}{\left(x-1\right)\left(x+1\right)}=0\)

\(\Leftrightarrow\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x=0\)

\(x^2+5x+4-3\sqrt{x^2+5x+2}=6\)

\(x^2+5x+2+2-3\sqrt{x^2+5x+2}=6\)

Đặt  \(t=\sqrt{x^2+5x+2}\)  (t >= 0)

=>  t² - 3t - 4 = 0 => t1 = -1 (loại) và t2 = 4

=> \(\sqrt{x^2+5x+2}=4\)

\(x^2+5x+2=16\)

\(x^2+5x-14=0\)

x1=-7; x2 = 2

(x²-5x+1)(x²-4)=6(x-1)²

<=>(x²-5x+1)(x²-4)-6(x-1)²=0

<=>x⁴-5x³-3x²+20x-4-6x²+12x-6=0

<=>x⁴-5x³-9x²+32x-10=0

<=>x⁴-6x³+2x²+x³-6x²+2x-5x²+30x-10=0

<=>x²(x²-6x+2)+x(x²-6x+2)-5(x²-6x+2)=0

<=>(x²-6x+2)(x²+x-5)=0

<=>(x-3)²-7=0

\(\Leftrightarrow x-3=-\sqrt{7}hoac\sqrt{7}\)

\(\Leftrightarrow3\pm\sqrt{7}\)

\(\Leftrightarrow\left(x+\frac{1}{2}\right)^2=\frac{21}{4}\)

\(\Leftrightarrow x=-\frac{1}{2}-\frac{\sqrt{21}}{2}hoac\frac{\sqrt{21}}{2}-\frac{1}{2}\)

b)\(x+\frac{1}{x}=x^2+\frac{1}{x^2}\)

tính mẫu ra rồi rút gọn,x=1

 \(1,\dfrac{5x-1}{3}-1=2x+3\\ \Leftrightarrow\dfrac{5x-4}{3}=2x+3\\ \Leftrightarrow5x-4=3\left(2x+3\right)\\ \Leftrightarrow5x-4=6x+9\\ \Leftrightarrow6x+9-5x+4=0\\ \Leftrightarrow x+13=0\\ \Leftrightarrow x=-13\)

\(2,16x^2-3=\left(4x-3\right)\left(5x+1\right)\\ \Leftrightarrow16x^2-3=20x^2-15x+4x-3\\ \Leftrightarrow16x^2-3=20x^2-11x-3\\ \Leftrightarrow20x^2-11x-3-16x^2+3=0\\ \Leftrightarrow4x^2-11x=0\\ \Leftrightarrow x\left(4x-11\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{11}{4}\end{matrix}\right.\)

\(3,ĐKXĐ:x\ne\pm2\\ \dfrac{x-2}{x+2}-\dfrac{3}{x-2}=\dfrac{-x\left(15-x\right)}{x^2-4}\\ \Leftrightarrow\dfrac{\left(x-2\right)^2-3\left(x+2\right)}{x^2-4}=\dfrac{x^2-15x}{x^2-4}\\ \Leftrightarrow\left(x-2\right)^2-3\left(x+2\right)=x^2-15x\)

\(\Leftrightarrow x^2-4x+4-3x-6-x^2+15x=0\\ \Leftrightarrow8x-2=0\\ \Leftrightarrow x=\dfrac{1}{4}\left(tm\right)\)

ĐKXĐ: \(x\notin\left\{-1;-2;-3;-4\right\}\)

Ta có: \(\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}=\dfrac{1}{6}\)

\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}=\dfrac{1}{6}\)

\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+4}=\dfrac{1}{6}\)

\(\Leftrightarrow\dfrac{x+4}{\left(x+1\right)\left(x+4\right)}-\dfrac{x+1}{\left(x+1\right)\left(x+4\right)}=\dfrac{1}{6}\)

\(\Leftrightarrow\dfrac{x+4-x-1}{\left(x+1\right)\left(x+4\right)}=\dfrac{x^2+5x+4}{6\left(x+1\right)\left(x+4\right)}\)

\(\Leftrightarrow\dfrac{18}{6\left(x+1\right)\left(x+4\right)}=\dfrac{x^2+5x+4}{6\left(x+1\right)\left(x+4\right)}\)

Suy ra: \(x^2+5x+4=18\)

\(\Leftrightarrow x^2+5x-14=0\)

\(\Leftrightarrow x^2+7x-2x-14=0\)

\(\Leftrightarrow x\left(x+7\right)-2\left(x+7\right)=0\)

\(\Leftrightarrow\left(x+7\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+7=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-7\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)

Vậy: S={-7;2}

ĐKXĐ: $x \neq -1;-2;-3;-4$

$pt⇔\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}=\dfrac{1}{6}$

$⇔\dfrac{1}{x+1}-\dfrac{1}{x+4}=\dfrac{1}{6}$

$⇔\dfrac{3}{(x+1)(x+4)}=\dfrac{1}{6}$

$⇔x^2+5x+4=18$

$⇔x^2+5x-14=0$

$⇔(x-2)(x+7)=0$

$⇔$ \(\left[{}\begin{matrix}x=2\\x=-7\end{matrix}\right.\)(t/m)

Vậy...