Chứng minh rằng nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân.

Những câu hỏi liên quan
1) chứng minh định lý: nếu một tam giác có hai góc ở đấy bằng nhau thì tam giác đó là tam giác cân
2) chứng minh định lý: nếu một tam giác cân có một góc bằng 600 thì tam giác đó là tam giác đều
chứng minh rằng nếu 1 tam giác có 2 trung tuyến bằng nhau thì đó là tam giác cân
giả sử tam giác ABC có 2 đường trung tuyến BM và CN gặp nhau ở G
=> G là trong tâm của tam giác
-> GB=BM ; GC = CN
mà BM=CN (gt) nên GB = GC
=> tam giác GBC cân tại G
Do đó tam giác BCN=tam giác CBM vì:
BC là cạnh chung
CN = BM (gt)
=> tam giác ABC cân tại A
Đúng 1
Bình luận (0)
Chứng minh rằng nếu 1 tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân
Gọi tam giác đề bài cho là ΔABC có BD,CE là các trung tuyến, BD=CE. Cần chứng minh ΔABC cân tại A
Gọi G là giao điểm của BD và CE
Xét ΔABC có
BD,CE là trung tuyến
BD cắt CE tại G
=>G là trọng tâm
=>GB=2/3BD và GC=2/3CE
mà BD=CE
nên GB=GC
=>góc GBC=góc GCB
Xét ΔDBC và ΔECB có
BC chung
góc DBC=góc ECB
DB=EC
=>ΔDBC=ΔECB
=>góc DCB=góc EBC
=>ΔABC cân tại A
Đúng 0
Bình luận (0)
Bài 1 Các câu sau đúng Đ hay sai S 1 Tam giác có 2 góc bằng 45° là tam giác vuông cân.2 Hai tam giác có 2 cặp góc tương ứng bằng nhau thì cặp góc còn lại cũng tương ứng bằngnhau3 Hai tam giác có 2 cặp cạnh tương ứng bằng nhau thì cặp cạnh còn lại cũng tương ứngbăng nhau4 Nếu 1 cạnh góc vuông và 1 góc nhọn của tam giác vuông này bằng 1 cạnh góc vuông vàgóc nhọn của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau.5 Tam giác cân có 1 góc bằng 60° là tam giác đều.6 Tạm giác cân có 1 góc bằng 45...
Đọc tiếp
Bài 1 Các câu sau đúng Đ hay sai S 1 Tam giác có 2 góc bằng 45° là tam giác vuông cân.2 Hai tam giác có 2 cặp góc tương ứng bằng nhau thì cặp góc còn lại cũng tương ứng bằngnhau3 Hai tam giác có 2 cặp cạnh tương ứng bằng nhau thì cặp cạnh còn lại cũng tương ứngbăng nhau4 Nếu 1 cạnh góc vuông và 1 góc nhọn của tam giác vuông này bằng 1 cạnh góc vuông vàgóc nhọn của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau.5 Tam giác cân có 1 góc bằng 60° là tam giác đều.6 Tạm giác cân có 1 góc bằng 45° là tam giác vuông cân.7 Nếu tam giác có độ dài 3 cạnh lần lượt là 3,4,5 thì tam giác đó là tam giác vuông.8 Hai tam giác đều thì bằng nhau.9 Góc ngoài của tam giác luôn lớn hơn mỗi góc trong của tam giác đó.10 Trong tam giác cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực củacạnh đáy.11 Nếu cạnh huyền của tam giác vuông cân này bằng cạnh huyền của tam giác vuông cânkia thì 2 tam giác đó bằng nhau .12 Tam giác ABC vuông tại A, M là trung điểm của đoạn thắng BC. Nếu AB 2 cm, AC 51 cm thì AM 2 cm.13 Tam giác ABC vuông tại A, M là trung điểm của BC. Nếu 2B 30° và AM 6 cm, thìAC 6cm.14 Nếu 2 tam giác cân có 2 cặp cạnh bên bằng nhau thì 2 tam giác cân đó bằng nhau.15 Nếu cạnh bên và cạnh đáy của tam giác cân này bằng cạnh bên và cạnh đáy của tam giáccân kia thì 2 tam giác cân bằng nhau.16 Nếu 2 tam giác cân có chung góc ở đỉnh thì 2 cạnh đáy của chúng song song với nhau.17 Nếu 2 cạnh và 1 góc của tam giác này lần lượt bằng 2 cạnh và 1 góc của tam giác kia thì2 tam giác đó bằng nhau.18 Nếu 3 tam giác cân AMN , BMN , CMN cùng chung cạnh đáy MN thì 3 điểm A, B, Cthắng hàng.19 Nếu 2 tam giác vuông cân có 1 cặp cạnh góc vuông bằng nhau thì chúng bằng nhau.20 Trong tam giác cân các góc đều có thể là góc nhọn hoặc góc tù.
Chứng minh rằng nếu một tam giác có hai trung tuyến bằng nhau thì tam giác đó là tam giác cân.
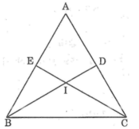
Giả sử ΔABC có hai đường trung tuyến BD và CE bằng nhau.
Gọi I là giao điểm BD và CE, ta có:
BI = 2/3 BD (tính chất đường trung tuyến) (1)
CI = 2/3 CE (tính chất đường trung tuyến) (2)
Từ (1), (2) và giả thiết BD = CE suy ra: BI = CI
Do BD = CE suy ra: BI + ID = CI + IE
Mà BI = CI ( chứng minh trên) nên : ID = IE
Xét ΔBIE và ΔCID, ta có:
BI = CI (chứng minh trên)
∠(BIE) = ∠(CID) (đối đỉnh)
IE = ID (chứng minh trên)
Suy ra: ΔBIE = ΔCID (c.g.c)
Suy ra: BE = CD (hai cạnh tương ứng) (3)
Lại có: BE = 1/2 AB (vì E là trung điểm AB) (4)
CD = 1/2 AC (vì D trung điểm AC) (5)
Từ (3), (4) và (5) suy ra: AB = AC.
Vậy tam giác ABC cân tại A.
Đúng 0
Bình luận (0)
Bài 1: Các câu sau đúng(Đ) hay sai(S):1) Tam giác có 2 góc bằng 45° là tam giác vuông cân.2) Hai tam giác có 2 cặp góc tương ứng bằng nhau thì cặp góc còn lại cũng tương ứng bằngnhau3) Hai tam giác có 2 cặp cạnh tương ứng bằng nhau thì cặp cạnh còn lại cũng tương ứngbăng nhau4) Nếu 1 cạnh góc vuông và 1 góc nhọn của tam giác vuông này bằng 1 cạnh góc vuông vàgóc nhọn của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau.5) Tam giác cân có 1 góc bằng 60° là tam giác đều.6) Tạm giác cân có 1 gó...
Đọc tiếp
Bài 1: Các câu sau đúng(Đ) hay sai(S):1) Tam giác có 2 góc bằng 45° là tam giác vuông cân.
2) Hai tam giác có 2 cặp góc tương ứng bằng nhau thì cặp góc còn lại cũng tương ứng bằngnhau
3) Hai tam giác có 2 cặp cạnh tương ứng bằng nhau thì cặp cạnh còn lại cũng tương ứngbăng nhau
4) Nếu 1 cạnh góc vuông và 1 góc nhọn của tam giác vuông này bằng 1 cạnh góc vuông vàgóc nhọn của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau.
5) Tam giác cân có 1 góc bằng 60° là tam giác đều.
6) Tạm giác cân có 1 góc bằng 45° là tam giác vuông cân
.7)Nếu tam giác có độ dài 3 cạnh lần lượt là 3,4,5 thì tam giác đó là tam giác vuông.
8) Hai tam giác đều thì bằng nhau
.9) Góc ngoài của tam giác luôn lớn hơn mỗi góc trong của tam giác đó
.10) Trong tam giác cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực củacạnh đáy.
11) Nếu cạnh huyền của tam giác vuông cân này bằng cạnh huyền của tam giác vuông cânkia thì 2 tam giác đó bằng nhau .
12) Tam giác ABC vuông tại A, M là trung điểm của đoạn thắng BC. Nếu AB = 2 cm, AC =51 cm thì AM = 2 cm.
13) Tam giác ABC vuông tại A, M là trung điểm của BC. Nếu 2B= 30° và AM = 6 cm, thìAC = 6cm
.14) Nếu 2 tam giác cân có 2 cặp cạnh bên bằng nhau thì 2 tam giác cân đó bằng nhau.
15) Nếu cạnh bên và cạnh đáy của tam giác cân này bằng cạnh bên và cạnh đáy của tam giáccân kia thì 2 tam giác cân bằng nhau.
16) Nếu 2 tam giác cân có chung góc ở đỉnh thì 2 cạnh đáy của chúng song song với nhau
.17) Nếu 2 cạnh và 1 góc của tam giác này lần lượt bằng 2 cạnh và 1 góc của tam giác kia thì2 tam giác đó bằng nhau.
18) Nếu 3 tam giác cân AMN , BMN , CMN cùng chung cạnh đáy MN thì 3 điểm A, B, Cthắng hàng.
19) Nếu 2 tam giác vuông cân có 1 cặp cạnh góc vuông bằng nhau thì chúng bằng nhau.
20) Trong tam giác cân các góc đều có thể là góc nhọn hoặc góc tù.
ĐĐSĐĐĐĐSSĐĐSĐSĐĐSĐĐS
1.Đ
2.Đ
3.S
4.Đ
5.Đ
6.S
7.Đ
8.S
9.Đ
10.Đ
11.Đ
12.S
13.S
14.S
15.S
16.Đ
17.S
18.Đ
19.Đ
20.Đ
Chứng minh rằng một tam giác có hai đường đường cao(xuất phát từ các đỉng của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> Góc FBC = góc ECB
hay ∆ABC cân tại A
Đúng 0
Bình luận (0)
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Hướng dẫn:
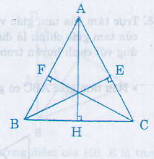
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF (giả thiết)
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> \(\widehat{FBC}=\widehat{ECB}\)
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được ba góc của chúng bằng nhau, suy ra đó là tam giác đều.
Đúng 1
Bình luận (1)

Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> ˆFBC=ˆECBFBC^=ECB^
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.
Đúng 0
Bình luận (0)
chứng minh định lý nếu một tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân
Xét ΔABC có \(\widehat{B}=\widehat{C}\)
mà cạnh đối diện của góc B là cạnh AC
và cạnh đối diện của góc C là cạnh AB
nên AB=AC
Đúng 0
Bình luận (0)
Chứng minh rằng nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân ?
Gọi Δ ABC có trung tuyến BM = CN, G là trọng tâm Δ (giao điểm các trung tuyến)
Ta có :
GB = 2/3.BM
GC = 2/3.CN
Mà BM = CN => GB = GC
=> Δ BGC cân tại G
=> ∠ MBC = ∠ NCB
Xét Δ BMC và Δ CNB :
BM = CN
∠ MBC = ∠ NCB
BC là cạnh chung
=> Δ BMC = Δ CNB (c - g - c)
=> ∠ MCB = ∠ NBC
hay ∠ ACB = ∠ ABC
=> Δ ABC cân tại A (đpcm)
Đúng 1
Bình luận (0)























