Question

Chứng minh rằng nếu một tam giác có hai trung tuyến bằng nhau thì tam giác đó là tam giác cân.

Answer 1

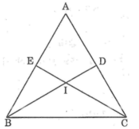
Giả sử ΔABC có hai đường trung tuyến BD và CE bằng nhau.

Gọi I là giao điểm BD và CE, ta có:

BI = 2/3 BD (tính chất đường trung tuyến) (1)

CI = 2/3 CE (tính chất đường trung tuyến) (2)

Từ (1), (2) và giả thiết BD = CE suy ra: BI = CI

Do BD = CE suy ra: BI + ID = CI + IE

Mà BI = CI ( chứng minh trên) nên : ID = IE

Xét ΔBIE và ΔCID, ta có:

BI = CI (chứng minh trên)

∠(BIE) = ∠(CID) (đối đỉnh)

IE = ID (chứng minh trên)

Suy ra: ΔBIE = ΔCID (c.g.c)

Suy ra: BE = CD (hai cạnh tương ứng) (3)

Lại có: BE = 1/2 AB (vì E là trung điểm AB) (4)

CD = 1/2 AC (vì D trung điểm AC) (5)

Từ (3), (4) và (5) suy ra: AB = AC.

Vậy tam giác ABC cân tại A.