Hướng dẫn:
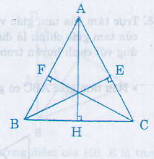
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF (giả thiết)
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> \(\widehat{FBC}=\widehat{ECB}\)
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được ba góc của chúng bằng nhau, suy ra đó là tam giác đều.

Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> ˆFBC=ˆECBFBC^=ECB^
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.









