Hãy giải thích vì sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác ?
Bài 9: Tính chất ba đường cao của tam giác
Bài 58 (SGK - tập 2 trang 83)
Thảo luận (2)
Bài 59 (SGK - tập 2 trang 83)
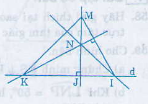
Cho hình 57 :
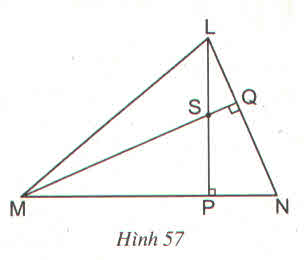
a) Chứng minh \(NS\perp LM\)
b) Khi \(\widehat{LNP}=50^0\), hãy tính góc MSP và góc PSQ
Thảo luận (3)Hướng dẫn giảia) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
(Trả lời bởi Nguyễn Thị Thảo)
Bài 60 (SGK - tập 2 trang 83)
Trên đường thẳng d, lấy 3 điểm phân biệt I, J, K (J ở giữa I và K)
Kẻ đường thẳng l vuông góc với d tại J. Trên l lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N
Chứng minh \(KM\perp IM\) ?
Thảo luận (3)Hướng dẫn giảiGiải tương tự như bài tập 59
∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK
(Trả lời bởi Trần Nguyễn Bảo Quyên)
Bài 61 (SGK - tập 2 trang 83)
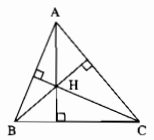
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC
Thảo luận (2)Hướng dẫn giảiCác đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E
a) ∆HBC có:
HN ⊥ BC nên HN là đường cao
BE ⊥ HC nên BE là đường cao
CM ⊥ BH nên CM là đường cao
Vậy A là trực tâm của ∆HBC
b) Tương tự trực tâm của ∆AHB là C, ∆AHC là B
(Trả lời bởi Trần Nguyễn Bảo Quyên)
Bài 62 (SGK - tập 2 trang 83)
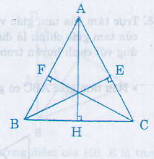
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Thảo luận (2)Hướng dẫn giảiHướng dẫn:
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF (giả thiết)
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> \(\widehat{FBC}=\widehat{ECB}\)
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được ba góc của chúng bằng nhau, suy ra đó là tam giác đều.
(Trả lời bởi Thien Tu Borum)
Bài 70 (Sách bài tập - tập 2 - trang 50)
Cho tam giác ABC vuông tại B. Điểm nào là trực tâm của tam giác đó ?
Thảo luận (1)Hướng dẫn giảiĐiểm B là trực tâm
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Bài 71 (Sách bài tập - tập 2 - trang 50)
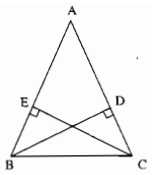
Cho hình 15 :

a) Chứng minh : \(CI\perp AB\) ?
b) Cho \(\widehat{ACB}=40^0\) . Tính \(\widehat{BID},\widehat{DIE}\) ?
Thảo luận (1)Hướng dẫn giảia) △ABC có : Hai đường cao BE và AD mà 2 đường này cùng cắt nhau tại điểm I ⇒ I là trực tâm
⇒ CI là đường cao còn lại ⇒ CI ⊥ AB
b) Xét △BEC có : góc EBC + gócBEC + góc BCE = \(180^0\)( định lí tổng ba góc )
⇒ góc EBC = \(180^0\) - góc BEC - góc BCE = \(180^0\)- \(90^0\)-\(40^0\)= \(50^0\)
Lại xét △BID có : góc BID + góc IBD + góc BDI = \(180^0\)
⇒ góc BID = \(180^0\) - \(90^0\) - \(50^0\) = \(40^0\)
Có góc BID + góc DIE = \(180^0\)( 2 góc kề bù )
⇒ góc DIE = \(180^0\) - góc BID = \(180^0-40^0\)= \(140^0\)
(Trả lời bởi Cuc Pham)
Bài 72 (Sách bài tập - tập 2 - trang 51)
Cho H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HAB, HAC, HBC ?
Thảo luận (1)Hướng dẫn giảiGiải
Trong ∆ABC ta có H là trực tâm nên
\(\text{ AH⊥BC,BH⊥AC,CH⊥AB}\)
Trong ∆AHB ta có:
\(\text{AC⊥BH }\)
\(\text{BC⊥AH}\)
Hai đường cao kẻ từ A và B cắt nhau tại C.
Vậy C là trực tâm của ∆AHB.
Trong ∆HAC ta có:
\(\text{BA⊥CH}\)
\(\text{CB⊥BH}\)
Hai đường cao kẻ từ A và C cắt nhau tại B, Vậy B là trực tâm của ∆HAC.
Trong ∆HBC ta có:
\(\text{BA⊥HC}\)
\(\text{CA⊥BH}\)
Hai đường cao kẻ từ B và C cắt nhau tại A. Vậy A là trực tâm của ∆HBC.
(Trả lời bởi Thảo Phương)
Bài 73 (Sách bài tập - tập 2 - trang 51)
Tam giác ABC có các đường cao BD và CE bằng nhau. Chứng minh rằng tam giác đó cân ?
Thảo luận (1)Hướng dẫn giải
Xét hai tam giác vuông BDC và CEB:
góc BDC= góc CEB=90∘
BD = CE (gt)
BC cạnh huyền chung
Do đó: ∆BDC = ∆CEB (cạnh huyền, cạnh góc vuông)
⇒ góc DCB= góc EBC
Hay góc ACB= góc ABC
Vậy ∆ABC cân tại A.
(Trả lời bởi Nguyễn Thị Diễm Quỳnh)
Bài 74 (Sách bài tập - tập 2 - trang 51)
Tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của các tam giác ABC, AHB, AHC ?
Thảo luận (1)Hướng dẫn giảiTrực tâm của ΔABC là đỉnh A
Trực tâm của ΔAHB là đỉnh H
Trực tâm của ΔAHC là đỉnh H
(Trả lời bởi Nguyễn Lê Phước Thịnh)