Phân tích đa thức thành nhân tử thôi bạn :

Ta có :

\(h\left(x\right)=x^2+5x+6\)

\(h\left(x\right)=x\left(x+2\right)+3\left(x+2\right)\)

\(h\left(x\right)=\left(x+2\right)\left(x+3\right)\)

\(\Rightarrow N_oh\left(x\right)=-2;-3\)

\(g\left(x\right)=2x^2+7x-9\)

\(g\left(x\right)=2x^2+9x-2x-9\)

\(g\left(x\right)=2x\left(x-1\right)+9\left(x-1\right)\)

\(g\left(x\right)=\left(x-1\right)\left(2x+9\right)\)

\(\Rightarrow N_og\left(x\right)=1;-4,5\)

ko biet

haha

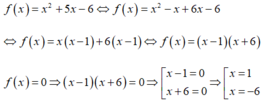
Vậy nghiệm của đa thức f(x) là 1 và -6

Chọn đáp án B

P(x) = x2 + 5x – 6

P(-6) = (-6)2 + 5.(-6) – 6 = 36 – 30 – 6 = 0

P(-1) = (-1)2 + 5.(-1) – 6 = 1 - 5 – 6 = - 10 ≠ 0

P(1) = 12 + 5.1 – 6 = 1 + 5 – 6 = 0

P(6) = 62 + 5.6 – 6 = 36 + 30 – 6 = 60 ≠ 0

Vậy -6 và 1 là nghiệm của P(x).

`x^2 - 3x = 0`

`<=> x.(x-3)=0`

`<=> x = 0` hoặc `x-3=0`

`<=> x = 0 ` hoặc `x = 3`

Vậy `S = { 0;3}`

`2x^2 + 5x = 0`

`<=> x.(2x + 5)=0`

`<=> x = 0` hoặc `2x+5=0`

`<=> x = 0` hoặc `2x= -5`

`<=> x = 0` hoặc `x = -5/2`

Vậy `S = {0; -5/2}`

\(a,x^2-3x=0\\ x\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\\ b,2x^2+5x=0\\ x\left(2x+5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\2x+5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\end{matrix}\right.\)

`x^2 -3x=0`

`=>x(x-3)=0`

\(=>\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\\ =>\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)

b)

`2x^2 +5x=0`

`=>x(2x+5)=0`

\(=>\left[{}\begin{matrix}x=0\\2x+5=0\end{matrix}\right.\\ =>\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\end{matrix}\right.\)

Đa thức f(x) = x2 – 5x + 4 có dạng ax2 + bx+ c trong đó hệ số a = 1, b = -5, c = 4

Ta có: a + b + c = 1 + (-5) + 4 = 1 – 5 + 4 = 0

Theo bài 46, vì a + b + c = 0 nên đa thức f(x) = x2 – 5x + 4 có nghiệm x = 1

A.2 và 3

f(x)=x^2+5x-6=0

     =(x^2+ 2x5/2+ 25/4)-(7/2)^2=0

=>(x+5/2)^2=(7/2)^2

TH1:x+5/2=7/2=>x=1

TH2:x+5/2=-7/2=>x=-6

Chọn A

Lời giải:

1.

$4x+9=0$

$4x=-9$

$x=\frac{-9}{4}$
2.

$-5x+6=0$

$-5x=-6$

$x=\frac{6}{5}$

3.

$x^2-1=0$

$x^2=1=1^2=(-1)^2$

$x=\pm 1$

4.

$x^2-9=0$

$x^2=9=3^2=(-3)^2$

$x=\pm 3$

5.

$x^2-x=0$

$x(x-1)=0$

$x=0$ hoặc $x-1=0$

$x=0$ hoặc $x=1$

6.

$x^2-2x=0$

$x(x-2)=0$

$x=0$ hoặc $x-2=0$

$x=0$ hoặc $x=2$

7.

$x^2-3x=0$

$x(x-3)=0$

$x=0$ hoặc $x-3=0$ 

$x=0$ hoặc $x=3$

8.

$3x^2-4x=0$

$x(3x-4)=0$

$x=0$ hoặc $3x-4=0$

$x=0$ hoặc $x=\frac{4}{3}$

sai đề rồi bn

Cái nào cũng không phải là nghiệm hết ạ;-;

c. Thay x = -1 vào A(x) và B(x) ta có:

A(-1) = 0, B(-1) = 2

Vậy x = -1 là nghiệm của A(x) nhưng không là nghiệm của B(x) (1 điểm)

c. Ta có h(x) = 0 ⇒ 5x + 1 = 0 ⇒ x = -1/5

Vậy nghiệm của đa thức h(x) là x = -1/5 (1 điểm)