Giúp em bài này với ạ, nhớ giải chi tiết hộ em, chi tiết hộ ạ :((
mng giải hộ em bài này chi tiết được k v ạ em cmon nhieeufu ạ
\(\orbr{\frac{1}{1-\sqrt{x}}-\frac{1}{\sqrt{x}}]}\div\orbr{\begin{cases}\\\end{cases}(2\sqrt{x}-1)(\frac{1}{1-\sqrt{x}}+\frac{\sqrt{x}}{1-\sqrt{x}+x})]}\)
sori mng em bị lag xíu
mọi người giải giúp em ik ạ pls em gấp lắmmm
Mn giải chi tiết hộ em câu 3 với,làm chi tiết hộ em ạ,em cảm ơn
Gọi số sản phẩm dự định là a (sản phẩm ) (a là số tự nhiên khác 0)
Vì theo dự định mỗi ngày sản xuất 50 sản phẩm nên số ngày theo dự định là \(\dfrac{a}{50}\)
Nhưng thực tế , đội đã sản xuất theeo được 30 sản phẩm do mỗi ngày vượt mức 10 sản phẩm (nghĩa là sản xuất 60 sản phẩm) , nên số ngày thực tế là \(\dfrac{a+30}{60}\)
Vì thực tế sớm hơn dự định 2 ngày nên ta có phương trình :
\(\dfrac{a}{50}=\dfrac{a+30}{60}+2\\ \Leftrightarrow6a=5\left(a+30+120\right)\\\Leftrightarrow a=750\left(t.m\right) \)
Vậy số sản phẩm dự định là 750 sản phẩm
Bài 3:
Gọi số sản phẩm đội phải sản xuất theo kế hoạch là x( sản phẩm, x\(\in N\)*)
Thời gian đội sản xuất theo kế hoạch là: \(\dfrac{x}{50}\) (ngày)
Số ngày làm thực tế là: \(\dfrac{x+30}{50+10}=\dfrac{x+30}{60}\) (ngày)
Theo bài ra, ta có phương trình:
\(\dfrac{x}{50}-\dfrac{x+30}{60}=2\)
\(\Leftrightarrow\dfrac{60x-50\left(x+30\right)}{50.60}=2\)
\(\Leftrightarrow60x-50x-1500=6000\Leftrightarrow x=750\)(thoả mãn)
Vậy theo kế hoạch đội phải sản xuất 750 sản phẩm
Ai giúp mình bài này với ạ!!! Giải chi tiết hộ mình nhé! Mình cảm ơn ạ!!!
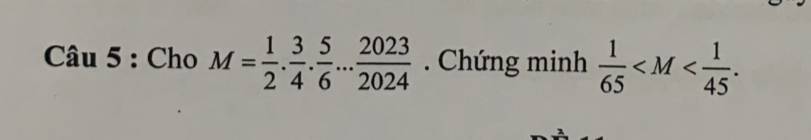
Giúp em với mn, câu c thôi ạ. Giải chi tiết (ko tắt) hộ em với ạ

a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)
\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
Giải chi tiết hộ em bài 4 ạ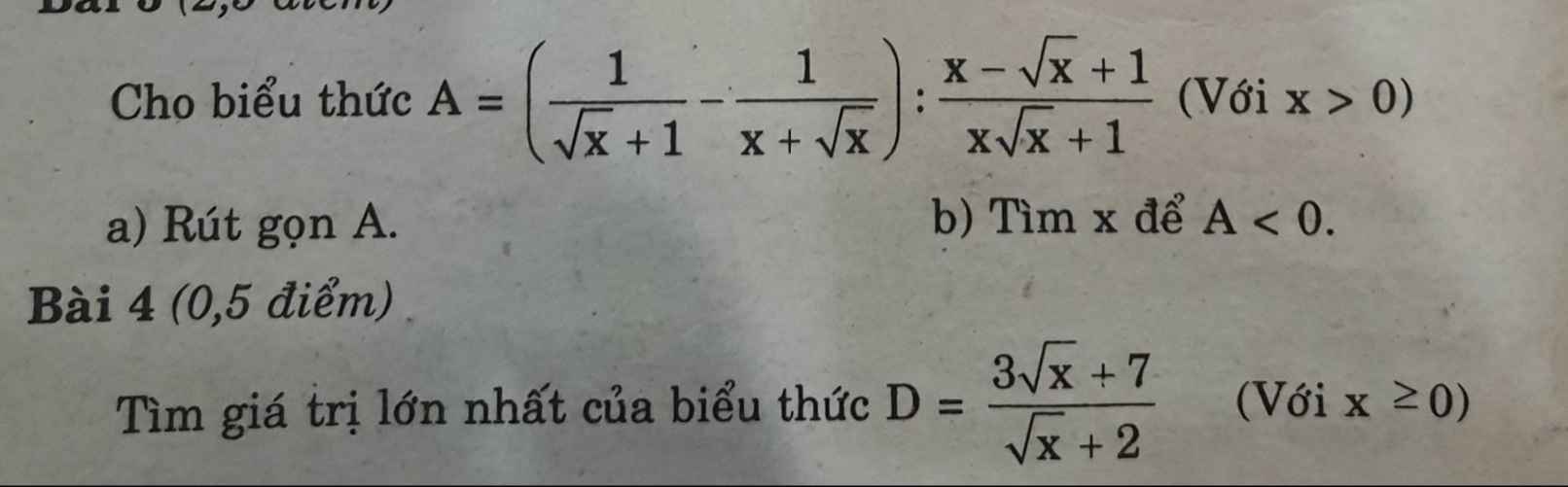
a: Ta có: \(A=\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{1}{x+\sqrt{x}}\right):\dfrac{x-\sqrt{x}+1}{x\sqrt{x}+1}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}+1}{1}\)
\(=\dfrac{x-1}{\sqrt{x}}\)
b: Để A<0 thì x-1<0
hay x<1
Kết hợp ĐKXĐ, ta được: 0<x<1
với \(x\ge0\) ta có :\(D=\dfrac{3\sqrt{x+7}}{\sqrt{x}+2}=\dfrac{3\left(\sqrt{x}+2\right)+1}{\sqrt{x}+2}=3+\dfrac{1}{\sqrt{x}+2}\)
D lớn nhất \(\Leftrightarrow\sqrt{x}+2\) nhỏ nhất:
Mà:\(\sqrt{x}+2\ge2\)
vậy:\(\max\limits_D=3+\dfrac{1}{2}=\dfrac{7}{2}\Leftrightarrow x=0\)
D=3(căn x +2)/căn x +2 + 1/căn x +2
=3 + 1/ căn x +2 >=3
D lớn nhất khi 1/căn x + 2 lớn nhất
khi căn x + 2 >=2
khi căn x =0
suy ra x=0
Giải chi tiết giúp mình bài này hộ với ạ
(√27 - 3√2 +2√6) : 3√3
đề như thế này à \(\dfrac{\sqrt{27-3\sqrt{2}+2\sqrt{6}}}{3\sqrt{3}}\)
và bài này luôn quên không viết
√(√3 +1)^2 + √(1- √3)^2
\(\sqrt{\left(\sqrt{3}+1\right)^2}+\sqrt{\left(1-\sqrt{3}\right)^2}=\sqrt{3}+1\sqrt{3}-1=2\sqrt{3}\)
Giải chi tiết hộ em với ạ em đang cần gấp ạ

Giải chi tiết hộ em với ạ

 Giải chi tiết hộ em với ạ
Giải chi tiết hộ em với ạ
ĐKXĐ: \(-1\le x\le4\)
\(\Leftrightarrow\left(x-3\right)\sqrt{1+x}-\left(x-3\right)+x-x\sqrt{4-x}=2x^2-6x\)
\(\Leftrightarrow\left(x-3\right)\left(\sqrt{1+x}-1\right)+x\left(1-\sqrt{4-x}\right)=2x^2-6x\)
\(\Leftrightarrow\dfrac{x\left(x-3\right)}{\sqrt{1+x}+1}+\dfrac{x\left(x-3\right)}{1+\sqrt{4-x}}=2\left(x^2-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x=0\Rightarrow x=...\\\dfrac{1}{\sqrt{1+x}+1}+\dfrac{1}{1+\sqrt{4-x}}=2\left(1\right)\end{matrix}\right.\)
Xét (1), do \(VT< \dfrac{1}{1}+\dfrac{1}{1}=2\Rightarrow VT< VP\Rightarrow\left(1\right)\) vô nghiệm
Vậy ...