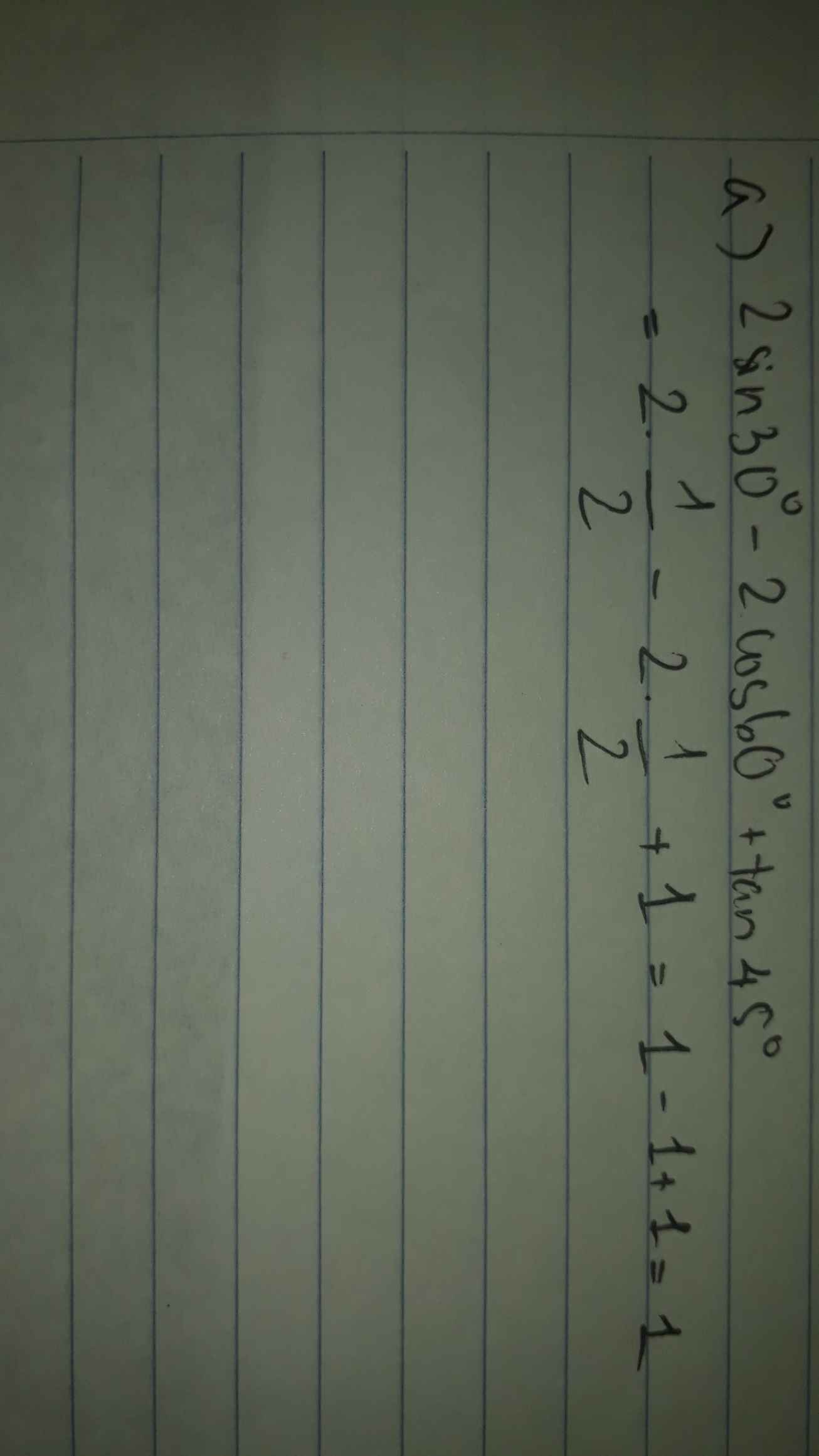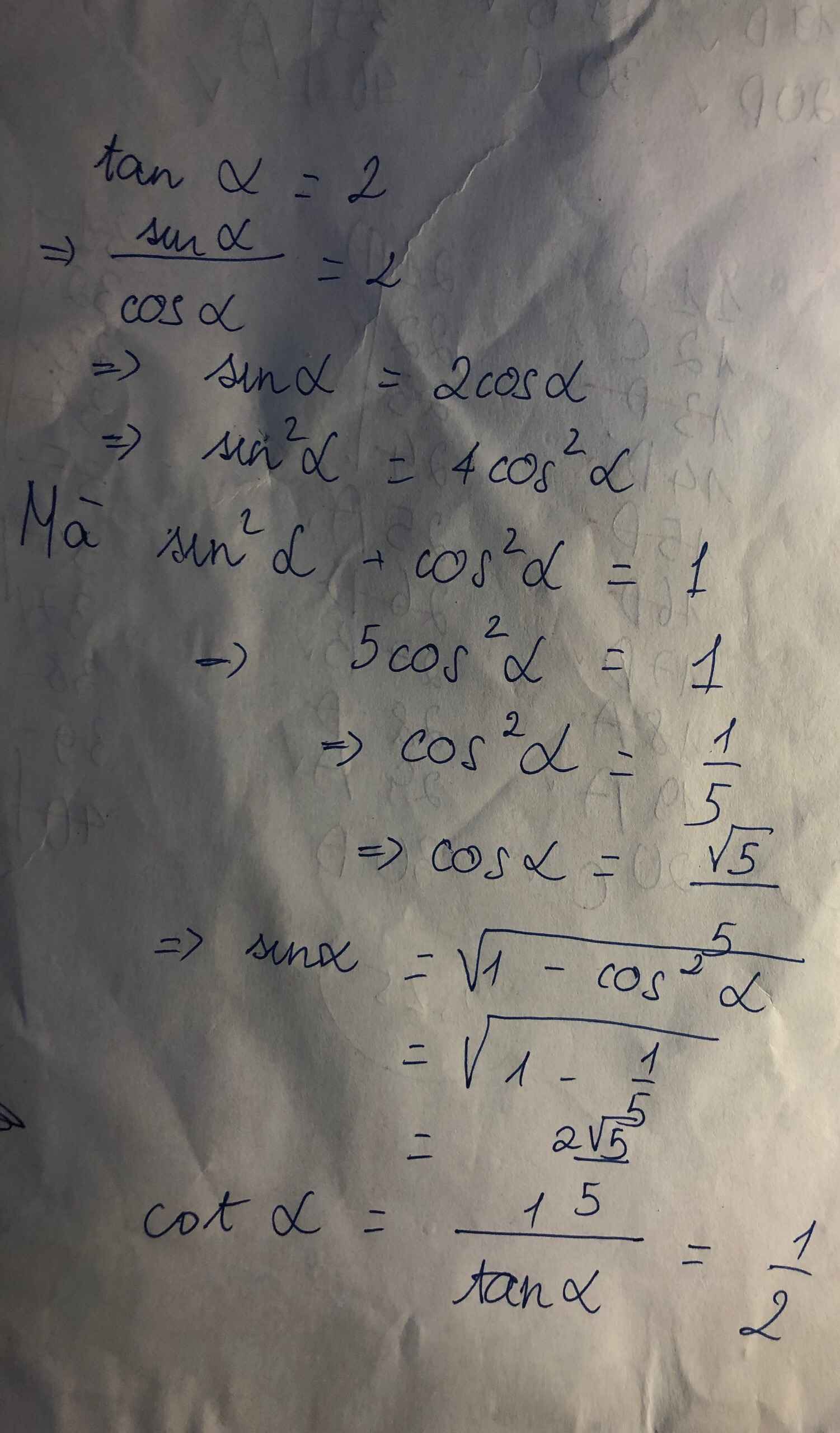A= cos2 10° + cos2 20° + cos2 70° + cos2 80° ( giải chi tiết giúp mình với )

Những câu hỏi liên quan
Bài 4. a) Tính giá trị biểu thức:
A = cos2 20° + cos2 40° + cos2 50° + cos2 70°.
b) Rút gọn biểu thức:
B = sin6 a + cos6 a + 3 sin2 a. cos2 a
\(a,A=\left(\cos^220^0+\cos^270^0\right)+\left(\cos^240^0+\cos^250^0\right)\\ A=\left(\cos^220^0+\sin^220^0\right)+\left(\cos^240^0+\sin^240^0\right)=1+1=2\\ b,B=\left(\cos^2\alpha\right)^3+\left(\sin^2\alpha\right)^3+3\sin^2\alpha\cdot\cos^2\alpha\cdot\left(\sin^2\alpha+\cos^2\alpha\right)\\ B=\left(\sin^2\alpha+\cos^2\alpha\right)^3=1^3=1\)
Đúng 0
Bình luận (0)
Bài 3: Tính:
a. 2sin30o - 2cos60o + tan45o
b. cos2 20o + cos2 40o + cos2 50o + cos2 70o
a, \(2sin30^o-2cos60^o+tan45^o\)
\(=2cos60^o-2cos60^o+tan45^o\)
\(=tan45^o\)
\(=1\)
Đúng 0
Bình luận (0)
b, \(cos^220^o+cos^240^o+cos^250^o+cos^270^o\)
\(=cos^220^o+cos^240^o+sin^240^o+sin^220^o\)
\(=cos^220^o+sin^220^o+cos^240^o+sin^240^o\)
\(=1+1=2\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Biết sinα = \(\dfrac{\sqrt{3}}{2}\). Hãy tính cosα, tanα, cotα.
Bài 2: Biết tanα = 2. Hãy tính sinα, cotα, cosα
Bài 3: Tính: A= cos2 20o + cos2 40o + cos2 50o + cos2 70o
Bài 3:
Ta có: \(A=\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)
\(=\left(\sin^270^0+\cos^270^0\right)+\left(\sin^250^0+\cos^250^0\right)\)
=1+1
=2
Đúng 0
Bình luận (0)
Chứng minh: cos2 (a - b) - cos2 (a + b) = sin2a.sin2b
cos^2(a-b)-cos^2(a+b)
=[cos(a-b)-cos(a+b)]*[cos(a-b)+cos(a+b)]
=[cosa*cosb+sina*sinb-cosa*cosb+sina*sinb]*[cosa*cosb+sina*sinb+cosa*cosb-sina*sinb]
=2*sina*sin*b*2*cosa*cosb
=sin2a*sin2b
Đúng 1
Bình luận (0)
Biểu thức A = cos2x + cos2(\(\dfrac{\pi}{3}\)+x) +cos2(\(\dfrac{\pi}{3}\)-x) không phụ thuộc vào x và bằng :
\(A=cos^2x+\dfrac{1+cos\left(\dfrac{2\pi}{3}+2x\right)}{2}+\dfrac{1+cos\left(\dfrac{2\pi}{3}-2x\right)}{2}\\ =cos^2x+1+\dfrac{cos\left(\dfrac{2\pi}{3}+2x\right)+cos\left(\dfrac{2\pi}{3}-2x\right)}{2}\\ =cos^2x+1+cos\left(\dfrac{2\pi}{3}\right).cos2x\\ =cos^2x+1-\dfrac{1}{2}.cos2x=\dfrac{1+cos2x}{2}+1-\dfrac{cos2x}{2}=\dfrac{3}{2}.\)
Đúng 1
Bình luận (0)
rút gọn biểu thức
a. 1 - sin2 2
b. (1+cos2) (1 - cos2)
c. sin4 2 + cos4 2 + 2sin2 2 cos2 2
giúp mình với
Chứng minh đẳng thức
a) \(\dfrac{1-sin2\alpha+cos2\alpha}{1+sin2\alpha+cos2\alpha}=tan\left(\dfrac{\pi}{4}-\alpha\right)\)
b) \(\dfrac{1-cos\alpha+cos2\alpha}{sin2\alpha-sin\alpha}=cot\alpha\)
\(\dfrac{1+cos2a-sin2a}{1+cos2a+sin2a}=\dfrac{2cos^2a-2sina.cosa}{2cos^2a+2sinacosa}\)
\(=\dfrac{2cosa\left(cosa-sina\right)}{2cosa\left(cosa+sina\right)}=\dfrac{cosa-sina}{cosa+sina}=\dfrac{\sqrt{2}sin\left(\dfrac{\pi}{4}-a\right)}{\sqrt{2}cos\left(\dfrac{\pi}{4}-a\right)}=tan\left(\dfrac{\pi}{4}-a\right)\)
\(\dfrac{1+cos2a-cosa}{sin2a-sina}=\dfrac{2cos^2a-cosa}{2sina.cosa-sina}=\dfrac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\dfrac{cosa}{sina}=cota\)
Đúng 0
Bình luận (0)
a) Biết sin2=\(\dfrac{9}{15}tính\cos2,\tan2,\cot,biết\cos2=\dfrac{3}{5}tính\sin2,\tan2,\cot2\)
1. cos 2a + cos 2b - 2 cos(a+b) cos( a-b)
2. cos2a + sin2b 1
3. cos a2 + sin b2 1
4. cos2 a + sin2 a 1
5. cos 2a cos2 a - 2 sin 2a
6. sin 2a - 2 sin a. cos a.
7. sin 2a cos2 a - sin2 a
8. sin 2a - sin 2b 2 sin ( a+b) cos ( a - b)
9. sin 2a - sin 2b 2 cos( a+b) sin ( a - b)
10. cos a2 + sin a2 1
Câu số mấy đúng?
Đọc tiếp
1. cos 2a + cos 2b = - 2 cos(a+b) cos( a-b)
2. cos2a + sin2b = 1
3. cos a2 + sin b2= 1
4. cos2 a + sin2 a = 1
5. cos 2a = cos2 a - 2 sin 2a
6. sin 2a = - 2 sin a. cos a.
7. sin 2a = cos2 a - sin2 a
8. sin 2a - sin 2b= 2 sin ( a+b) cos ( a - b)
9. sin 2a - sin 2b= 2 cos( a+b) sin ( a - b)
10. cos a2 + sin a2 = 1
Câu số mấy đúng?