cos^2(a-b)-cos^2(a+b)
=[cos(a-b)-cos(a+b)]*[cos(a-b)+cos(a+b)]
=[cosa*cosb+sina*sinb-cosa*cosb+sina*sinb]*[cosa*cosb+sina*sinb+cosa*cosb-sina*sinb]
=2*sina*sin*b*2*cosa*cosb
=sin2a*sin2b
cos^2(a-b)-cos^2(a+b)
=[cos(a-b)-cos(a+b)]*[cos(a-b)+cos(a+b)]
=[cosa*cosb+sina*sinb-cosa*cosb+sina*sinb]*[cosa*cosb+sina*sinb+cosa*cosb-sina*sinb]
=2*sina*sin*b*2*cosa*cosb
=sin2a*sin2b
Chứng minh: cos2 (a - b) - sin2 (a + b) = cos2a.cos2b
Chứng minh
sin2(45độ+@) - sin2(30độ - @) - sin 15 độ . cos2( 15 độ + 2@ ) = sin 2@
Dấu alpha minh ko gỏ đc nên thế bằng @ nha.
CM: (Sina - Cosa)2 =\(\sqrt{2}\) Cos2(a+\(\dfrac{\pi}{4}\))
Chứng minh rằng cos2(x + kπ) = cos2x, k ∈ Z. Từ đó vẽ đồ thị hàm số y = cos2x
Từ đồ thị hàm số y = cos2x, hãy vẽ đồ thị hàm số y = |cos2x|
giải các phương trình sau : a). sin 2x+sin2 x=1/2
b.2sin2 x +3 sin x cosx + cos2 x= 0
c.sin2 x/2 + sin x - 2 cos 2 x/2 = 1/2
Giải phương trình: cos2( π 3 + x) + 4cos( π 6 – x) = 4
A. x = ± π 6 + k2π, k ∈ Z
B. x = ± 5 π 6 + k2π, k ∈ Z
C. x = π 6 + k2π, k ∈ Z
D. Đáp án khác
Xét dãy số \(\left\{x_n\right\}^{+\infty}_{n=1}\) như sau: \(x_1=1\) và với mọi \(n=1,2,...\) thì
\(x_{n+1}=\dfrac{\left(2+\cos\alpha\right)x_n+\cos^2\alpha}{\left(2-2\cos2\alpha\right)x_n+2-2\cos2\alpha}\),
trong đó \(\alpha\) là một tham số thực. Tìm tất cả các giá trị của \(\alpha\) để dãy số \(\left\{y_n\right\}\), với \(y_n=\sum\limits^n_{k=1}\dfrac{1}{2x_k+1},\forall n=1,2,...\) có giới hạn hữu hạn khi \(n\rightarrow+\infty\). Hãy tìm giới hạn của dãy số \(\left\{y_n\right\}\) trong các trường hợp đó.
Xét hàm số y = f x = 1 + cos 2 2 x . Chọn câu đúng:
A. ![]()
B. 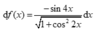
C. ![]()
D. ![]()
Phương trình 2 cos 2 x + cos x - 3 = 0 có nghiệm là:
![]()
![]()
![]()
![]()