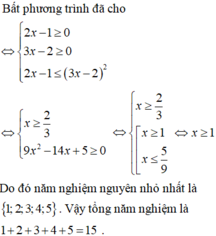bpt \(\sqrt{2x-1}\le3x-2\)có tổng 5 nghiệm nguyên nhỏ nhất là

Những câu hỏi liên quan
Bpt \(\sqrt{2x-1}\le3x-2\)có tổng 5 nghiệm nguyên nhỏ nhất là ?
1+5+10-6=10 trung tony tv co ai la phan cua anh tony tv khong?
bpt \(\sqrt{2x-1}\le3x-2\) có tổng 5 nghiệm nguyên nhỏ nhất là
ĐKXĐ: \(x\ge\frac{1}{2}\)
- Với \(x< \frac{2}{3}\Rightarrow\left\{{}\begin{matrix}VT\ge0\\VP< 0\end{matrix}\right.\) BPT vô nghiệm
- Với \(x\ge\frac{2}{3}\) hai vế ko âm, bình phương ta được:
\(2x-1\le9x^2-12x+4\)
\(\Leftrightarrow9x^2-14x+5\ge0\) \(\Rightarrow x\ge1\)
Vậy tổng 5 nghiệm nguyên nhỏ nhất là 15
1. Biết rằng tập nghiệm của bpt \(\sqrt{2x-4}-2\sqrt{2-x}\ge\dfrac{6x-4}{5\sqrt{x^2+1}}\) là \(\left[a;b\right]\) . Tính P=3a-2b
2. Tính tổng các giá trị nguyên dương của m để tập nghiệm của bpt \(\sqrt{\dfrac{m}{72}x^2+1}< \sqrt{x}\) có chứa đúng 2 số nguyên
1.
ĐKXĐ: \(x=2\)
Xét \(x=2\), bất phương trình vô nghiệm
\(\Rightarrow\) bất phương trình đã cho vô nghiệm
\(\Rightarrow\) Không tồn tại \(a,b\) thỏa mãn
Đề bài lỗi chăng.
Đúng 0
Bình luận (0)
Câu 1: Gọi a,v lần lượt là các nghiệm nguyên nhỏ nhất và lớn nhất của bpt √2x²-5x+2 0 với mọi số thực x
Xem chi tiết
Bất phương trình 2 x - 1 ≤ 3 x - 2 có tổng năm nghiệm nguyên nhỏ nhất là
A. 10.
B. 20.
C. 15.
D. 5
Bất phương trình
2
x
-
1
≤
3
x
-
2
có tổng năm nghiệm nguyên nhỏ nhất là A. 15. B. 20. C. 10. D. 5.
Đọc tiếp
Bất phương trình 2 x - 1 ≤ 3 x - 2 có tổng năm nghiệm nguyên nhỏ nhất là
A. 15.
B. 20.
C. 10.
D. 5.
tìm tập nghiệm của bpt: \(\sqrt{2x+3}-\sqrt{x+1}>3x+2\sqrt{2x^2+5x-3}-16\) có nghiệm
Câu 1: Tìm giá trị của m để phương trình mx²-2(m 2) 2 3m=0 vô nghiệm Câu 2:Cho bpt x² -5x 4-2√x-1. Nghiệm nguyên nhỏ nhất của bpt.
Xem chi tiết
Câu 1:
Ta có: \(\Delta=\left[-2\left(m+2\right)\right]^2-4\cdot m\cdot\left(2+3m\right)\)
\(\Leftrightarrow\Delta=\left(2m+4\right)^2-4m\left(2+3m\right)\)
\(\Leftrightarrow\Delta=4m^2+16m+16-8m-12m^2\)
\(\Leftrightarrow\Delta=-8m^2+8m+16\)
\(\Leftrightarrow\Delta=-8\left(m^2-m-2\right)\)
Để phương trình vô nghiệm thì \(\Delta< 0\)
\(\Leftrightarrow m^2-m-2>0\)
\(\Leftrightarrow\left(m-2\right)\left(m+1\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m-2>0\\m+1>0\end{matrix}\right.\\\left\{{}\begin{matrix}m-2< 0\\m+1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m>2\\m>-1\end{matrix}\right.\\\left\{{}\begin{matrix}m< 2\\m< -1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Câu 1
Để pt vô nghiệm \(\Rightarrow\Delta'=\left(m+2\right)^2-\left(3m+2\right)m=m^2+4m+4-3m^2-2m=-2m^2+2m+4=-2\left(m^2-m-2\right)=-2\left(m+1\right)\left(m-2\right)< 0\) \(\Leftrightarrow\left(m+1\right)\left(m-2\right)>0\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho bpt \(\sqrt{x^2-3x+m}>2x+1\) tìm m để bpt có nghiệm x ∈\(\left[0;2\right]\)
Khi \(x\ge0\Rightarrow2x+1>0\) nên BPT tương đương:
\(x^2-3x+m>\left(2x+1\right)^2\)
\(\Leftrightarrow x^2-3x+m>4x^2+4x+1\)
\(\Leftrightarrow3x^2+7x+1< m\)
Xét hàm \(f\left(x\right)=3x^2+7x+1\) trên \(\left[0;2\right]\)
\(-\dfrac{b}{2a}=-\dfrac{7}{6}\notin\left[0;2\right]\) ; \(f\left(0\right)=1\) ; \(f\left(2\right)=27\)
\(\Rightarrow f\left(x\right)\ge1\Rightarrow\) pt có nghiệm trên đoạn đã cho khi \(m>1\)
Đúng 1
Bình luận (0)