Cho các số thực m,n,p thỏa mãn :n2+np+p2=1-(3m2/2)
Tìm min,max của A=m+n+p
Cho m,n là các số thực không âm thỏa mãn \(m^2+n^2=4\).Tìm Min,Max:
\(P=\sqrt{3-m^2}+\sqrt{3-n^2}\)
\(P\ge\sqrt{3-m^2+3-n^2}=\sqrt{2}\)
\(P_{min}=\sqrt{2}\) khi \(\left[{}\begin{matrix}\sqrt{3-m^2}=0\\\sqrt{3-n^2}=0\end{matrix}\right.\) \(\Leftrightarrow\left(m;n\right)=\left(1;\sqrt{3}\right);\left(\sqrt{3};1\right)\)
\(P\le\sqrt{2\left(3-m^2+3-n^2\right)}=2\)
\(P_{max}=2\) khi \(m=n=\sqrt{2}\)
1) cho các số thực dương a,b thỏa mãn \(3a+b\le1\). Tìm Min của \(P=\dfrac{1}{a}+\dfrac{1}{\sqrt{ab}}\)
2) Với hai số thực a,b không âm thỏa mãn \(a^2+b^2=4\). Tìm Max \(M=\dfrac{ab}{a+b+2}\)
3) Cho x,y khác 0 thỏa mãn \(\left(x+y\right)xy=x^2+y^2-xy\). Tìm Max \(A=\dfrac{1}{x^3}+\dfrac{1}{y^3}\)
1) Áp dụng bất đẳng thức AM - GM và bất đẳng thức Schwarz:
\(P=\dfrac{1}{a}+\dfrac{1}{\sqrt{ab}}\ge\dfrac{1}{a}+\dfrac{1}{\dfrac{a+b}{2}}\ge\dfrac{4}{a+\dfrac{a+b}{2}}=\dfrac{8}{3a+b}\ge8\).
Đẳng thức xảy ra khi a = b = \(\dfrac{1}{4}\).
2.
\(4=a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\Rightarrow a+b\le2\sqrt{2}\)
Đồng thời \(\left(a+b\right)^2\ge a^2+b^2\Rightarrow a+b\ge2\)
\(M\le\dfrac{\left(a+b\right)^2}{4\left(a+b+2\right)}=\dfrac{x^2}{4\left(x+2\right)}\) (với \(x=a+b\Rightarrow2\le x\le2\sqrt{2}\) )
\(M\le\dfrac{x^2}{4\left(x+2\right)}-\sqrt{2}+1+\sqrt{2}-1\)
\(M\le\dfrac{\left(2\sqrt{2}-x\right)\left(x+4-2\sqrt{2}\right)}{4\left(x+2\right)}+\sqrt{2}-1\le\sqrt{2}-1\)
Dấu "=" xảy ra khi \(x=2\sqrt{2}\) hay \(a=b=\sqrt{2}\)
3. Chia 2 vế giả thiết cho \(x^2y^2\)
\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\ge\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\)
\(\Rightarrow0\le\dfrac{1}{x}+\dfrac{1}{y}\le4\)
\(A=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\right)=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\le16\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
Bài 1: CHo 2 số thực x,y sao cho x+y=1. Tìm Min của M=5x2+y2
Bài 2: Cho 2 số x,y thỏa mãn x2+2xy+8(x+y)+2y2+12=0 Tìm Max và Min của N=x+y+1
Cho các số thực a, b, m, n sao cho 2 m + n < 0 và thỏa mãn điều kiện log 2 a 2 + b 2 + 9 = 1 + log 2 3 a + 2 b 9 − m .3 − n .3 − 4 2 m + n + ln 2 m + n + 2 2 + 1 = 81
Tìm giá trị nhỏ nhất của biểu thức P = a − m 2 + b − n 2
A. 2 5 − 2.
B. 2.
C. 5 − 2.
D. 2 5 .
cho số thực a;b;c thỏa mãn \(a^2+b^2+c^2=1\)
tìm min max của \(P=ab+bc+ca\)
Chuyên gia sao lại đi hỏi ( nghĩ chuyên gia phải cái gì cũng biết mà ??? )
Ta có: \(\left(a+b+c\right)^2\ge0\)
<=>\(a^2+b^2+c^2+2\left(ab+bc+ca\right)\ge0\)
<=>\(1+2\left(ab+bc+ca\right)\ge0\)
<=>\(ab+bc+ca\ge\dfrac{-1}{2}\)
hay P\(\ge\dfrac{-1}{2}\)
cho các số thực x,y,z thỏa mãn 2x+3y-z=4. Tìm min max của A =xy+yz+zx
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
![]()
![]()
![]()
![]()
Chọn A.
Ta có ![]()
Giải bất phương trình trên với ẩn |z| ta được:
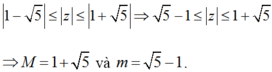
Vậy ![]()
Cho số thực x;y thỏa mãn: x^2 + xy + 2y^2 = 1 Tìm min và max của A = x - 2y + 3
pro rồi thì bạn cần gì mình giải nhỉ
??
\(A=x-2y+3\Rightarrow x=A+2y-3\)
\(\Rightarrow\left(2y+A-3\right)^2+y\left(A+2y-3\right)+2y^2=1\)
\(\Leftrightarrow8y^2+\left(5A-15\right)y+A^2-6A+8=0\)
\(\Delta=\left(5A-15\right)^2-32\left(A^2-6A+8\right)\ge0\)
\(\Leftrightarrow-7A^2+42A-31\ge0\)
\(\Rightarrow\dfrac{21-4\sqrt{14}}{7}\le A\le\dfrac{21+4\sqrt{14}}{7}\)
cho biểu thức \(P=a^4+b^4-ab\), với a,b là các số thực thỏa mãn \(a^2+b^2+ab=3\)
tìm Min và MAx của biểu thức P
Ngắn gọn thì đây là 1 bài toán không giải được (min max tồn tại, nhưng không thể tìm được)
Cực trị xảy ra tại \(x=\dfrac{a}{b}\) là nghiệm của pt bậc 4:
\(7x^4+11x^3-3x^2-4x-2=0\)
Là một pt không thể phân tích về các pt bậc thấp hơn
Nếu sửa đề thế này thì có thể quy về 1 biến khá đơn giản:
\(3-ab=a^2+b^2\ge2ab\Rightarrow ab\le1\)
\(3-ab=a^2+b^2\ge-2ab\Rightarrow ab\ge-3\)
\(\Rightarrow-3\le ab\le1\)
\(P=\left(a^2+b^2\right)^2-2a^2b^2-ab=\left(3-ab\right)^2-2a^2b^2-ab=-a^2b^2-7ab+9\)
Đặt \(ab=x\Rightarrow-3\le x\le1\)
\(P=-x^2-7x+9=\left(-x^2-7x+8\right)+1=1+\left(1-x\right)\left(x+8\right)\ge1\)
\(P=\left(-x^2-7x-12\right)+21=21-\left(x+3\right)\left(x+4\right)\le21\)