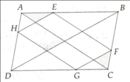
Cho điểm M nằm trong hình bình hành ABCD sao cho\MAB = MCB [.
Qua M vẽ đường thẳng song song với BC, cắt AB và CD theo thứ tự ở G và H.
Qua M vẽ đường thẳng song song với AB, cắt BC ở F. Chứng minh rằng:
1. Tam giác AGM đồng dạng với tam giác CFM.
2. góc MBC =góc MDC

Những câu hỏi liên quan
Cho điểm M nằm trong hình bình hành ABCD sao cho\MAB = MCB [.
Qua M vẽ đường thẳng song song với BC, cắt AB và CD theo thứ tự ở G và H.
Qua M vẽ đường thẳng song song với AB, cắt BC ở F. Chứng minh rằng:
1. Tam giác AGM đồng dạng với tam giác CFM.
2. góc MBC =góc MDC
Please giúp mình chỉ rõ cả 2 ý
Cho điểm M nằm trong hbh ABCD sao cho góc MAB = góc MCB. Qua M vẽ đường thẳng song song với BC cắt AB, CD theo thứ tự ở G,H. Qua M vẽ đường thẳng song song với AB cắt BC ở F. CMR:
a) Tam giác AGM đồng dạng với Tam giác CFM
b) Góc MBC = Góc MDC
Help me!!!
vì AB // DC , AD //GH
=> AGHD là hbh =>AG=DH
TT TA ĐƯỢC FC=MH ;MG=BF
VÍ ΔAGM ∼ ΔCFM theo a
=>\(\dfrac{AG}{CF}=\dfrac{MG}{MF}\)
MÀ AG=DH; FC=MH ;MG=BF
=>\(\dfrac{DH}{MH}=\dfrac{BF}{MF}\) (1)
MF//HC=> GÓC MFB=GÓC DCF
TA LẠI CÓ GH //BC=> GÓC DCF= GÓC DHM (2)
TỪ (1) VÀ (2)
=> ΔDHM ∼ Δ BFM (c-g-c)
=> góc MDC =góc MBF
từ đó => góc MDC =góc MBC (đpcm)
Đúng 1
Bình luận (1)
@Phùng Khánh Linh, Nhã Doanh, Mashiro Shiina, Akai Haruma, Hoàng Anh Thư, ngonhuminh, Nguyễn Thanh Hằng, Cold Wind, Đời về cơ bản là buồn... cười!!!, Phạm Nguyễn Tất Đạt, kuroba kaito, nguyen thi vang, Mến Vũ, Nguyễn Huy Tú, ...
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 6: Cho hình thang ABCD có hai đáy là AB và CD. Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự ở E và F. a) Chứng minh ED/AD + BF/BC 1b) Các đường chéo của hình thang cắt nhau tại O. Chứng minh OA.OD OB.OC.Bài 7: Cho tam giác ABC nhọn, M là trung điểm của BC, E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC cắt AB ở D, cắt AM ở K. Qua E kẻ đường thẳng song song với AB cắt AC ở F.a) Chứng minh CF DKb) Gọi H là trực tâm của tam giác ABC. Đường thẳng qua H vu...
Đọc tiếp
Bài 6: Cho hình thang ABCD có hai đáy là AB và CD. Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự ở E và F.
a) Chứng minh ED/AD + BF/BC = 1
b) Các đường chéo của hình thang cắt nhau tại O. Chứng minh OA.OD = OB.OC.
Bài 7: Cho tam giác ABC nhọn, M là trung điểm của BC, E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC cắt AB ở D, cắt AM ở K. Qua E kẻ đường thẳng song song với AB cắt AC ở F.
a) Chứng minh CF = DK
b) Gọi H là trực tâm của tam giác ABC. Đường thẳng qua H vuông góc với MH cắt AB và AC theo thứ tự ở I và K’. Qua C kẻ đường thẳng song song với IK’, cắt AH và AB theo thứ tự ở N và P. Chứng minh NC = NP và HI = HK’.
Bài 8: Cho tam giác ABC, điểm M bất kì trên cạnh AB. Qua M kẻ đường thẳng song song với BC cắt AC ở N biết AM = 11 cm, MB = 8 cm, AC = 38 cm. Tính độ dài các đoạn thẳng AN, NC.
Bài 9: Cho góc xAy, trên tia Ax lấy hai điểm D và E, trên tia Ay lấy hai điểm F và G sao cho FD song song với EG. Đường thẳng qua G song song với FE cắt tia Ax tại H. Chứng minh AE 2 = AD.AH.
Bài 10: Cho hình bình hành ABCD. Gọi E là một điểm bất kì trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ quá F song song với BD cắt CD ở G. Chứng minh AH.CD = AD.CG.
Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )
chắc sang năm mới làm xong mất
sang năm mk giúp bn na
Xem thêm câu trả lời
Cho hình bình hành ABCD. Gọi E là một điểm bất kỳ trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ qua F song song với BD cắt CD ở G. Chứng minh A H . C D = A D . C G .
Cho tứ giác ABCD có AB song song với CD. Các đường thẳng AC, BD cắt nhau ở E và các đường thẳng AD, BC cắt nhau ở F. Gọi M, N theo thứ tự là trung điểm cạnh AB, CD. Chứng minh rằng E, F, M, N cùng nằm trên một đường thẳng.
Đặt \(\frac{AB}{CD}=k\)
Do AB // CD nên \(\frac{EA}{EC}=\frac{EB}{ED}=k\) và \(\frac{FA}{FD}=\frac{FB}{FC}=k\) (như hình vẽ)
Suy ra : \(\overrightarrow{EA}=-k\overrightarrow{EC}\), \(\overrightarrow{EB}=-k\overrightarrow{ED}\) , \(\overrightarrow{FA}=-k\overrightarrow{FD}\) và \(\overrightarrow{FB}=-k\overrightarrow{FC}\)
Do M là trung điểm AB và N là trung điểm CD nên :
\(2\overrightarrow{EM}=\overrightarrow{EA}+\overrightarrow{EB}=-k\overrightarrow{EC}-k\overrightarrow{ED}=-2\left(\overrightarrow{EC}+\overrightarrow{ED}\right)=-2k\overrightarrow{EN}\)
Suy ra \(\overrightarrow{EM}=k\overrightarrow{EN}\) (1)
Hoàn toàn tương tự cũng được \(\overrightarrow{FM}=k\overrightarrow{FN}\) (2)
Từ (1) và (2) suy ra điều cần chứng minh
Đúng 0
Bình luận (0)
BÀI 1: Cho tam giác ABC có D, E, F theo thứ tự là trung điểm của AB, AC, BC. Chứng minh BDEF là hình bình hành và suy ra BÀI 2: Cho hình bình hành ABCD (AB CD). Tia phân giác của góc A cắt BC tại I, tia phân giác góc C cắt AD tại K. Chứng minh: AICK là hình bình hành.BÀI 3: Cho tam giác ABC. Đường thẳng qua B song song với AC cắt đường thẳng qua C song song với AB ở D.a) Chứng minh rằng tư giác ABDC là hình bình hành.b) Gọi M là trung điểm cạnh BC. Chứng minh rằng ba điểm A, M, D thẳng hàng.
Đọc tiếp
BÀI 1: Cho tam giác ABC có D, E, F theo thứ tự là trung điểm của AB, AC, BC. Chứng minh BDEF là hình bình hành và suy ra
BÀI 2: Cho hình bình hành ABCD (AB < CD). Tia phân giác của góc A cắt BC tại I, tia phân giác góc C cắt AD tại K. Chứng minh: AICK là hình bình hành.
BÀI 3: Cho tam giác ABC. Đường thẳng qua B song song với AC cắt đường thẳng qua C song song với AB ở D.
a) Chứng minh rằng tư giác ABDC là hình bình hành.
b) Gọi M là trung điểm cạnh BC. Chứng minh rằng ba điểm A, M, D thẳng hàng.
Cho hình bình hành ABCD. Gọi E là một điểm bất kì trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ quá F song song với BD cắt CD ở G. Chứng minh AH.CD = AD.CG.

Áp dụng định lý Thalès, ta có:
HE // BD \(\Rightarrow\frac{AH}{AD}=\frac{AE}{AB}\)(1)
EF // AC \(\Rightarrow\frac{AE}{AB}=\frac{FC}{BC}\)(2)
FG // BD \(\Rightarrow\frac{FC}{BC}=\frac{GC}{DC}\)(3)
Từ (1),(2),(3) suy ra \(\frac{AH}{AD}=\frac{GC}{DC}\Rightarrow AH.CD=AD.CG\left(đpcm\right)\)
cho hình thang ABCD ( AB// CD , AB<CD ) AC cắt BD tại I . Từ I vẽ đường thẳng song song với AB cắt AD và BC theo thứ tự ở M ,N . Chứng minh IM =IN
cho hình thang ABCD ( AB// CD , AB<CD ) AC cắt BD tại I . Từ I vẽ đường thẳng song song với AB cắt AD và BC theo thứ tự ở M ,N . Chứng minh IM =IN