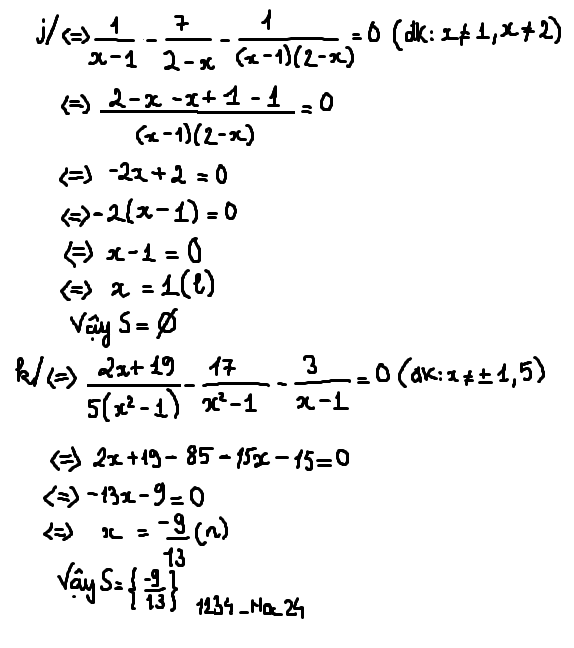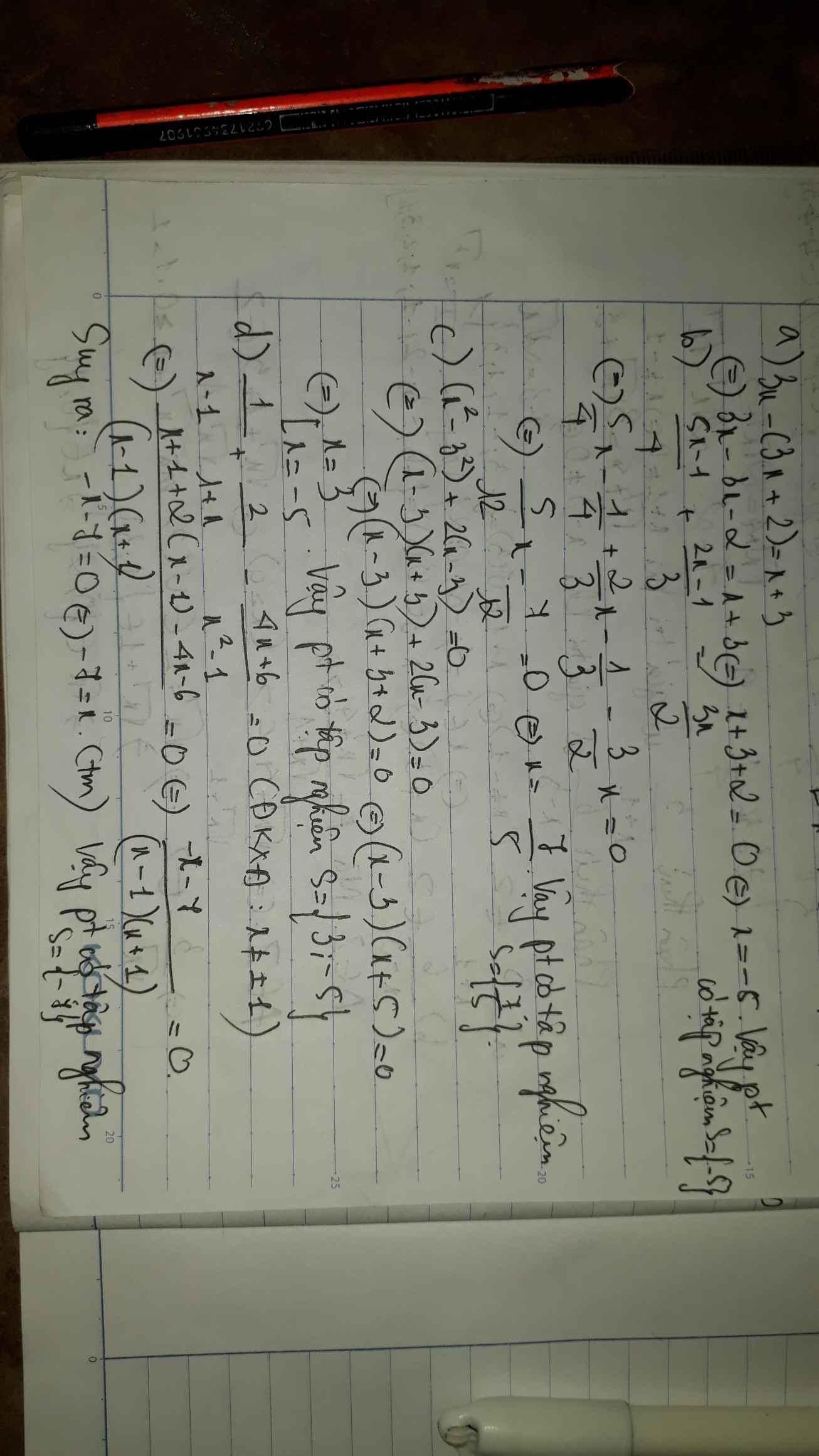\(\frac{x+3}{57}+\frac{x+4}{28}+\frac{x+117}{19}=0\)

⇔\(\left(\frac{x+3}{57}+1\right)+\left(\frac{x+4}{28}+2\right)+\left(\frac{x+117}{19}-3\right)\)= \(0\)

⇔ \(\frac{x+60}{57}+\frac{x+60}{28}+\frac{x+60}{19}=0\)

⇔\(\left(x+60\right)\left(\frac{1}{57}+\frac{1}{28}+\frac{1}{19}\right)=0\)

⇔\(x+60=0\left(do\frac{1}{57}+\frac{1}{28}+\frac{1}{19}>0\right)\)

⇔\(x=-60\)

Vậy S={-60}

ĐKXĐ: \(x\neq 0\).

Đặt \(\dfrac{x}{3}-\dfrac{4}{x}=t\).

PT đã cho tương đương:

\(3t^2+8-10t=0\)

\(\Leftrightarrow\left(t-2\right)\left(3t-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t=2\\t=\dfrac{4}{3}\end{matrix}\right.\).

Với t = 2 ta có \(\dfrac{x}{3}-\dfrac{4}{x}=2\Leftrightarrow\dfrac{x^2-12}{3x}=2\Leftrightarrow x^2-6x-12=0\Leftrightarrow x=\pm\sqrt{21}+3\).

Với t = \(\frac{4}{3}\) ta có \(\dfrac{x}{3}-\dfrac{4}{x}=\dfrac{4}{3}\Leftrightarrow\dfrac{x^2-12}{3x}=\dfrac{4}{3}\Leftrightarrow x^2-12=4x\Leftrightarrow x^2-4x-12=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\).

Vậy...

d: Ta có: \(\dfrac{x}{x+3}-\dfrac{2x}{x-3}-\dfrac{3x}{9-x^2}=0\)

\(\Leftrightarrow x^2-3x-2x^2-6x+3x=0\)

\(\Leftrightarrow-x^2-6x=0\)

\(\Leftrightarrow-x\left(x+6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-6\left(nhận\right)\end{matrix}\right.\)

a: Ta có: \(3\left(x-1\right)-3=2\left(x+3\right)\)

\(\Leftrightarrow3x-3-3=2x+6\)

\(\Leftrightarrow x=12\)

b: Ta có: \(\dfrac{x+4}{4}-\dfrac{x+3}{3}=\dfrac{x+6}{6}\)

\(\Leftrightarrow3x+12-4x-12=2x+12\)

\(\Leftrightarrow-3x=12\)

hay x=-4

c: Ta có: \(\left(2x-1\right)^2-x^2=0\)

\(\Leftrightarrow\left(x-1\right)\left(3x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\end{matrix}\right.\)

a) Ta có: \(\dfrac{x-3}{5}=6-\dfrac{1-2x}{3}\)

\(\Leftrightarrow\dfrac{3\left(x-3\right)}{15}=\dfrac{90}{15}-\dfrac{5\left(1-2x\right)}{15}\)

\(\Leftrightarrow3x-9=90-5+10x\)

\(\Leftrightarrow3x-9=10x+85\)

\(\Leftrightarrow3x-10x=85+9\)

\(\Leftrightarrow-7x=94\)

hay \(x=-\dfrac{94}{7}\)

Vậy: \(S=\left\{-\dfrac{94}{7}\right\}\)

b) Ta có: \(\dfrac{3x-2}{6}-5=\dfrac{3-2\left(x+7\right)}{4}\)

\(\Leftrightarrow\dfrac{2\left(3x-2\right)}{12}-\dfrac{60}{12}=\dfrac{3\left(3-2x-14\right)}{12}\)

\(\Leftrightarrow6x-4-60=9-6x-42\)

\(\Leftrightarrow6x-64=-6x-33\)

\(\Leftrightarrow6x+6x=-33+64\)

\(\Leftrightarrow12x=31\)

hay \(x=\dfrac{31}{12}\)

Vậy: \(S=\left\{\dfrac{31}{12}\right\}\)

c) Ta có: \(3\left(x-1\right)+3=5x\)

\(\Leftrightarrow3x-3+3=5x\)

\(\Leftrightarrow3x-5x=0\)

\(\Leftrightarrow-2x=0\)

hay x=0

Vậy: S={0}

d) Ta có: \(\dfrac{x+1}{100}+\dfrac{x+2}{99}=\dfrac{x+3}{98}+\dfrac{x+4}{97}\)

\(\Leftrightarrow\dfrac{x+1}{100}+1+\dfrac{x+2}{99}+1=\dfrac{x+3}{98}+1+\dfrac{x+4}{97}+1\)

\(\Leftrightarrow\dfrac{x+101}{100}+\dfrac{x+101}{99}=\dfrac{x+101}{98}+\dfrac{x+101}{97}\)

\(\Leftrightarrow\dfrac{x+101}{100}+\dfrac{x+101}{99}-\dfrac{x+101}{98}-\dfrac{x+101}{97}=0\)

\(\Leftrightarrow\left(x+101\right)\left(\dfrac{1}{100}+\dfrac{1}{99}-\dfrac{1}{98}-\dfrac{1}{97}\right)=0\)

mà \(\dfrac{1}{100}+\dfrac{1}{99}-\dfrac{1}{98}-\dfrac{1}{97}\ne0\)

nên x+101=0

hay x=-101

Vậy: S={-101}

a) \(\dfrac{x-3}{5}=6-\dfrac{1-2x}{3}\\ \Leftrightarrow\dfrac{3\left(x-3\right)}{15}=\dfrac{90-5\left(1-2x\right)}{15}\\ \Leftrightarrow3x-9=90-5+10x\\ \Leftrightarrow3x-10x=90-5+9\\ \Leftrightarrow-7x=94\\ \Leftrightarrow x=\dfrac{-94}{7}\)

Vậy \(x=\dfrac{-94}{7}\) là nghiệm của pt

b) \(\dfrac{3x-2}{6}-5=\dfrac{3-2\left(x+7\right)}{4}\\ \Leftrightarrow\dfrac{2\left(3x-2\right)-60}{12}=\dfrac{9-6\left(x+7\right)}{12}\\ \Leftrightarrow6x-4-60=9-6x-42\\ \Leftrightarrow6x+6x=9-42+4+60\\ \Leftrightarrow12x=31\\ \Leftrightarrow x=\dfrac{31}{12}\)

Vậy \(x=\dfrac{31}{12}\) là nghiệm của pt

c) \(3\left(x-1\right)+3=5x\\ \Leftrightarrow3x+3+3=5x\\ \Leftrightarrow5x-3x=3+3\\ \Leftrightarrow2x=6\\ \Leftrightarrow x=3\)

Vậy x = 3 là nghiệm của pt

d) \(\dfrac{x+1}{100}+\dfrac{x+2}{99}=\dfrac{x+3}{98}+\dfrac{x+4}{97}\\ \Leftrightarrow\left(\dfrac{x+1}{100}+1\right)+\left(\dfrac{x+2}{99}+1\right)=\left(\dfrac{x+3}{98}+1\right)+\left(\dfrac{x+4}{97}+1\right)\\ \Leftrightarrow\dfrac{x+101}{100}+\dfrac{x+101}{99}-\dfrac{x+101}{98}-\dfrac{x+101}{97}=0\\ \Leftrightarrow\left(x+101\right)\left(\dfrac{1}{100}+\dfrac{1}{99}-\dfrac{1}{98}-\dfrac{1}{97}\right)=0\\ \Leftrightarrow x+101=0\\ \Leftrightarrow x=-101\)

Vậy x = -101 là nghiệm của pt

e) \(\dfrac{59-x}{41}+\dfrac{57-x}{43}+\dfrac{55-x}{45}+\dfrac{53-x}{47}=-4\\ \Leftrightarrow\left(\dfrac{59-x}{41}+1\right)+\left(\dfrac{57-x}{43}+1\right)+\left(\dfrac{53-x}{45}+1\right)+\left(\dfrac{53-x}{47}+1\right)=0\\ \Leftrightarrow\dfrac{100-x}{41}+\dfrac{100-x}{43}+\dfrac{100-x}{45}+\dfrac{100-x}{47}=0\\ \Leftrightarrow\left(100-x\right)\left(\dfrac{1}{41}+\dfrac{1}{43}+\dfrac{1}{45}+\dfrac{1}{47}\right)=0\\ \Leftrightarrow100-x=0\\ \Leftrightarrow x=100\)

Vậy x = 100 là nghiệm của pt

f) \(\dfrac{x-90}{10}+\dfrac{x-76}{12}+\dfrac{x-58}{14}+\dfrac{x-36}{16}+\dfrac{x-15}{17}=15\\ \Leftrightarrow\left(\dfrac{x-90}{10}-1\right)+\left(\dfrac{x-76}{12}-2\right)+\left(\dfrac{x-58}{14}-3\right)+\left(\dfrac{x-36}{16}-4\right)+\left(\dfrac{x-15}{17}-5\right)=0\\ \Leftrightarrow\dfrac{x-100}{10}+\dfrac{x-100}{12}+\dfrac{x-100}{14}+\dfrac{x-100}{16}+\dfrac{x-100}{17}=0\\ \Leftrightarrow\left(x-100\right)\left(\dfrac{1}{10}+\dfrac{1}{12}+\dfrac{1}{14}+\dfrac{1}{16}+\dfrac{1}{17}\right)=0\\ \Leftrightarrow x-100=0\\ \Leftrightarrow x=100\)

Vậy x = 100 là nghiệm của pt

e) Ta có: \(\dfrac{59-x}{41}+\dfrac{57-x}{43}+\dfrac{55-x}{45}+\dfrac{53-x}{47}=-4\)

\(\Leftrightarrow\dfrac{59-x}{41}+1+\dfrac{57-x}{43}+1+\dfrac{55-x}{45}+1+\dfrac{53-x}{47}+1=0\)

\(\Leftrightarrow\dfrac{100-x}{41}+\dfrac{100-x}{43}+\dfrac{100-x}{45}+\dfrac{100-x}{47}=0\)

\(\Leftrightarrow\left(100-x\right)\left(\dfrac{1}{41}+\dfrac{1}{43}+\dfrac{1}{45}+\dfrac{1}{47}\right)=0\)

mà \(\dfrac{1}{41}+\dfrac{1}{43}+\dfrac{1}{45}+\dfrac{1}{47}>0\)

nên 100-x=0

hay x=100

Vậy: S={100}

f) Ta có: \(\dfrac{x-90}{10}+\dfrac{x-76}{12}+\dfrac{x-58}{14}+\dfrac{x-36}{16}+\dfrac{x-15}{17}=15\)

\(\Leftrightarrow\dfrac{x-90}{10}-1+\dfrac{x-76}{12}-2+\dfrac{x-58}{14}-3+\dfrac{x-36}{16}-4+\dfrac{x-15}{17}-5=0\)

\(\Leftrightarrow\dfrac{x-100}{10}+\dfrac{x-100}{12}+\dfrac{x-100}{14}+\dfrac{x-100}{16}+\dfrac{x-100}{17}=0\)

\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{10}+\dfrac{1}{12}+\dfrac{1}{14}+\dfrac{1}{16}+\dfrac{1}{17}\right)=0\)

mà \(\dfrac{1}{10}+\dfrac{1}{12}+\dfrac{1}{14}+\dfrac{1}{16}+\dfrac{1}{17}>0\)

nên x-100=0

hay x=100

Vậy: S={100}

Lời giải:
PT $\Leftrightarrow \frac{x-342}{15}-1+\frac{x-323}{17}-2+\frac{x-300}{19}-3+\frac{x-273}{21}-4=0$

$\Leftrightarrow \frac{x-357}{15}+\frac{x-357}{17}+\frac{x-357}{19}+\frac{x-357}{21}=0$

$(x-357)\left(\frac{1}{15}+\frac{1}{17}+\frac{1}{19}+\frac{1}{21}\right)=0$

Dễ thấy: $\frac{1}{15}+\frac{1}{17}+\frac{1}{19}+\frac{1}{21}\neq 0$

$\Rightarrow x-357=0$

$\Rightarrow x=357$

a: Ta có: \(3x-\left(3x+2\right)=x+3\)

\(\Leftrightarrow x+3=-2\)

hay x=-5

b: Ta có: \(\dfrac{5x-1}{4}+\dfrac{2x-1}{3}=\dfrac{3x}{2}\)

\(\Leftrightarrow15x-3+8x-4=18x\)

\(\Leftrightarrow5x=7\)

hay \(x=\dfrac{7}{5}\)

ĐKXĐ : \(x\notin\left\{0;-1;-2;-3;-4\right\}\)

Ta có \(\dfrac{1}{x}+\dfrac{1}{x+1}+\dfrac{1}{x+2}+\dfrac{1}{x+3}+\dfrac{1}{x+4}=0\)

\(\Leftrightarrow\dfrac{2x+4}{x.\left(x+4\right)}+\dfrac{2x+4}{\left(x+1\right).\left(x+3\right)}+\dfrac{1}{x+2}=0\)

\(\Leftrightarrow\dfrac{2x+4}{\left(x+2\right)^2-4}+\dfrac{2x+4}{\left(x+2\right)^2-1}+\dfrac{1}{x+2}=0\) (*)

Đặt x + 2 = a \(\left(a\ne0\right)\) 

(*) \(\Leftrightarrow\dfrac{2a}{a^2-4}+\dfrac{2a}{a^2-1}+\dfrac{1}{a}=0\)

\(\Leftrightarrow\dfrac{2}{a-\dfrac{4}{a}}+\dfrac{2}{a-\dfrac{1}{a}}+\dfrac{1}{a}=0\) (**)

Đặt \(\dfrac{1}{a}=b\left(b\ne0\right)\) \(\Rightarrow ab=1\)

Ta được (**) \(\Leftrightarrow\dfrac{2}{a-4b}+\dfrac{2}{a-b}+b=0\)

\(\Leftrightarrow\dfrac{2b}{1-4b^2}+\dfrac{2b}{1-b^2}+b=0\)

\(\Leftrightarrow\dfrac{2}{1-4b^2}+\dfrac{2}{1-b^2}=-1\)

\(\Rightarrow4-10b^2=-4b^4+5b^2-1\)

\(\Leftrightarrow4b^4-15b^2+5=0\) (***)

Đặt b² = t > 0

Ta có (***) <=> \(4t^2-15t+5=0\Leftrightarrow t=\dfrac{15\pm\sqrt{145}}{8}\) (tm)

\(\Leftrightarrow b=\pm\sqrt{\dfrac{15\pm\sqrt{145}}{8}}\) 

mà x + 2 = a ; ab = 1 

nên \(x=\pm\sqrt{\dfrac{8}{15\pm\sqrt{145}}}-2\)

Thử lại ta có phương trình có 4 nghiệm như trên

\(2x^4+3x^3+8x^2+6x+5=0\)

\(\Leftrightarrow2x^4+2x^3+2x^2+x^3+x^2+x+5x^2+5x+5=0\)

\(\Leftrightarrow2x^2\left(x^2+x+1\right)+x\left(x^2+x+1\right)+5\left(x^2+x+1\right)=0\)

\(\Leftrightarrow\left(x^2+x+1\right)\left(2x^2+x+5\right)=0\)

Mà \(x^2+x+1=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}>0\forall x\)

\(2x^2+x+5=2\left[\left(x+\frac{1}{4}\right)^2+\frac{39}{16}\right]>0\forall x\)

Vậy tập nghiệm của pt là \(S=\varnothing\)

b, \(\frac{x-342}{15}+\frac{x-323}{17}+\frac{x-300}{19}+\frac{x-273}{21}=10\)

\(\Leftrightarrow\left(\frac{x-342}{15}-1\right)+\left(\frac{x-323}{17}-2\right)+\left(\frac{x-300}{19}-3\right)+\left(\frac{x-273}{21}-4\right)=0\)

\(\Leftrightarrow\frac{x-357}{15}+\frac{x-357}{17}+\frac{x-357}{19}+\frac{x-357}{21}=0\)

\(\Leftrightarrow\left(x-357\right)\left(\frac{1}{15}+\frac{1}{17}+\frac{1}{19}+\frac{1}{21}\right)=0\)

\(\Leftrightarrow x-357=0\Leftrightarrow x=357\) 

Vậy tập nghiệm của pt: \(S=\left\{357\right\}\)