Hình như ở đường thẳng thứ 2 bạn bị thiếu mất y thì phải. Nếu vậy thì cách làm như sau:

Ta viết lại các đường thẳng :

(d₁): \(y=\dfrac{-5}{11}x+\dfrac{8}{11}\); (d₂): \(y=\dfrac{-4m}{2m-1}x+\dfrac{m+2}{2m-1}\); (d₃): \(y=\dfrac{10}{7}x-\dfrac{74}{7}\)

Hoành độ giao điểm 2 đường thẳng (d₁) và (d₃) là nghiệm của phương trình: \(\dfrac{-5}{11}x+\dfrac{8}{11}=\dfrac{10}{7}x-\dfrac{74}{7}\) \(\Leftrightarrow\left(-5\right)x\cdot7+8\cdot7=10x\cdot11-74\cdot11\)

\(\Leftrightarrow-35x+56=110x-814\) \(\Leftrightarrow110x+35x=56+814\Leftrightarrow145x=870\) 

\(\Leftrightarrow x=6\) \(\Rightarrow y=-\dfrac{5}{11}\cdot6+\dfrac{8}{11}=-2\) (Thay giá trị của x vừa tìm được vào phương trình đường thẳng (d₁) \(\Rightarrow\) Hai đường thẳng cắt nhau tại điểm I(6;-2) 

Để 3 đường thẳng đồng quy \(\Leftrightarrow\) Đường thẳng (d₂) cũng đi qua điểm I(6;-2) \(\Rightarrow\) \(-2=-\dfrac{4m}{2m-1}\cdot6+\dfrac{m+2}{2m-1}\) \(\Leftrightarrow-2=\dfrac{-24m+m+2}{2m-1}\Leftrightarrow-2=\dfrac{-23m+2}{2m-1}\Leftrightarrow2=\dfrac{23m-2}{2m-1}\Rightarrow4m-2=23m-2\Leftrightarrow23m-4m=2-2\)

19m=0\(\Leftrightarrow m=0\) Vậy ...

\(\left(d1\right),\left(d2\right),\left(d3\right)đồngquy\)

\(\left\{{}\begin{matrix}5x+11y=8\\10x-7y=74\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=-2\end{matrix}\right.\)

Thay : x vào (d2) 

\(\Rightarrow6\cdot4m+\left(2m-1\right)=m+2\)

\(\Rightarrow m=\) \(0.12\)

Tọa độ giao điểm của ( d 1 ) và ( d 2 ) là nghiệm của hệ phương trình:

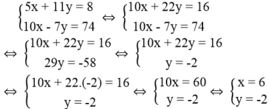
Tọa độ giao điểm của ( d 1 ) và ( d 2 ) là (x; y) = (6; -2)

Để ba đường thẳng ( d 1 ), ( d 2 ), ( d 3 ) đồng quy thì ( d 3 ) phải đi qua giao điểm của ( d 1 ) và ( d 2 ), nghĩa là (x; y) = (6; -2) nghiệm đúng phương trình đường thẳng ( d 3 ).

Khi đó ta có: 4m.6 + (2m – 1).(-2) = m + 2

⇔ 24m – 4m + 2 = m + 2 ⇔ 19m = 0 ⇔ m = 0

Vậy với m = 0 thì 3 đường thẳng ( d 1 ), ( d 2 ), ( d 3 ) đồng quy.

giúp với

Xét hệ pt : \(\left\{{}\begin{matrix}5x+11y=8\left(1\right)\\10x-7y=74\left(2\right)\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}10x+22y=16\left(1\right)\\10x-7y=74\left(2\right)\end{matrix}\right.\)

Trừ 2 vế pt (1) cho pt (2), ta dược :

29y = -58 ⇔ y = -2

Thay y= -2 vào pt (2), ta dược:

10x + 14 = 74 ⇔ x = 6

Thay x = 6, y = -2 vào pt (3), ta dược:

24m -2(2m-1) = m + 2

⇔ 24m - 4m + 2 = m + 2

⇔ 19m = 0

⇔ m = 0

Vậy m = 0 thì 3 đường thẳng đồng qui

(d1):5x+11y=8 => y=\(\frac{8-5x}{11}\)

(d2): 4mx+(2m-1)y=m+2=> y=\(\frac{m+2-4mx}{2m-1}\)

(d3): 10x-7y=74=> y=\(\frac{10x-74}{7}\)

xét phương trình hoành độ giao điểm của (d1) và (d3) ta có:

\(\frac{8-5x}{11}=\frac{10x-74}{7}\)\(\Leftrightarrow56-35x=110x-814\)

\(\Leftrightarrow145x=870\)\(\Leftrightarrow x=6\)

thay vào (d1) ta có: y=-2

=> điểm (6;-2) là giao điểm của d1 và d3

để 3 đường thẳng d1;d2;d3 đồng quy thì d3 phải đi qua (6;-2)

=> (6;-2) thuộc đường thẳng d3

=>\(\frac{m+2-24m}{2m-1}=-2\) \(\Leftrightarrow-4m+2=-23m+2\) \(\Leftrightarrow m=0\)

vậy m=0 thì 3 đường thẳng đồng quy

Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}5x-17y=8\\15x+7y=82\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}15x-51y=24\\15x+7y=82\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-58y=-58\\5x-17y=8\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=1\\5x=17y+8=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\)

Thay x=5 và y=1 vào (d3), ta được:

\(\left(2m-1\right)\cdot5-2m\cdot1=m+1\)

=>10m-5-2m-m-1=0

=>7m-6=0

=>7m=6

=>\(m=\dfrac{6}{7}\)

d₁ và d₂ đồng quy khi hệ phương trình có nghiệm:

\(\left\{{}\begin{matrix}5x+11y=8\\10x-7y=74\end{matrix}\right.\)

x=6 và y=-2

Thế vào d₃: 4m.6-2(2m-1)=m+2

20m+2=m+2

19m=0 suy ra m=0

m=0 thì 3 đường thẳng đồng quy