Cho hàm số \(y=x^3-\left(m+1\right)x^2+mx+m-1\) với \(m\) là các số nguyên thuộc \(\left[-2020;2020\right]\). Tìm tấc cả các giá trị m thoả mản phương trình có hai cực trị A,B và đường thẳng \(\left(d\right)\) đi qua hai điểm A,B cắt trúc tung và trục hoành tại hai điểm C,D sao cho tam giác OCD vuông cân và có diện tích gấp 3 lần tam giác OAB ( với O là gốc toạ độ ).

Những câu hỏi liên quan
cho hàm số y= \(\frac{2x-1}{\sqrt{mx^4+mx^3+\left(m+1\right)x^2+mx+1}}\).Hỏi có bn giá trị nguyên của m để hàm số xác định với mọi x thuộc R.
ĐKXĐ
\(mx^4+mx^3+\left(m+1\right)x^2+mx+1\)
\(=\left(mx^4+mx^3+mx^2+mx\right)+\left(x^2+1\right)\)
=\(mx\left(x^3+x^2+x+1\right)+\left(x^2+1\right)\)
\(=mx\left(x+1\right)\left(x^2+1\right)+\left(x^2+1\right)\)
\(=\left(x^2+1\right).\left[mx\left(x+1\right)+1\right]>0\left(\forall x\right)\)
\(=>mx^2+mx+1>0\left(\forall x\right)\)
\(=>PT\hept{\begin{cases}mx^2+mx+1=0\left(zô\right)nghiệm\forall x\\m>0\end{cases}}\)
\(\hept{\begin{cases}\Delta< 0\\m>0\end{cases}=>\hept{\begin{cases}m^2-4m< 0\\m>0\end{cases}=>\hept{\begin{cases}m\left(m-4\right)< 0\\m>0\end{cases}=>0< m< 4}}}\)
=> m có 3 giá trị là 1,2,3 nha
https://olm.vn/hoi-dap/detail/249896752542.html?pos=586036211459
giúp mk cả câu này
Cho hàm số y=f(x)=\(\left\{{}\begin{matrix}2x^3-3\left(m+1\right)x^2+6mx-2\left(x< =3\right)\\nx+46\left(x>3\right)\end{matrix}\right.\)
trong đó m,n thuộc R. Tính tổng tất cả các giá trị nguyên của tham số m để hàm số y=f(x) có đúng ba điểm cực trị
- Với \(x< 3\Rightarrow f'\left(x\right)=6x^2-6\left(m+1\right)x+6m=6\left(x-1\right)\left(x-m\right)\)
\(f'\left(x\right)=0\Rightarrow6\left(x-1\right)\left(x-m\right)=0\left(1\right)\Rightarrow\left[{}\begin{matrix}x=1\\x=m\end{matrix}\right.\) có tối đa 2 cực trị khi \(x< 3\)
- Với \(x>3\Rightarrow f'\left(x\right)=n\) là hằng số \(\Rightarrow f\left(x\right)\) ko có cực trị khi \(x>3\)
\(\Rightarrow\) Hàm có đúng 3 điểm cực trị khi và chỉ khi nó đồng thời thỏa mãn:
ĐK1: \(f'\left(x\right)=0\) có 2 nghiệm pb khi \(x< 3\Rightarrow\left\{{}\begin{matrix}m< 3\\m\ne1\end{matrix}\right.\)
ĐK2: \(x=3\) là 1 cực trị của hàm số
\(\Rightarrow f\left(x\right)\) liên tục tại \(x=3\) đồng thời đạo hàm đổi dấu khi đi qua \(x=3\)
\(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^-}f\left(x\right)\Leftrightarrow3n+46=25-9m\Rightarrow n=-3m-7\) (2)
Mặt khác do 2 nghiệm của (1) đều nhỏ hơn 3 \(\Rightarrow\) tại lân cận trái của \(x=3\) đạo hàm luôn có dấu dương
\(\Rightarrow\) Để đạo hàm đổi dấu khi đi qua \(x=3\) thì \(f'\left(3^+\right)=n< 0\)
Thế vào (2) \(\Rightarrow-3m-7< 0\Rightarrow m>-\dfrac{7}{3}\)
\(\Rightarrow-\dfrac{7}{3}< m< 3\Rightarrow\sum m=0\)
Đúng 0
Bình luận (0)
Cho hàm số f(x) = \(\dfrac{x^3}{3}-mx^2+\left(m+2\right)x+3\). Có tất cả các giá trị nguyên của tham số m để f'(x) ≥ 0 với mọi thuộc R.
cho hàm số \(f\left(x\right)=mx^2-2x-1\),với m là tham số.Có bao nhiêu số nguyên của \(m\in\left(-10;10\right)\) để \(f\left(x\right)\le0\) với mọi x\(\in\)R
Với \(m=0\Rightarrow f\left(x\right)=-2x-1\le0\Leftrightarrow x\ge-\dfrac{1}{2}\)
\(\Rightarrow m=0\) không thỏa mãn yêu cầu bài toán.
Với \(m\ne0\), \(f\left(x\right)\le0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta'=1+m\le0\end{matrix}\right.\Leftrightarrow m\le-1\)
\(\Rightarrow m\in\left\{m\in Z|-10< m\le-1\right\}\)
Vậy có 9 số nguyên thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Cho hàm số y= \(\dfrac{x^3}{3}-\left(m-1\right)x^2+3\left(m-1\right)x+1\) . Số các giá trị nguyên của m để hàm số đồng biến trên (1;dương vô cực ) là
Cho hàm số ymx+3 có đồ thị là left(d_1right) và hàm số ydfrac{-1}{m}x+3left(mne0right) có đồ thị là left(d_2right)
1) Với m 1
a) Vẽ đồ thị left(d_1right) và left(d_2right) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của left(d_1right) và left(d_2right).
Đọc tiếp
Cho hàm số \(y=mx+3\) có đồ thị là \(\left(d_1\right)\) và hàm số \(y=\dfrac{-1}{m}x+3\left(m\ne0\right)\) có đồ thị là \(\left(d_2\right)\)
1) Với m = 1
a) Vẽ đồ thị \(\left(d_1\right)\) và \(\left(d_2\right)\) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\).
Với m = 1
(d1) có dạng y = x + 3
(d2) có dạng y = -x + 3
Phương trình hoành độ giao điểm
-x + 3 = x + 3
<=> x = 0
Với x = 0 <=> y = 3
Tọa độ giao điểm A(0;3)
Đúng 1
Bình luận (0)
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Số các giá trị nguyên trong đoạn [-100;100] để hàm số y = \(mx^3+mx^2+\left(m+1\right)x-3\) nghịch biến trên R
cho y=\(\dfrac{1}{3}\left(m+1\right)x^3-\left(m+1\right)x^2-mx+1\) ddimnhj tham số m để y'>0 với mọi x thuộc n
\(y'=\left(m+1\right)x^2-2\left(m+1\right)x-m\)
\(m=-1\Rightarrow y'=1>0\forall x\in R\)
\(m\ne-1\Rightarrow y'>0\Leftrightarrow\left\{{}\begin{matrix}m+1>0\\\Delta'< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-1\\\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}< 0\left(vl\right)\end{matrix}\right.\)
Vậy với m=-1 thì...
Đúng 0
Bình luận (0)
Cho hàm số ymx+3 có đồ thị là left(d_1right) và hàm số ydfrac{-1}{m}x+3left(mne0right) có đồ thị left(d_2right)1) Với m 1 a) Vẽ đồ thị left(d_1right) và left(d_2right) trên cùng một mặt phẳng tọa độ b) Tìm tọa độ giao điểm của left(d_1right) và left(d_2right).
Đọc tiếp
Cho hàm số \(y=mx+3\) có đồ thị là \(\left(d_1\right)\) và hàm số \(y=\dfrac{-1}{m}x+3\left(m\ne0\right)\) có đồ thị \(\left(d_2\right)\)
1) Với m = 1
a) Vẽ đồ thị \(\left(d_1\right)\) và \(\left(d_2\right)\) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\).
1: Khi m=1 thì (d1): y=x+3 và (d2): y=-x+3
a: 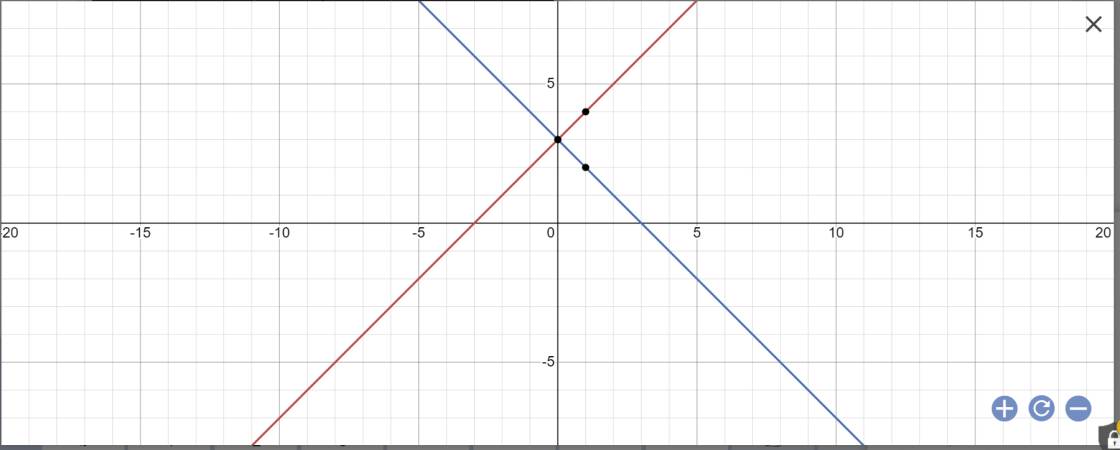
b: Tọa độ giao điểm là:
x+3=-x+3 và y=x+3
=>x=0 và y=3
Đúng 2
Bình luận (0)





















