Tìm x biết pi+k2pi/3 trong đó pi khác kpi/2
Những câu hỏi liên quan
Phương trình 1+2cosx=2 có tập nghiệm là: a.x=pi/3+k2pi b.x=pi+k2pi C.x=-pi/3+k2pi d.x=+- pi/3+k2pi
\(1+2cosx=2\Leftrightarrow cosx=\dfrac{1}{2}\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{3}+k2\pi\)
Đúng 2
Bình luận (0)
Phương trình
1+sinx.sin2x - cosx.sin^2 2x= 2 .cos^2 (pi/4-x ) có hai nghiệm có dạng x= anpha + k2pi và x= beta +kpi/2
Khi đó anpha+beta =?
1) Goi alpha la so do cua 1 cung luong giac co diem dau A, diem cuoi B. Khi do so do cua cac cung luong giac bat ki co diem dau A, diem cuoi B bang
A. pi - alpha + k2pi, k thuoc Z
B. alpha + kpi, k thuoc Z
C. alpha + k2pi, k thuoc Z
D. -alpha + k2pi, k thuoc Z
câu 29 : Nghiệm của pt cotx=-căn 3 trên 3 ?
câu 30 nghiệm của phương trình cot(x+pi/3)= căn 3 có dạng x = -pi/n -kpi/m (k thuộc z ) . khi đó n-m bằng ?
câu 31 phương trình cot (2x + pi/6) =1 có họ nghiệm dạng x =alpha + kpi/2 (k thuoc z):alpha thuoc (0 :pi/2) khi đó giá trị gần nhất của m là bnh ?>
Tính sin ( pi/6 +k2pi/3 )
5.msinx=sĩn2+sin3x
tìm m để pt có nghiệm
a. x khác kpi
b.x khác 2kpi
c.x thuộc (pi/2;pi)
khó quá đi ; mà hình như nó gần dúng như bài 4 bạn đăng á !!
Mk ko bk nữa
Đúng 0
Bình luận (0)
Tập xác định của hàm số y=cotx/cosx-1 A . R\{kpi/2 , k thuộc z} B . R\{pi/2+kpi,k thuộc z} C . R\{kpi,k thuộc z} D . R
\(y=\dfrac{cotx}{cosx-1}\)
Đk:\(cosx-1\ne0\Leftrightarrow cosx\ne1\)\(\Leftrightarrow x\ne k\pi,k\in Z\)
\(D=R\backslash\left\{k\pi;k\in Z\right\}\)
Ý C
Đúng 1
Bình luận (1)
SGK Kết nối tri thức và cuộc sống
17 tháng 8 2023 lúc 16:44
Cho hàm số \(f(x) = {x^2} + {\sin ^3}x\). Khi đó \(f'\left( {\frac{\pi }{2}} \right)\) bằng
A. \(\pi \).
B. \(2\pi \).
C. \(\pi + 3\).
D. \(\pi - 3\).
\(f'\left(x\right)=2x+3sin^2\left(x\right)cos\left(x\right)\\ \Rightarrow f'\left(\dfrac{\pi}{2}\right)=\pi\)
\(\Rightarrow\) Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số y cot xa) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:xfrac{pi }{6}frac{pi }{4}frac{pi }{2}frac{{3pi }}{4}frac{{5pi }}{6}y cot x?????b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; cotx) với x in left( {0;pi } right) và nối lại ta được đồ thị hàm số y cot x trên khoảng left( {0;pi } right) (Hình 31)c) Làm tương tự như trên đối với các khoảng left( {pi ;2pi } right),left( { -...
Đọc tiếp
Cho hàm số \(y = \cot x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
x | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\frac{{5\pi }}{6}\) |
\(y = \cot x\) | ? | ? | ? | ? | ? |
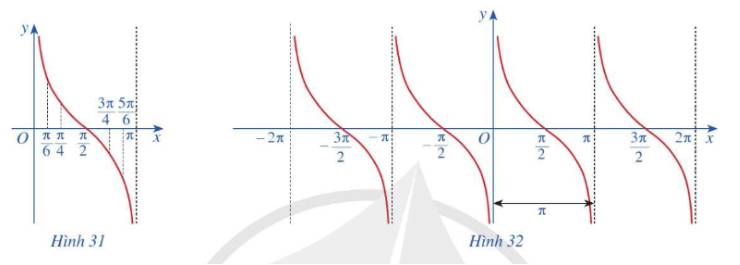
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; cotx) với \(x \in \left( {0;\pi } \right)\) và nối lại ta được đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) (Hình 31)
c) Làm tương tự như trên đối với các khoảng \(\left( {\pi ;2\pi } \right),\left( { - \pi ;0} \right),\left( { - 2\pi ; - \pi } \right),....\)ta có đồ thị hàm số \(y = \cot x\)trên E được biểu diễn ở Hình 32.
a)
x | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\frac{{5\pi }}{6}\) |
\(y = \cot x\) | \(\sqrt 3 \) | 1 | 0 | -1 | \( - \sqrt 3 \) |
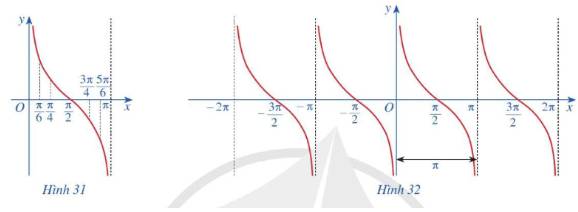
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; cotx) với \(x \in \left( {0;\pi } \right)\) và nối lại ta được đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) (Hình 31)
c) Làm tương tự như trên đối với các khoảng \(\left( {\pi ;2\pi } \right),\left( { - \pi ;0} \right),\left( { - 2\pi ; - \pi } \right),....\)ta có đồ thị hàm số \(y = \cot x\)trên E được biểu diễn ở Hình 32.
Đúng 0
Bình luận (0)