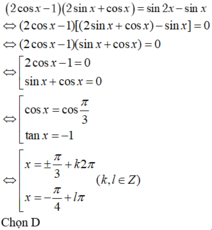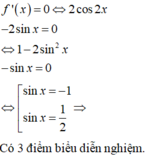Giải phương trình lượng giác: Sin2x × 2cosx + cos3x = 1

Những câu hỏi liên quan
Giải các phương trình sau:
a, cos3x-4cos2x+3cosx-4=0, ∀x∈[0;14]
b, (2cosx-1)(2cos+cosx)=sin2x-sinx
c, cos3x+cos2x+1+sin2x+cos2x=0
a/ \(4cos^3x-3cosx-4\left(2cos^2x-1\right)+3cosx-4=0\)
\(\Leftrightarrow4cos^3x-8cos^2x=0\)
\(\Leftrightarrow4cos^2x\left(cosx-2\right)=0\)
\(\Leftrightarrow cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\)
\(0< \frac{\pi}{2}+k\pi< 14\Rightarrow-\frac{1}{2}< k< \frac{14-\frac{\pi}{2}}{\pi}\Rightarrow k=\left\{0;1;2;3\right\}\)
\(\Rightarrow x=\left\{\frac{\pi}{2};\frac{3\pi}{2};\frac{5\pi}{2};\frac{7\pi}{2}\right\}\)
b/ Bạn coi lại đề, cái ngoặc thứ 2 thiếu \(\left(2cos\left(???\right)+cosx\right)\)
c/ Bạn coi lại đề, có 2 số hạng \(cos2x\) xuất hiện ở vế trái, cấp 3 chắc ko ai cho kiểu vậy đâu, nếu đúng thế thì người ta cộng luôn thành \(2cos2x\) cho rồi
Đúng 0
Bình luận (0)
1) cho góc x thỏa mãn \(cosx=-\dfrac{4}{5}\) và \(\pi< x< \dfrac{3\pi}{2}\) tính \(P=tan\left(x-\dfrac{\pi}{4}\right)\)
2) giải phương trình \(2cosx-\sqrt{2}=0\)
3) phương trình lượng giác \(cos3x=cos\dfrac{\pi}{15}\) có nghiệm là
Giải phương trình :
Cotx=tanx +2cos4x\sin2x
Và
sinx +cos2x - 2cosx×cos3x=0
câu 1
⇒ \(\dfrac{cosx}{sinx}\) - \(\dfrac{sinx}{cosx}\) -\(\dfrac{2cos4x}{2sinxcosx}\) =0
⇔ \(\dfrac{cos^2x-sin^2x}{sinx.cosx}\) -\(\dfrac{cos4x}{sinx.cosx}\)= 0
⇔ \(\dfrac{cos2x-cos4x}{sinx.cosx}\) = 0
\(\left[{}\begin{matrix}cos2x=cos4x\\sin2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=4x+k2\pi\\2x=-4x+k2\pi\\2x=k\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-k\pi\\x=\dfrac{k\pi}{3}\\x=\dfrac{k\pi}{2}\end{matrix}\right.\) (k∈ Z)
Đúng 0
Bình luận (0)
câu 2 dùng công thức biến đổi tích thành tổng thành cos 4x + cos 2x sau đó phương trình trở thành sin x - cos 4x=0
Đúng 0
Bình luận (0)
1)Giải pt bậc hai đối với một hàm số lượng giác:
a. 2 cosxcos2x=1+cos2x+cos3x
b.5(1+cosx)=2+sin^4x-cos^4x
c.sin^4x +cos^4x=sin2x-1/2
2) giải phương trình chứa ẩn dưới mẫu:
Sin2x+2cosx-sinx-1/ tan x+√3=0
Giải các phương trình sau:
a) √3.sin2x - cos2x + 1 = 0
b) 3sin4x + 4cos4x = 1
c) sin3x - √3.cos3x = 2cos5x
d) sinx(sinx + 2cosx) = 2
e) √3(sin2x + cos7x) = sin7x - cos2x
\(\text{c) }sin3x-\sqrt{3}cos3x=2cos5x\\ \Leftrightarrow\frac{1}{2}sin3x-\frac{\sqrt{3}}{2}cos3x=cos5x\\ \Leftrightarrow sin\frac{\pi}{6}\cdot sin3x-cos\frac{\pi}{6}\cdot cos3x=cos5x\\ \Leftrightarrow cos\left(3x+\frac{\pi}{6}\right)=-cos5x\\ \Leftrightarrow cos\left(3x+\frac{\pi}{6}\right)=cos\left(\pi-5x\right)\\ \Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{6}=\pi-5x+m2\pi\\3x+\frac{\pi}{6}=5x-\pi+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{5\pi}{48}+\frac{m\pi}{4}\\x=\frac{7\pi}{12}-n\pi\end{matrix}\right.\)
\(d\text{) }sinx\left(sinx+2cosx\right)=2\\ \Leftrightarrow cos^2x+\left(sinx-cosx\right)^2=0\\ \Leftrightarrow cosx=sinx=0\left(VN\right)\)
\(e\text{) }\sqrt{3}\left(sin2x+cos7x\right)=sin7x-cos2x\\ \Leftrightarrow\sqrt{3}sin2x+cos2x=sin7x-\sqrt{3}cos7x\\ \Leftrightarrow sin2x\cdot\frac{\sqrt{3}}{2}+cos2x\cdot\frac{1}{2}=sin7x\cdot\frac{1}{2}-cos7x\cdot\frac{\sqrt{3}}{2}\\ \Leftrightarrow sin2x\cdot cos\frac{\pi}{3}+cos2x\cdot sin\frac{\pi}{3}=sin7x\cdot cos\frac{\pi}{3}-cos7x\cdot sin\frac{\pi}{3}\\ \Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(7x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=7x-\frac{\pi}{3}+m2\pi\\2x-\frac{\pi}{3}=\frac{4\pi}{3}-7x+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{-m2\pi}{5}\\x=\frac{5\pi}{27}+\frac{n2\pi}{9}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(\text{a) }\sqrt{3}sin2x-cos2x+1=0\\ \Leftrightarrow\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x=-\frac{1}{2}\\ \Leftrightarrow cos\frac{\pi}{3}\cdot cos2x-sin\frac{\pi}{3}\cdot sin2x=\frac{1}{2}\\ \Leftrightarrow cos\left(2x-\frac{\pi}{3}\right)=cos\frac{\pi}{3}\\ \Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{3}+m2\pi\\2x-\frac{\pi}{3}=-\frac{\pi}{3}+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+m\pi\\x=n\pi\end{matrix}\right.\)
\(\text{b) }pt\Leftrightarrow sin4x=\frac{1-4cosx}{3}\\ \Leftrightarrow sin^24x+cos^24x=\left(\frac{1-cos4x}{3}\right)^2+cos^24x=1\\ \Leftrightarrow\left[{}\begin{matrix}cos4x=1\\cos4x=-\frac{4}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}cos4x=1\\cos4x=-\frac{4}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{arccos\left(-\frac{4}{5}\right)}{4}+\frac{k\pi}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
giải phương trình:
(2cosx-1)(2sinx+cosx)=sin2x-sinx
Lời giải:
PT $\Leftrightarrow (2\cos x-1)(2\sin x+\cos x)=2\sin x\cos x-\sin x$
$\Leftrightarrow (2\cos x-1)(2\sin x+\cos x)=\sin x(2\cos x-1)$
$\Leftrightarrow (2\cos x-1)(\sin x+\cos x)=0$
$\Rightarrow 2\cos x=1$ hoặc $\sin x=-\cos x=\cos (\pi -x)=\sin (x-\frac{\pi}{2})$
Đến đây thì đơn giản rồi.
Đúng 3
Bình luận (2)
Giải phương trình (2cosx - 1)(2sinx + cosx) = sin2x - sinx
![]()
![]()
![]()
![]()
Cho hàm số f(x) = sin2x + 2cosx. Số điểm biểu diễn nghiệm của phương trình f’(x)=0 trên đường tròn lượng giác là:
A. 2
B. 3
C. 4
D. Vô số
Cho hàm số f(x)=sin2x+2cosx. Số điểm biểu diễn nghiệm của phương trình f ' ( x ) = 0 trên đường tròn lượng giác là:
A. 2
B. 3
C. 4
D. Vô số