Cho hàm số y = \(\sqrt{x^2-2x+1}\)+ \(\sqrt{x^2-6x+9}\)
vẽ đồ thị hàm số trên
Cho hàm số y= /x+1/+\(\sqrt{x^2-4x+4}\)
a) Vẽ đồ thị hàm số
b) Từ đồ thị hàm số suy ra Min
Giúp em với mn
\(y=\left|x+1\right|+\sqrt{\left(x-2\right)^2}=\left|x+1\right|+\left|x-2\right|\)
\(\Rightarrow\left\{{}\begin{matrix}y=2x-1\text{ với }x\ge2\\y=1-2x\text{ với }x\le-1\\y=3\text{ với }-1\le x\le2\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau (vẽ 3 đồ thị hàm bậc nhất xác định trên trên ở từng khoảng của chúng)
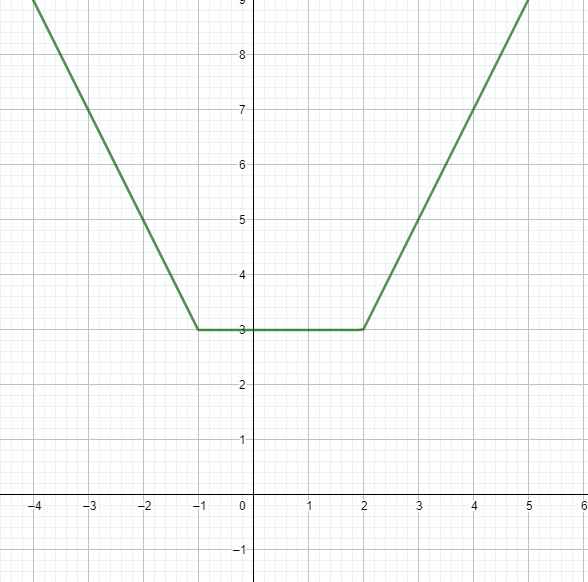
Từ đồ thị \(\Rightarrow y_{min}=3\) khi \(-1\le x\le2\)
Câu 1:
1. Thực hiện phép tính: \(16\sqrt{9}-9\sqrt{16}\)
2. Cho hàm số y = ax\(^2\) với a là tham số
a) Tìm a để đồ thị hàm số qua điểm M (2; 8)
b) Vẽ đồ thị của hàm số ứng với giá trị a tìm được
Câu 2:
1. Giải phương trình và hệ phương trình sau:
a) x\(^2\) - 5x + 4 = 0
b) \(\left\{{}\begin{matrix}3x+2y=8\\2x-y=3\end{matrix}\right.\)
2. Cho phương trình x - 2 (m + 1)x + m - 4 = 0
a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi m
b) Gọi x\(_1\), x\(_2\) là hai nghiệm của phương trình đã cho. Chứng minh giá trị biểu thức A = x\(_1\)(1 - x\(_2\)) + x\(_2\) (1 - x\(_1\)) không phụ thuộc m
Câu 1:
1: Ta có: \(16\sqrt{9}-9\sqrt{16}\)
\(=16\cdot3-9\cdot4\)
\(=48-36=12\)
2:
a) Thay x=2 và y=8 vào hàm số \(y=a\cdot x^2\), ta được:
\(a\cdot2^2=8\)
\(\Leftrightarrow4a=8\)
hay a=2
Vậy: a=2
Câu 2:
1:
a) Ta có: \(x^2-5x+4=0\)
\(\Leftrightarrow x^2-x-4x+4=0\)
\(\Leftrightarrow x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
Vậy: S={1;4}
Cho hàm số y = x2 - 2x - 3, có đồ thị là P
1, Lập bảng biến thiên và vè đồ thị hàm số trên
2, Dựa vaov đồ thị p, tìm m sao cho pt \(\sqrt{x^2-x-m}=\sqrt{x+1}\)có nghiệm
Mình cảm ơn
Mọi người ơi cho mình hỏi bài này với ạ
1.Số đường tiệm cận của hàm số y=\(\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}\) là
2.Tìm tất cả các tiệm cận đứng của đồ thị hàm số y=\(\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}\)
Mình cảm ơn mọi người nhiều lắm !!!!!
1.
Điều kiện xác định của căn thức: \(\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{1-1}{1}=0\Rightarrow y=0\) là 1 TCN
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{-1-1}{-1}=2\Rightarrow y=2\) là 1 TCN
\(\lim\limits_{x\rightarrow-5}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{\sqrt{26}+5}{0}=+\infty\Rightarrow x=-5\) là 1 TCĐ
\(\lim\limits_{x\rightarrow5}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{\sqrt{26}-5}{0}=+\infty\Rightarrow x=5\) là 1 TCĐ
Hàm có 4 tiệm cận
2.
Căn thức của hàm luôn xác định
Ta có:
\(\lim\limits_{x\rightarrow2}\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}=\lim\limits_{x\rightarrow2}\dfrac{\left(2x-1\right)^2-\left(x^2+x+3\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(3x+1\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{3x+1}{\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}=\dfrac{-7}{6}\) hữu hạn
\(\Rightarrow x=2\) ko phải TCĐ
\(\lim\limits_{x\rightarrow3}\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}=\dfrac{5-\sqrt{15}}{0}=+\infty\)
\(\Rightarrow x=3\) là tiệm cận đứng duy nhất
Cho hàm số \(y=\sqrt{x^2-4x+4}-\sqrt{x^2+4x+4}\)
a) Vẽ đồ thị hàm số
b) Dùng đồ thị hàm số tìm giá trị max của y, giá trị min của y
Bài 1. Cho hàm số
y= 2x-1
a) Tính giá trị của hàm số y khi x=0; x=1; x= -2
b) Tìm giá trị của x khi y=3
Bài 2. Cho hàm số
y= -3x
a) Vẽ đồ thị hàm số
b) Tìm trên đồ thị hàm số điểm có hoành độ bằng 2
c) Tìm trên đồ thị hàm số điểm có tung độ bằng -6
Bài 1:
a: x=0 => y=-1
x=1 =>y=1
Tính các đạo hàm của hàm số sau:
a) \(y=\sqrt{x}\left(x+3\right)\)
b) \(y=\sqrt{2x^2-6x-9}\)
c) \(y=\left(\sqrt{x^2+1}+x\right)^{10}\)
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Cho hàm số \(y=\sqrt{x^2-4x+4}-\sqrt{x^2+4x+4}\)
a) Vẽ đồ thị hàm số
b) Dùng đồ thị tìm giá trị max của y, giá trị min của y
Cho hàm số y=2x+m (d)
1)Tìm m để đồ thị hàm số (d) đi qua:
a)A(-1;3)
b)B(\(\sqrt{2}\);\(-5\sqrt{2}\))
2)Tìm m để đồ thị hàm số (d) cắt đồ thị hàm số y=3x-2 trong góc phần tư thứ tư
a: Thay x=1 và y=3 vào (d), ta được:
m+2=3
hay m=1
Bài 1:
a. Để $(d)$ đi qua $A(-1;3)$ thì:
$y_A=2x_A+m\Leftrightarrow 3=2(-1)+m$
$\Leftrightarrow m=5$
b. Để $(d)$ đi qua $B(\sqrt{2}; -5\sqrt{2})$ thì:
$y_B=2x_B+m$
$\Leftrightarrow -5\sqrt{2}=2\sqrt{2}+m$
$\Leftrightarrow m=-7\sqrt{2}$
Bài 2:
PT hoành độ giao điểm:
$2x+m=3x-2$
$\Leftrightarrow m+2=x$
$y=3x-2=3(m+2)-2=3m+4$
Vậy tọa độ của 2 đths là $(m+2, 3m+4)$
Để 2 đths cắt nhau tại góc phần tư thứ nhất thì \(\left\{\begin{matrix} m+2>0\\ 3m+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>-2\\ m> \frac{-4}{3}\end{matrix}\right.\Leftrightarrow m> \frac{-4}{3}\)