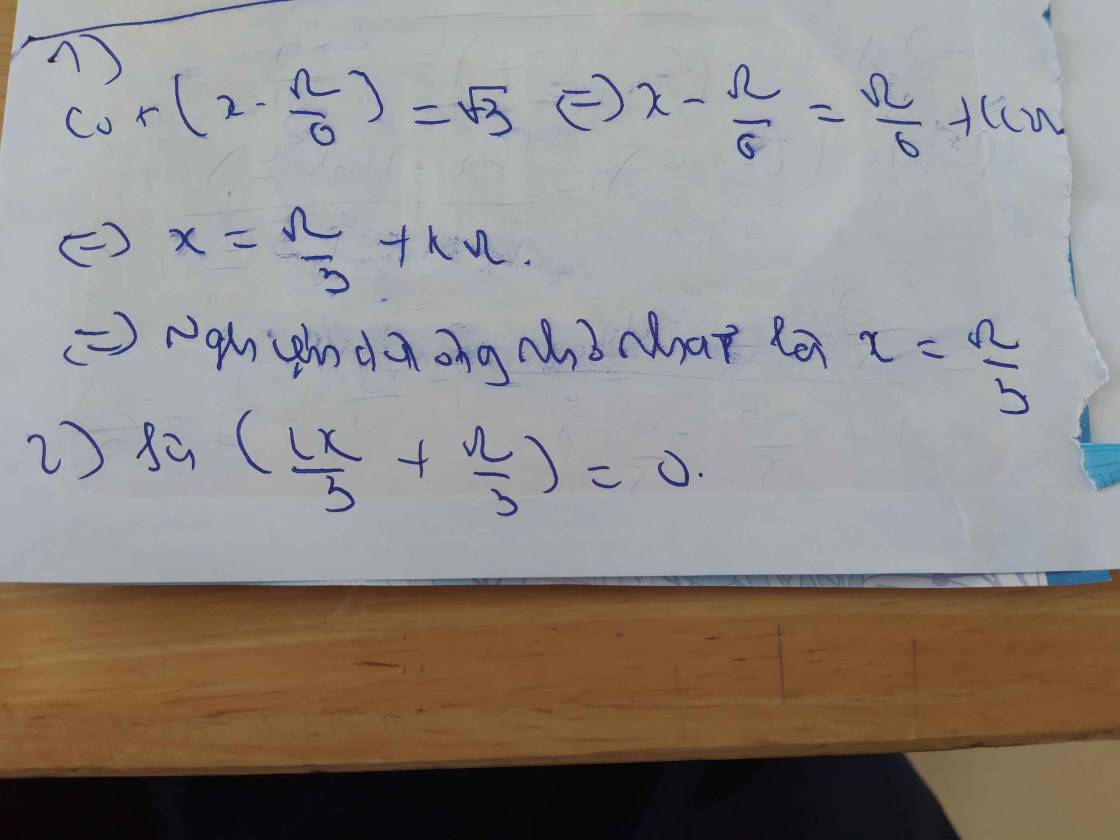=>(2x+3)^2-5x(2x+3)=0

=>(2x+3)(-3x+3)=0

=>x=-3/2 hoặc x=1

=>Nghiệm lớn nhất là x=1

\(x^2\left(x+2a\right)-\left(a+1\right)^2\left(x+2a\right)=0\)

\(\Leftrightarrow\left(x+2a\right)\left[x^2-\left(a+1\right)^2\right]=0\)

\(\Leftrightarrow\left(x+2a\right)\left(x+a+1\right)\left(x-a-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2a\\x=-a-1\\x=a+1\end{matrix}\right.\) 

Pt đã cho luôn có 3 nghiệm (như trên) với mọi a

\(\left\{{}\begin{matrix}-a-1-\left(-2a\right)=a-1< 0\\\left(-a-1\right)-\left(a+1\right)=-2\left(a+1\right)< 0\\\end{matrix}\right.\)

\(\Rightarrow x=-a-1\) là nghiệm nhỏ nhất

\(x^3+3x^2+2x=0\Rightarrow x\left(x+1\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=-2\end{matrix}\right.\)

\(\left(x+1\right)\left(x^2+2x+1+a\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+1=-a\end{matrix}\right.\)

Vì 2 pt đã có nghiệm chung là \(-1\Rightarrow\) nghiệm của pt \(\left(x+1\right)^2=-a\) phải khác \(0,2\)

\(\Rightarrow a\ne-1;-9\)

(cách mình là vậy chứ mình cũng ko chắc là có đúng ko nữa)

\(x^3+3x^2+2x=0\left(1\right)\)

\(\Leftrightarrow x\left(x^2+3x+2\right)=0\)

\(\Leftrightarrow x\left(x^2+x+2x+2\right)=0\)

\(\Leftrightarrow x\left[x\left(x+1\right)+2\left(x+1\right)\right]=0\)

\(\Leftrightarrow x\left(x+2\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\\x+1=0\end{matrix}\right.\)            \(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-1\end{matrix}\right.\)

Vậy phương trình (1) có nghiệm \(x=0;x=-2;x=-1\)

\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+1+a\right)=0\left(2\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\Leftrightarrow x=-1\\x^2+2x+1+a=0\end{matrix}\right.\)

\(\Rightarrow x=-1\) là (1) nghiệm của phương trình (2)

Đặt \(F\left(x\right)=\left(x+1\right)\left(x^2+2x+1+a\right)\)

Có phương trình (1) và (2) có nghiệm chung là =1

Để (1) và (2) có 1 nghiệm chung duy nhất 

Thì \(\left\{{}\begin{matrix}F\left(0\right)\ne0\\F\left(-2\right)\ne0\end{matrix}\right.\)              \(\Leftrightarrow\left\{{}\begin{matrix}1.\left(1+a\right)\ne0\\\left(-2+1\right)\left(4-4+1+a\right)\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a\ne-1\\-\left(a+1\right)\ne0\end{matrix}\right.\)            \(\Leftrightarrow\left\{{}\begin{matrix}a\ne-1\\a\ne-1\end{matrix}\right.\)

-Chúc bạn học tốt-

\(\cos5x=-\sin4x\)

<=> \(\cos5x=\cos\left(4x+\frac{\pi}{2}\right)\)

\(\Leftrightarrow\orbr{\begin{cases}5x=4x+\frac{\pi}{2}+k2\pi\\5x=-4x-\frac{\pi}{2}+k2\pi\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}}\)

Nghiệm âm lớn nhất: \(-\frac{\pi}{18}\)

Nghiệm dương  nhỏ nhất: \(\frac{\pi}{2}\)

pt <=> \(\sin\left(5x+\frac{\pi}{3}\right)=\sin\left(2x-\frac{\pi}{3}+\frac{\pi}{2}\right)\)

<=> \(\sin\left(5x+\frac{\pi}{3}\right)=\sin\left(2x+\frac{\pi}{6}\right)\)

<=> \(\orbr{\begin{cases}5x+\frac{\pi}{3}=2x+\frac{\pi}{6}+k2\pi\\5x+\frac{\pi}{3}=\pi-2x-\frac{\pi}{6}+k2\pi\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{\pi}{18}+\frac{k2\pi}{3}\\x=\frac{\pi}{14}+\frac{k2\pi}{7}\end{cases}}\)

Trên \(\left[0,\pi\right]\)có các nghiệm:

\(\frac{11\pi}{18},\frac{\pi}{14},\frac{5\pi}{14},\frac{9\pi}{14},\frac{13\pi}{14}\)

tính tổng:...

\(\left(2x^2+3\right)^2-10x^2-15x=0\)

\(\Leftrightarrow4x^4+12x^2+9-10x^2-15x=0\)

\(\Leftrightarrow4x^4+2x^2-15x+9=0\)

\(\Leftrightarrow4x^4-4x^2+6x^2-6x-9x+9=0\)

\(\Leftrightarrow4x^2\left(x^2-1\right)+6x\left(x-1\right)-9\left(x-1\right)=0\)

\(\Leftrightarrow4x^2\left(x-1\right)\left(x+1\right)+6x\left(x-1\right)-9\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left[4x\left(x+1\right)+6x-9\right]=0\)

\(\Leftrightarrow\left(x-1\right)\left(4x^2+10x-9\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(4x^2+10x+\frac{25}{4}+\frac{11}{4}\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left[\left(2x+\frac{5}{2}\right)^2+\frac{11}{4}\right]=0\)

Vì \(\left(2x+\frac{5}{2}\right)^2+\frac{11}{4}>0\)

=> x - 1 = 0

=> x = 1 

Vậy x = 1

1.

Đặt \(f\left(x\right)=\left(m^2+1\right)x^3-2m^2x^2-4x+m^2+1\)

\(f\left(x\right)\) xác định và liên tục trên R

\(f\left(x\right)\) có bậc 3 nên có tối đa 3 nghiệm (1)

\(f\left(0\right)=m^2+1>0\) ; \(\forall m\)

\(f\left(1\right)=\left(m^2+1\right)-2m^2-4+m^2+1=-2< 0\) ;\(\forall m\)

\(\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (2)

\(f\left(2\right)=8\left(m^2+1\right)-8m^2-8+m^2+1=m^2+1>0\)

\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) (3)

\(f\left(-3\right)==-27\left(m^2+1\right)-18m^2+12+m^2+1=-44m^2-14< 0\)

\(\Rightarrow f\left(-3\right).f\left(0\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-3;0\right)\) (4)

Từ (1); (2); (3); (4) \(\Rightarrow f\left(x\right)=0\) có đúng 3 nghiệm phân biệt

2.

Đặt \(t=g\left(x\right)=x.cosx\)

\(g\left(x\right)\) liên tục trên R và có miền giá trị bằng R \(\Rightarrow t\in\left(-\infty;+\infty\right)\)

\(f\left(t\right)=t^3+m\left(t-1\right)\left(t+2\right)\)

Hàm \(f\left(t\right)\) xác định và liên tục trên R

\(f\left(1\right)=1>0\)

\(f\left(-2\right)=-8< 0\)

\(\Rightarrow f\left(1\right).f\left(-2\right)< 0\Rightarrow f\left(t\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)

\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm với mọi m

3. Chắc ngoặc thứ là \(\left(2m^2-2m+4040\right)\) ?

\(\Leftrightarrow\left(m^2-m+2021\right)x^3-2\left(m^2-m+2020\right)x^2-4x+m^2-m+2021=0\)

Do \(m^2-m+2020>0\), đặt \(m^2-m+2020=n^2\)

\(\Rightarrow\left(n^2+1\right)x^3-2n^2x^2-4x+n^2+1=0\)

Quy về bài số 1