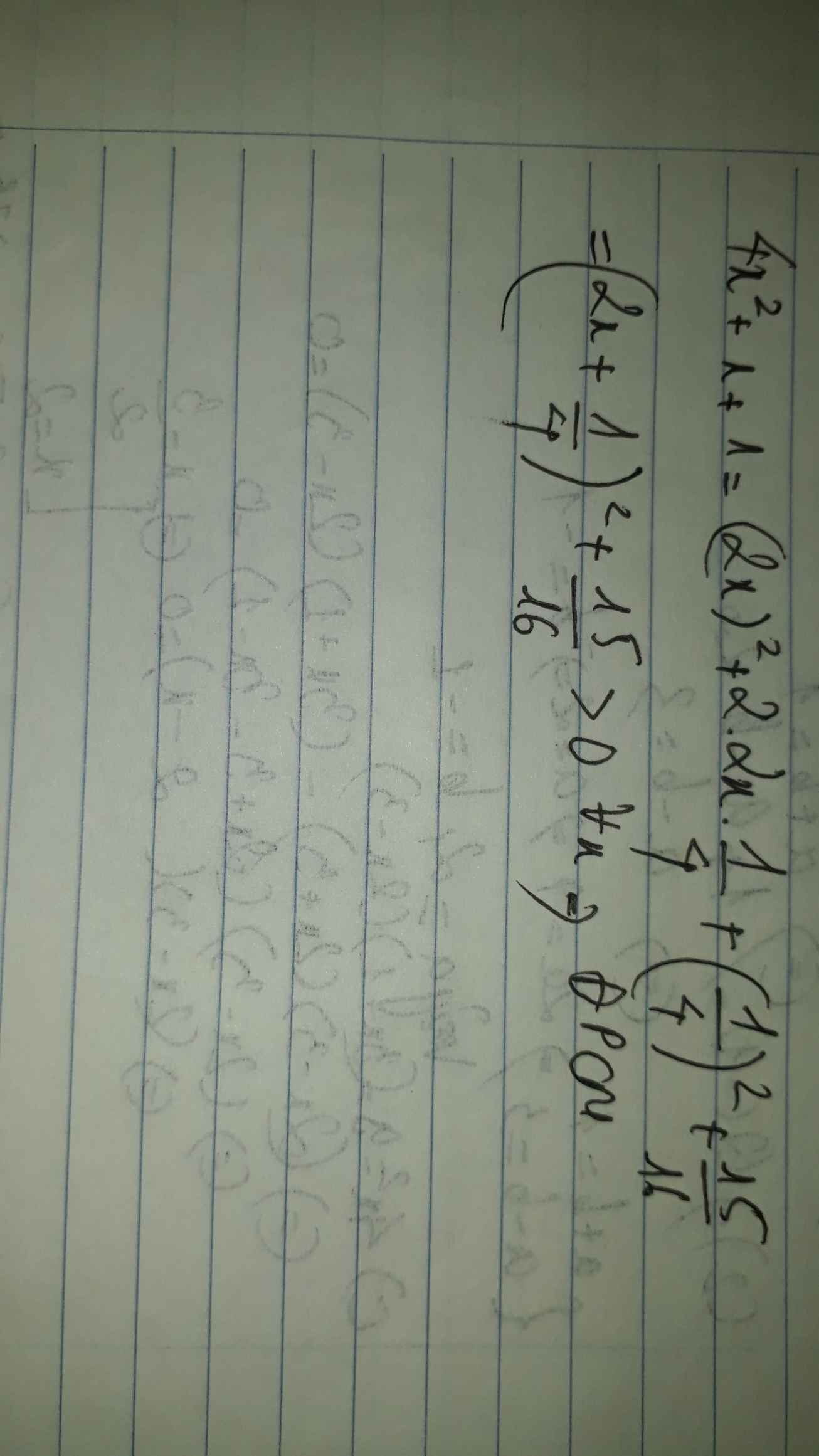Chứng minh: \(-x^2+3x-4< 0\) với mọi số thực x

Những câu hỏi liên quan
Chứng minh -x2 + 3x - 4 < 0 với mọi số thực x
Ta có: \(-x^2+3x-4\)
\(=-\left(x^2-3x+4\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\right)\)
\(=-\left(x-\dfrac{3}{2}\right)^2-\dfrac{7}{4}< 0\forall x\)
Đúng 2
Bình luận (0)
$-x^2+3x-4\\=-x^2+2.x.\dfrac{3}{2}-\dfrac{9}{4}-\dfrac{7}{4}\\=-(x-\dfrac{3}{2})^2-\dfrac{7}{4}<0$
=> ĐPCM
Đúng 1
Bình luận (0)
Chứng minh rằng : 3x2-6x+4 >0 với mọi số thực x.
chứng minh x^2-3x+5>0, với mọi số thực x
\(x^2-3x+5=\left(x-\frac{3}{2}\right)^2+\frac{11}{4}\ge\frac{11}{4}>0\) với mọi số thực x
Đúng 0
Bình luận (0)
chứng minh 9x-3x^2-12<0 với mọi số thực x
-3x^2+9x-12
=-3(x^2-3x+4)
=-3(x^2-3x+9/4+7/4)
=-3(x-3/2)^2-21/4<0
Đúng 0
Bình luận (0)
Chứng minh:- x^2 + 3x - 4 < 0 với mọi số thực x
Tính A= x^16 - 10x^15 + 10x^14- 10x^13 + ....+ 10x^2 - 10x = 10 với x=9
---- Mấy bn giải nhanh bài này dùm mk với!!!
chứng minh rằng :
a)x2-x+1<0 với mọi số thực x
b)-x2+2x-4<0 với mọi số thực x
a) Đề sai thì phải.Phải là CM: \(x^2-x+1>0\) với mọi x
Ta có:
\(x^2-x+1=\left(x^2-x+\frac{1}{4}\right)+\frac{3}{4}\)
\(=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\) nên \(\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0\)
Vậy \(x^2-x+1>0\) với mọi \(x\in R\)
b)Ta có:
\(-x^2+2x-4=-\left(x^2-2x+1\right)-3\)
\(=-\left(x-1\right)^2-3\)
Vì \(-\left(x-1\right)^2\le0\) với mọi x nên \(-\left(x-1\right)^2-3< 0\)
Vậy \(-x^2+2x-4< 0\) với mọi \(x\in R\)
chứng minh biểu thức 4\(x^2\) + x + 1 > 0 với mọi số thực x
\(4x^2+x+1=3x^2+x^2+x+\dfrac{1}{4}+\dfrac{3}{4}=3x^2+\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\in R\)
Đúng 1
Bình luận (0)
Ta có: \(4x^2+x+1\)
\(=\left(2x\right)^2+2\cdot2x\cdot\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{15}{16}\)
\(=\left(2x+\dfrac{1}{4}\right)^2+\dfrac{15}{16}>0\forall x\)
Đúng 1
Bình luận (0)
Chứng Minh rằng:
\(A=x^2-3x+3>0,B=x^2-2x+9y^2-y+3>0\) với mọi số thực x,y
Lời giải:
\(A=x^2-3x+3=\left(x-\frac{3}{2}\right)^2+\frac{3}{4}\geq 0+\frac{3}{4}\Leftrightarrow A\geq \frac{3}{4}>0\)
Do đó ta có đpcm.
\(B=x^2-2x+9y^2-y+3\)
\(\Leftrightarrow B=(x^2-2x+1)+(9y^2-y+\frac{1}{36})+\frac{71}{36}\)
\(\Leftrightarrow B=(x-1)^2+\left(3y-\frac{1}{6}\right)^2+\frac{71}{36}\geq 0+0+\frac{71}{36}\)
\(\Leftrightarrow B\geq \frac{71}{36}>0\) (đpcm)
Đúng 0
Bình luận (1)
Chứng minh:
a) \(x^2-4xy+4y^2+3>0\)với mọi số thực x và y
b) \(3x-x^2-3<0\)với mọi số thực x
ai ủng hộ 9 li-ke tròn 100 Điểm hỏi đáp , thanks trước nha
Đúng 0
Bình luận (0)