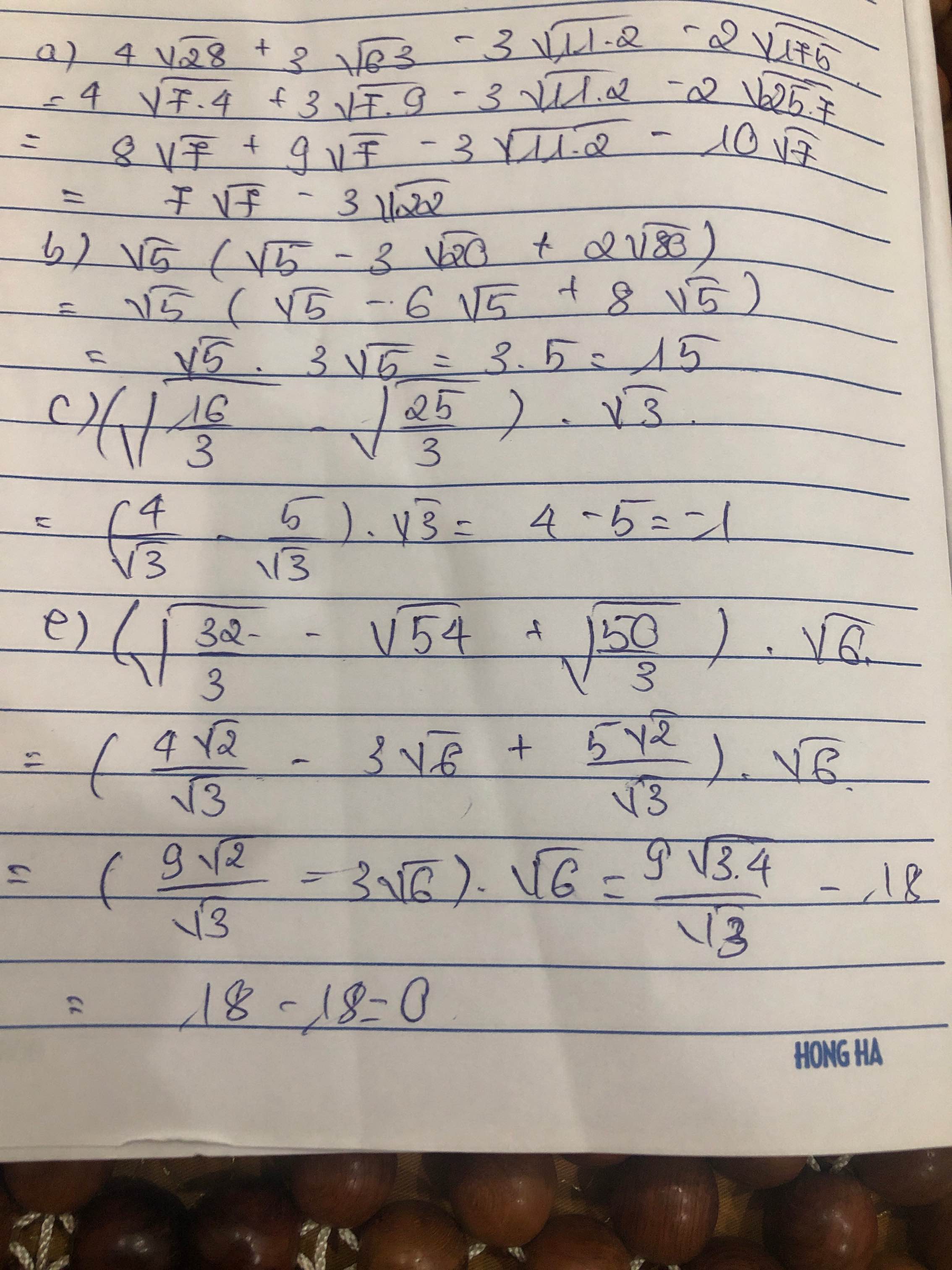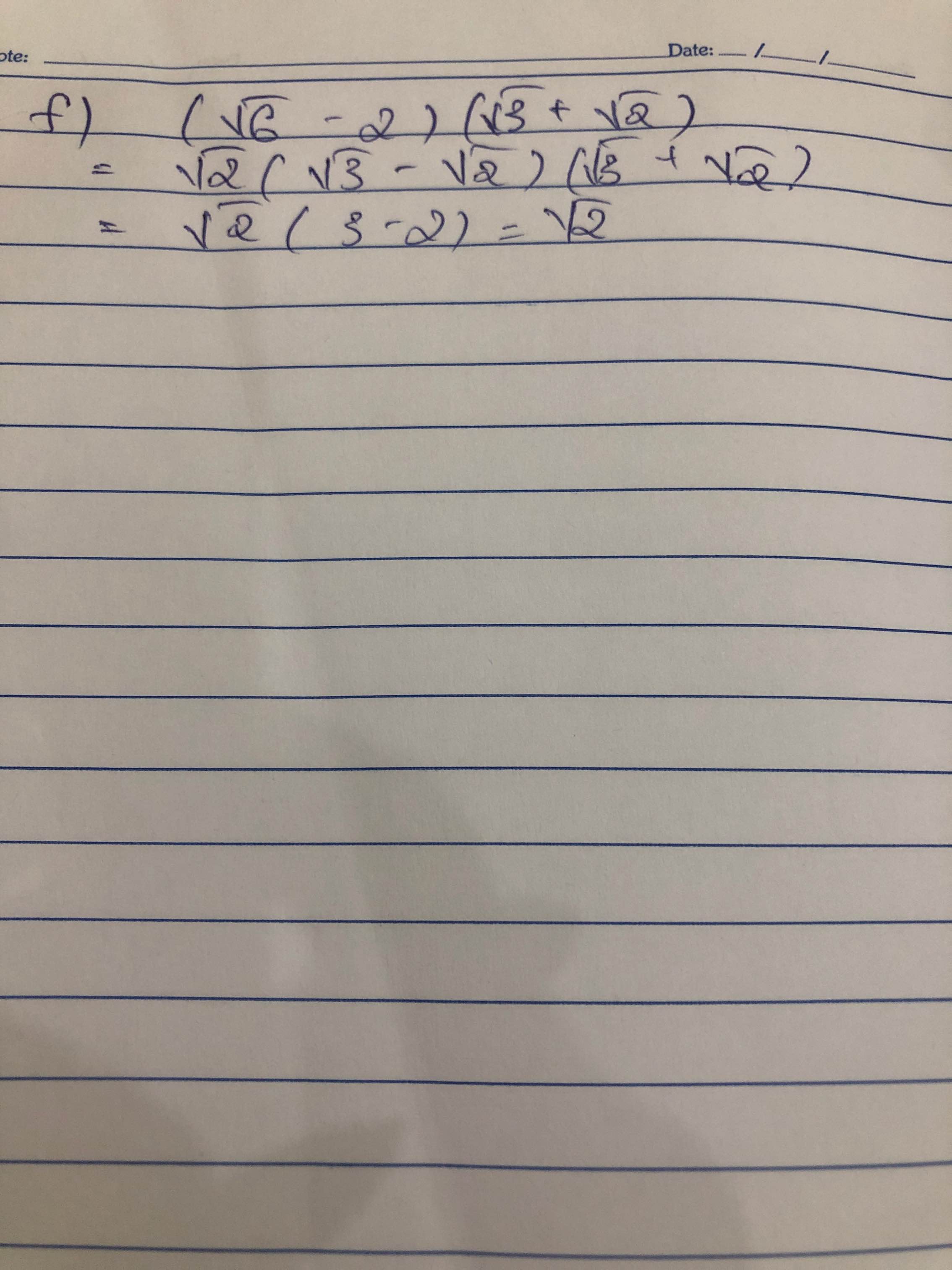\(2\sqrt{20}-\sqrt{50}+3\sqrt{80}-\sqrt{320}\)

\(=2.\sqrt{4}\sqrt{5}-\sqrt{25}\sqrt{2}+3.\sqrt{16}\sqrt{5}-\sqrt{64}\sqrt{5}\)

\(=2.2\sqrt{5}-5\sqrt{2}+3.4\sqrt{5}-8\sqrt{5}\)

\(=4\sqrt{5}-5\sqrt{2}+12\sqrt{5}-8\sqrt{5}=8\sqrt{5}-5\sqrt{2}\)

\(2\sqrt{20}-\sqrt{50}+3\sqrt{80}-\sqrt{320}=4\sqrt{5}-5\sqrt{2}+12\sqrt{5}-8\sqrt{5}=8\sqrt{5}-5\sqrt{2}\)

\(2\sqrt{20}-\sqrt{50}-3\sqrt{80}-\sqrt{320}=2\sqrt{2^2.5}-\sqrt{2.5^2}-3\sqrt{\left(2^2\right)^2.5}-\sqrt{\left(2^3\right)^2.5}=4\sqrt{5}-5\sqrt{2}-12\sqrt{5}-8\sqrt{5}=\left(4-12-8\right).\sqrt{5}-5\sqrt{2}=-16\sqrt{5}-5\sqrt{2}\)

\(1,4\sqrt{5}-5\sqrt{2}+12\sqrt{5}-8\sqrt{5}=8\sqrt{5}-5\sqrt{2}\)

\(2,\left(\sqrt{27}+\sqrt{32}-\sqrt{50}\right)\left(\sqrt{27}-\sqrt{32}+\sqrt{50}\right)\)

\(=27-\left(\sqrt{32}-\sqrt{50}\right)^2=27-2=25\)

a) \(2\sqrt{20}-\sqrt{50}+3\sqrt{80}-\sqrt{320}=2\sqrt{2^2.5}-\sqrt{5^2.2}+3\sqrt{4^2.5}-\sqrt{8^2.5}\\ =4\sqrt{5}-5\sqrt{2}+12\sqrt{5}-8\sqrt{5}=8\sqrt{5}-5\sqrt{2}\)

b) \(\sqrt{32}-\sqrt{50}+\sqrt{18}=\sqrt{4^2.2}-\sqrt{5^2.2}+\sqrt{3^2.2}=4\sqrt{2}-5\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)

c) \(3\sqrt{3}+4\sqrt{2}-5\sqrt{27}=3\sqrt{3}+4\sqrt{2}-5\sqrt{3^2.3}=3\sqrt{3}+4\sqrt{2}-15\sqrt{3}=4\sqrt{2}-12\sqrt{3}\)

d) \(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}+1}-1}-\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}+1}+1}=\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}+1}+1\right)-\sqrt{3}\left(\sqrt{\sqrt{3}+1}-1\right)}{\left(\sqrt{\sqrt{3}+1}-1\right)\left(\sqrt{\sqrt{3}+1}+1\right)}\\ =\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}+1}+1-\sqrt{\sqrt{3}+1}+1\right)}{\left(\sqrt{3+1}\right)^2-1^2}\\ =\dfrac{2\sqrt{3}}{\sqrt{3}}=2\)

e)\(\left(2+\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\right)\left(2-\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\right)=2^2-\left(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\right)^2=4-\left(\dfrac{9+6\sqrt{3}+3}{3+2\sqrt{3}+1}\right)\\ =4-\left(\dfrac{6\left(2+\sqrt{3}\right)}{2\left(2+\sqrt{3}\right)}\right)=4-3=1\)

b) \(\sqrt{32}-\sqrt{50}+\sqrt{18}=4\sqrt{2}-5\sqrt{2}+3\sqrt{2}=\left(4-5+3\right)\sqrt{2}=2\sqrt{2}\)

Tính hả bạn?

1,

\(2\sqrt{5}-\sqrt{125}-\sqrt{80}\\ =2\sqrt{5}-\sqrt{25\cdot5}-\sqrt{16\cdot5}\\ =2\sqrt{5}-5\sqrt{5}-4\sqrt{5}\\ =-7\sqrt{5}\)

2,

\(3\sqrt{2}-\sqrt{8}+\sqrt{50}-4\sqrt{32}\\ =3\sqrt{2}-\sqrt{4\cdot2}+\sqrt{25\cdot2}-4\sqrt{16\cdot2}\\ =3\sqrt{2}-2\sqrt{2}+5\sqrt{2}-16\sqrt{2}\\=-10\sqrt{2}\)

3,

\(\sqrt{18}-3\sqrt{80}-2\sqrt{50}+2\sqrt{45}\\ =\sqrt{9\cdot2}-3\sqrt{16\cdot5}-2\sqrt{25\cdot2}+2\sqrt{9\cdot5}\\ =3\sqrt{2}-12\sqrt{5}-10\sqrt{2}+6\sqrt{5}\\ =-7\sqrt{2}-6\sqrt{5}\)

4,

\(\sqrt{27}-2\sqrt{3}+2\sqrt{48}-3\sqrt{75}\\ =\sqrt{9\cdot3}-2\sqrt{3}+2\sqrt{16\cdot3}-3\sqrt{25\cdot2}\\ =3\sqrt{3}-2\sqrt{3}+8\sqrt{3}-15\sqrt{3}\\ =-6\sqrt{3}\)

5,

\(3\sqrt{2}-4\sqrt{18}+\sqrt{32}-\sqrt{50}\\ =3\sqrt{2}-4\sqrt{9\cdot2}+\sqrt{16\cdot2}-\sqrt{25\cdot2}\\ =3\sqrt{2}-12\sqrt{2}+4\sqrt{2}-5\sqrt{2}\\ =-10\sqrt{2}\)

6,

\(2\sqrt{3}-\sqrt{75}+2\sqrt{12}-\sqrt{147}\\ =2\sqrt{3}-\sqrt{25\cdot3}+2\sqrt{4\cdot3}-\sqrt{49\cdot3}\\ =2\sqrt{3}-5\sqrt{3}+4\sqrt{3}-7\sqrt{3}\\ =-6\sqrt{3}\)

7,

\(\sqrt{20}-2\sqrt{45}-3\sqrt{80}+\sqrt{125}\\ =\sqrt{4\cdot5}-2\sqrt{9\cdot5}-3\sqrt{16\cdot5}+\sqrt{25\cdot5}\\ =2\sqrt{5}-6\sqrt{5}-12\sqrt{5}+5\sqrt{5}\\ =-11\sqrt{5}\)

8,

\(6\sqrt{12}-\sqrt{20}-2\sqrt{27}+\sqrt{125}\\ =6\sqrt{4\cdot3}-\sqrt{4\cdot5}-2\sqrt{9\cdot3}+\sqrt{25\cdot5}\\ =12\sqrt{3}-2\sqrt{5}-6\sqrt{3}+5\sqrt{5}\\ =6\sqrt{3}+3\sqrt{5}\\ =3\left(2\sqrt{3}+\sqrt{5}\right)\)

9,

\(4\sqrt{24}-2\sqrt{54}+3\sqrt{6}-\sqrt{150}\\ =4\sqrt{4\cdot6}-2\sqrt{9\cdot6}+3\sqrt{6}-\sqrt{25\cdot6}\\ =8\sqrt{6}-6\sqrt{6}+3\sqrt{6}-5\sqrt{6}=0\)

10,

\(2\sqrt{18}-3\sqrt{80}-5\sqrt{147}+5\sqrt{245}-3\sqrt{98}\\ =2\sqrt{9\cdot2}-3\sqrt{16\cdot5}-5\sqrt{49\cdot3}+5\sqrt{49\cdot5}-3\sqrt{49\cdot2}\\ =6\sqrt{2}-12\sqrt{5}-35\sqrt{3}+35\sqrt{5}-21\sqrt{2}\\ =-15\sqrt{2}-35\sqrt{3}+23\sqrt{5}\)

a) Ta có: \(4\sqrt{28}+3\sqrt{63}-3\sqrt{112}-2\sqrt{175}\)

\(=8\sqrt{7}+9\sqrt{7}-12\sqrt{7}-10\sqrt{7}\)

\(=-5\sqrt{7}\)

b) Ta có: \(\sqrt{5}\left(\sqrt{5}-3\sqrt{20}+2\sqrt{80}\right)\)

\(=\sqrt{5}\left(\sqrt{5}-6\sqrt{5}+8\sqrt{5}\right)\)

\(=\sqrt{5}\cdot3\sqrt{5}=15\)

c) Ta có: \(\left(\sqrt{\dfrac{16}{3}}-\sqrt{\dfrac{25}{3}}\right)\cdot\sqrt{3}\)

\(=\dfrac{-1}{\sqrt{3}}\cdot\sqrt{3}\)

=-1

e) Ta có: \(\left(\sqrt{\dfrac{32}{3}}-\sqrt{54}+\sqrt{\dfrac{50}{3}}\right)\cdot\sqrt{6}\)

\(=\left(\dfrac{4\sqrt{2}}{\sqrt{3}}+\dfrac{5\sqrt{2}}{\sqrt{3}}-3\sqrt{6}\right)\cdot\sqrt{6}\)

\(=\dfrac{9\sqrt{12}}{\sqrt{3}}-18\)

\(=0\)

f) Ta có:  \(\left(\sqrt{6}-2\right)\left(\sqrt{3}+\sqrt{2}\right)\)

\(=3\sqrt{2}+2\sqrt{3}-2\sqrt{2}-2\sqrt{2}\)

\(=\sqrt{2}\)

1, \(\sqrt{8}-3\sqrt{32}+\sqrt{72}=2\sqrt{2}-12\sqrt{2}+6\sqrt{2}=-4\sqrt{2}\)

2,\(6\sqrt{12}-2\sqrt{48}+5\sqrt{75}-7\sqrt{108}=12\sqrt{3}-8\sqrt{3}+25\sqrt{3}-42\sqrt{3}=-13\sqrt{3}\)

3, \(\sqrt{20}+3\sqrt{45}-6\sqrt{80}-\dfrac{1}{3}\sqrt{125}=2\sqrt{5}+9\sqrt{5}-24\sqrt{5}-\dfrac{5}{3}.\sqrt{5}=-\dfrac{44}{3}.\sqrt{5}\)

4, \(2\sqrt{5}-\sqrt{125}-\sqrt{80}=2\sqrt{5}-5\sqrt{5}-4\sqrt{5}=-7\sqrt{5}\)

5, \(3\sqrt{2}-\sqrt{8}+\sqrt{50}-4\sqrt{32}=3\sqrt{2}-2\sqrt{2}+5\sqrt{2}-16\sqrt{2}=-10\sqrt{2}\)

Ối giời! Bấm máy tính đi bn! Người ta sinh ra cái máy tính là để làm mấy việc này mà. :D

\(1.\sqrt{12}-\sqrt{27}+\sqrt{3}\\ =2\sqrt{3}-3\sqrt{3}+\sqrt{3}\\ =0\)

\(2.\sqrt{252}-\sqrt{700}+\sqrt{1008}-\sqrt{448}\\ =6\sqrt{7}-10\sqrt{7}+12\sqrt{7}-8\sqrt{7}\\ =0\)

\(3\sqrt{112}-7\sqrt{216}+4\sqrt{54}-2\sqrt{252}-3\sqrt{96}\\ =12\sqrt{7}-42\sqrt{6}+12\sqrt{6}-12\sqrt{7}-12\sqrt{6}\\ =-42\sqrt{6}\)

\(4.\sqrt{18}-3\sqrt{80}-2\sqrt{50}+2\sqrt{45}\\ =3\sqrt{2}-12\sqrt{5}-10\sqrt{2}+6\sqrt{5}\\ =-7\sqrt{2}-6\sqrt{5}\)

\(5.6\sqrt{12}-\sqrt{20}-2\sqrt{27}+\sqrt{125}\\ =12\sqrt{3}-2\sqrt{5}-6\sqrt{3}+5\sqrt{5}\\ =6\sqrt{3}+3\sqrt{5}\)

\(6.2\sqrt{18}-3\sqrt{80}-5\sqrt{147}+5\sqrt{245}-3\sqrt{98}\\ =6\sqrt{2}-12\sqrt{5}-35\sqrt{3}+35\sqrt{5}-21\sqrt{2}\\ =-15\sqrt{2}-35\sqrt{3}+23\sqrt{5}\)