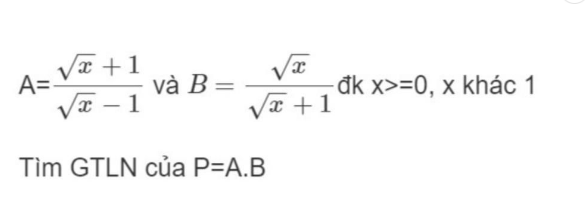
Đơn giản là em đang xem một lời giải sai. Việc khẳng định $P\leq 0$ hoặc $P>0$ rồi kết luận hàm số không có GTLN là sai.

Bởi vậy những câu hỏi ở dưới là vô nghĩa.

Việc gọi $P$ là hàm số lên lớp cao hơn em sẽ được học, còn bây giờ chỉ cần gọi đơn giản là phân thức/ biểu thức.

Hàm số, có dạng $y=f(x)$ biểu diễn mối liên hệ giữa biến $x$ với biến phụ thuộc $y$. Mỗi giá trị của $x$ ta luôn xác định được một giá trị tương ứng của $y$.

$P=AB=\frac{\sqrt{x}}{\sqrt{x}-1}=1+\frac{1}{\sqrt{x}-1}$

Để $P_{\max}$ thì $\frac{1}{\sqrt{x}-1}$ max

Điều này xảy ra khi $\sqrt{x}-1$ min và có giá trị dương 

$\Leftrightarrow x>1$ và $x$ nhỏ nhất

Trong tập số thực thì em không thể tìm được số lớn hơn 1 mà nhỏ nhất được. Như kiểu $1,00000000000000000000....$ (vô hạn đến không biết khi nào thì kết thúc)

Do đó $P$ không có max

Min cũng tương tự, $P$ không có min.

a) Tam thức \(f(x) = {x^2} - 1\) có \(\Delta  = 4 > 0\)nên f(x) có 2 nghiệm phân biệt \({x_1} =  - 1;{x_2} = 1\)

Mặt khác a=1>0, do đó ta có bảng xét dấu:

Tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)\)

b) Tam thức \(g(x) = {x^2} - 2x - 1\) có \(\Delta  = 8 > 0\) nên g(x) có 2 nghiệm phân biệt \({x_1} = 1 - \sqrt 2 ;{x_2} = 1 + \sqrt 2 \)

Mặt khác a = 1 > 0, do đó ta có bảng xét dấu:

Tập nghiệm của bất phương trình là \(\left( {1 - \sqrt 2 ;1 + \sqrt 2 } \right)\)

c) Tam thức \(h(x) =  - 3{x^2} + 12x + 1\) có\(\Delta ' = 39 > 0\)nên h(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - \sqrt {39} }}{3};{x_2} = \frac{{6 + \sqrt {39} }}{3}\)

Mặt khác a = -3 < 0, do đó ta có bảng xét dấu:

Tập nghiệm của bất phương trình là \(\left( { - \infty ; \frac{{6 - \sqrt {39} }}{3}} \right] \cup \left[ {\frac{{6 + \sqrt {39} }}{3}; + \infty } \right)\)

d) Tam thức \(k(x) = 5{x^2} + x + 1\) có \(\Delta  =  - 19 < 0\), hệ số a=5>0 nên k(x) luôn dương ( cùng dấu với a) với mọi x, tức là \(5{x^2} + x + 1 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm

các cạnh tương ứng tỉ lệ với nhau, mà ta tính các góc cũng dựa vào các tỉ lệ đó, nên 2 góc của tam giác đồng dạng bằng nhau 

ờ thì do 2x^2 =2x.2x- 1x cho nên có thừa số chung là x nên như v

có j thì bn kết bn với mình mình chỉ cho tk : ntd11223344

Thanks ạ !!

Sau giờ thứ nhất thì quãng đường còn lại là :

1 - \(\frac{2}{5}=\frac{3}{5}\)( quãng đường )

Giờ thứ hai bác Hùng đi được số phần quãng đường là :

             \(\frac{3}{5}\)x \(\frac{1}{2}\)= \(\frac{3}{10}\)( quãng đường )

Quãng đường còn lại sau giờ thứ nhất là

\(1-\frac{2}{5}=\frac{3}{5}\)( quãng đường )

Giờ thứ hai, Bác Hùng đi được số phần quãng đường là

\(\frac{3}{5}\times\frac{1}{2}=\frac{3}{10}\)( quãng đường )

Đáp số : \(\frac{3}{10}\)quãng đường

Ủng hộ tk Đúng nha mọi người ! ^^ 

C nha