cho a,b,c là các số thực
chứng minh rằng
a2+b2+c2+3\(\ge\)2(a+b+c)
Cho a,b,c là các số thực không âm thỏa mãn a2+b2+c2+abc=4 .Chứng minh rằng :
\(abc+2\ge ab+bc+ca\ge abc\)
Giả sử \(c\le1\).
Khi đó: \(ab+bc+ca-abc=ab\left(1-c\right)+c\left(a+b\right)\ge0\)
\(\Rightarrow ab+bc+ca\ge abc\left(1\right)\)
Đẳng thức xảy ra chẳng hạn với \(a=2,b=c=0\).
Theo giả thiết:
\(4=a^2+b^2+c^2+abc\ge2ab+c^2+abc\)
\(\Leftrightarrow ab\left(c+2\right)\le4-c^2\)
\(\Leftrightarrow ab\le2-c\)
Trong ba số \(\left(a-1\right),\left(b-1\right),\left(c-1\right)\) luôn có hai số cùng dấu.
Không mất tính tổng quát, giả sử \(\left(a-1\right)\left(b-1\right)\ge0\).
\(\Rightarrow ab-a-b+1\ge0\)
\(\Leftrightarrow ab\ge a+b-1\)
\(\Leftrightarrow abc\ge ca+bc-c\)
\(\Rightarrow abc+2\ge ca+bc+2-c\ge ab+bc+ca\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow\) Bất đẳng thức được chứng minh.
Cho a, b, c là các số thực dương thỏa mãn a+b+c=3 Chứng minh rằng: a2 +b2 + c2 +ab+bc+ca >= 6
Đặt \(P=a^2+b^2+c^2+ab+bc+ca\)
\(P=\dfrac{1}{2}\left(a+b+c\right)^2+\dfrac{1}{2}\left(a^2+b^2+c^2\right)\)
\(P\ge\dfrac{1}{2}\left(a+b+c\right)^2+\dfrac{1}{6}\left(a+b+c\right)^2=6\)
Dấu "=" xảy ra khi \(a=b=c=1\)
cho a, b, c là các số thực. Chứng minh rằng: a2 + b2 + c2 ≥ 2ab - 2bc +2ca
BĐT cần chứng minh tương đương:
\(a^2+b^2+c^2\ge2ab-2bc+2ca\)
\(\Leftrightarrow a^2+b^2+c^2+2bc-2a\left(b+c\right)\ge0\)
\(\Leftrightarrow a^2+\left(b+c\right)^2-2a\left(b+c\right)\ge0\)
\(\Leftrightarrow\left(a-b-c\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng
Cho các số thực dương a,b,c thỏa mãn a+b+c=3
Chứng minh rằng abc(1+a2)(1+b2)(1+c2)≤8
Cần gấp ko bạn
Nếu gấp thì sang web khác thử
Cho a ,b,c là các số thực không âm thỏa mãn a2+b2+c2=1.chứng minh rằng: c/1+bc + b/1+ca + a/1+bc >= 1
Cho a,b,c không âm. Chứng minh rằng :
a) a2 + b2 + c2 + 2abc + 2 > hoặc=ab +bc +ca +a+b+c
b)a2 + b2 +c2 +abc +4 > hoặc = 2(ab+bc+ca)
c) 3(a2 + b2 + c2) + abc +4 > hoặc =4 (ab+bc+ca)
d) 3(a2 + b2 + c2) + abc +80 > 4(ab+bc+ca) + 8(a+b+c)
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].
Câu 32. Tìm giá trị lớn nhất của biểu thức: ![]()
Câu 33. Tìm giá trị nhỏ nhất của: ![]() với x, y, z > 0.
với x, y, z > 0.
Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:
a) ab và a/b là số vô tỉ.
b) a + b và a/b là số hữu tỉ (a + b ≠ 0)
c) a + b, a2 và b2 là số hữu tỉ (a + b ≠ 0)
Câu 37. Cho a, b, c > 0. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 38. Cho a, b, c, d > 0. Chứng minh:
![]()
Câu 39. Chứng minh rằng [2x] bằng 2[x] hoặc 2[x] + 1
Câu 40. Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Câu 41. Tìm các giá trị của x để các biểu thức sau có nghĩa:
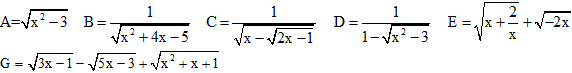 Mn giúp em với ;-;
Mn giúp em với ;-;
Cho các số thực không âm a,b,c thỏa mãn ab + bc + ca =1. Chứng minh rằng a2 +10(b2 + c2 ) ≥ 4
Lời giải:
Áp dụng BĐT Cô-si:
$\frac{a^2}{2}+8b^2\geq 2\sqrt{\frac{a^2}{2}.8b^2}=4ab$
$\frac{a^2}{2}+8c^2\geq 2\sqrt{\frac{a^2}{2}.8c^2}=4ac$
$2(b^2+c^2)\geq 2.2\sqrt{b^2c^2}=4bc$
Cộng các BĐT trên theo vế và thu gọn ta được:
$a^2+10(b^2+c^2)\geq 4(ab+bc+ac)=4$
Ta có đpcm.
Cho a, b, c là các số thực thỏa mãn ab+bc+ca=3. CMR:
(a2+2)(b2+2)(c2+2)-18 ≥ 3(a2+b2+c2)
Cho các số thực không âm a, b, c thỏa mãn a2 + b2 + c2 = 1. Chứng minh