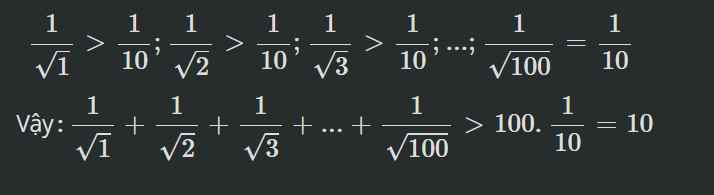Đặt \(A=1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2500}}\)

\(A=1+\frac{2}{2\sqrt{2}}+\frac{2}{2\sqrt{3}}+...+\frac{2}{2\sqrt{2500}}\)

\(A< 1+\frac{2}{\sqrt{1}+\sqrt{2}}+\frac{2}{\sqrt{2}+\sqrt{3}}+...+\frac{2}{\sqrt{2499}+\sqrt{2500}}\)

\(A< 1+2\left(\sqrt{2}-\sqrt{1}\right)+2\left(\sqrt{3}-\sqrt{2}\right)+...+2\left(\sqrt{2500}-\sqrt{2499}\right)\)

\(A< 1+2\left(\sqrt{2500}-1\right)=99< 100\)

Ta có :

\(\hept{\begin{cases}\frac{1}{2\sqrt{n+1}}< \frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{n+1-n}{\sqrt{n+1}+\sqrt{n}}\\\sqrt{n+1}-\sqrt{n}=\frac{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}{\sqrt{n+1}+\sqrt{n}}=\frac{n+1-n}{\sqrt{n+1}+\sqrt{n}}\end{cases}}\forall n\in N\)

Suy ra : \(\frac{1}{2\sqrt{n+1}}< \sqrt{n+1}-\sqrt{n}\)

Đặt \(M=1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2499}}+\frac{1}{\sqrt{2500}}\)

\(\Leftrightarrow\frac{1}{2}M=\frac{1}{2\sqrt{2500}}+\frac{1}{2\sqrt{2499}}+...+\frac{1}{2\sqrt{3}}+\frac{1}{2\sqrt{2}}+\frac{1}{2}\)

Áp dụng BĐT , ta có :

\(\frac{1}{2}M< \sqrt{2500}-\sqrt{2499}+\sqrt{2499}-\sqrt{2498}+...+\sqrt{3}-\sqrt{2}+\sqrt{2}-\sqrt{1}+\frac{1}{2}\)

\(\Rightarrow\frac{1}{2}M< \sqrt{2500}-\sqrt{1}+\frac{1}{2}=50-\frac{1}{2}< 50\)

\(\Rightarrow M< 100\)

`1)` Ta có `:` `1/sqrt1;1/sqrt2;1/sqrt3;…;1/sqrt99>1/sqrt100`

`=>` `1/sqrt1+1/sqrt2+1/sqrt3+…+1/sqrt99+1/sqrt100>100. 1/sqrt100=100/10=10`

`=>` `đpcm`

-Có: \(\dfrac{1}{\sqrt{1}}>\dfrac{1}{10};\dfrac{1}{\sqrt{2}}>\dfrac{1}{10};\dfrac{1}{\sqrt{3}}>\dfrac{1}{10};...;\dfrac{1}{\sqrt{99}}>\dfrac{1}{10}\)

\(\Rightarrow\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{99}}>\dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}\)

\(\Rightarrow\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{99}}+\dfrac{1}{10}>\dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}+\dfrac{1}{10}\)

\(\Rightarrow\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{99}}+\dfrac{1}{\sqrt{100}}>\dfrac{100}{10}=10\)

ai giúp mình với @@

\(\frac{1}{\sqrt{n}}=\frac{2}{2\sqrt{n}}>\frac{2}{\sqrt{n}+\sqrt{n+1}}=2\left(\sqrt{n+1}-\sqrt{n}\right)\)

Áp dụng BĐT ta có :

\(A=1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+....+\frac{1}{\sqrt{2500}}=2\left(\sqrt{2501}-\sqrt{2500}+\sqrt{2500}-\sqrt{2499}+....+\sqrt{2}-\sqrt{1}\right)\)

                                                                       \(=2\left(\sqrt{2501}-1\right)>2\left(\sqrt{2500}-1\right)=2.49=98\) (1)

\(\frac{1}{\sqrt{n}}=\frac{2}{2\sqrt{n}}<\frac{2}{\sqrt{n}+\sqrt{n-1}}=2\left(\sqrt{n}-\sqrt{n-1}\right)\)

ÁP dụng BĐT ta có :

\(A-1<2\left(\sqrt{2500}-\sqrt{2499}+...+\sqrt{3}-\sqrt{2}+\sqrt{2}-1\right)=2\left(\sqrt{2500}-1\right)=98\)

=> A  < 98 + 1 =99  (2)

Từ (1) và (2) => 98 < A < 99 

=> A không thể là số tự nhiên 

\(A<2\left(\sqrt{2500}-\sqrt{2499}+...+\sqrt{3}-\sqrt{2}+\sqrt{2}-\sqrt{1}+\sqrt{1}-0\right)\)

Vì 

\(\frac{1}{\sqrt{2}};\frac{1}{\sqrt{3}};\frac{1}{\sqrt{4}}....\) đều là số vô tỉ

Mà 1 là số hữu tỉ

=>\(A=1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}\) là một số vô tỉ 

Hay A ko phải là 1 số tự nhiên

Tick cho mình nha bạn.Nhân dịp năm mới chúc bạn mạnh khoẻ,vui vẻ,học giỏi nha.

Còn nhớ tui là ai nữa ko bạn???