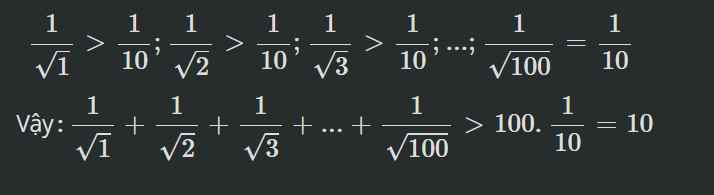`1)` Ta có `:` `1/sqrt1;1/sqrt2;1/sqrt3;…;1/sqrt99>1/sqrt100`
`=>` `1/sqrt1+1/sqrt2+1/sqrt3+…+1/sqrt99+1/sqrt100>100. 1/sqrt100=100/10=10`
`=>` `đpcm`
-Có: \(\dfrac{1}{\sqrt{1}}>\dfrac{1}{10};\dfrac{1}{\sqrt{2}}>\dfrac{1}{10};\dfrac{1}{\sqrt{3}}>\dfrac{1}{10};...;\dfrac{1}{\sqrt{99}}>\dfrac{1}{10}\)
\(\Rightarrow\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{99}}>\dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}\)
\(\Rightarrow\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{99}}+\dfrac{1}{10}>\dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}+\dfrac{1}{10}\)
\(\Rightarrow\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{99}}+\dfrac{1}{\sqrt{100}}>\dfrac{100}{10}=10\)