Lời giải:

1.

\(M(x)=A(x)-2B(x)+C(x)\)

\(2x^5 – 4x^3 + x^2 – 2x + 2-2(x^5 – 2x^4 + x^2 – 5x + 3)+ (x^4 + 4x^3 + 3x^2 – 8x + \frac{43}{16})\)

\(=5x^4+2x^2-\frac{21}{16}\)

2.

Khi $x=-\sqrt{0,25}=-0,5$ thì:

\(M(x)=5.(-0,5)^4+2(-0,5)^2-\frac{21}{16}=\frac{-1}{2}\)

3)

$M(x)=0$

$\Leftrightarrow 5x^4+2x^2-\frac{21}{16}=0$

$\Leftrightarrow 80x^4+32x^2-21=0$

$\Leftrightarrow 4x^2(20x^2-7)+3(20x^2-7)=0$

$\Leftrightarrow (4x^2+3)(20x^2-7)=0$

Vì $4x^2+3>0$ với mọi $x$ thực nên $20x^2-7=0$

$\Rightarrow x=\pm \sqrt{\frac{7}{20}}$

Đây chính là giá trị của $x$ để $M(x)=0$

0,2:x=1,03+3,97

a: A=-2xy+xy+xy^2=-xy+xy^2

Bậc là 3

b: \(B=xy^2z+2xy^2z-3xy^2z+xy^2z-xyz=-xyz+xy^2z\)

Bậc là 4

c: \(C=4x^2y^3-x^2y^3+x^4+6x^4-2x^2=3x^2y^3+7x^4-2x^2\)

Bậc là 5

d: \(D=\dfrac{3}{4}xy^2-\dfrac{1}{2}xy^2+xy=\dfrac{1}{4}xy^2+xy\)

bậc là 3

e: \(E=2x^2-4x^2+3z^4-z^4-3y^3+2y^3\)

=-2x^2+2z^4-y^3

Bậc là 4

f: \(=3xy^2z+xy^2z+2xy^2z-4xyz=6xy^2z-4xyz\)

Bậc là 4

Thay x = 1 vào pt ta được:

\(2.1^3+1^2-4.1-2\)

\(=2.1+1-4-2\)

\(=-3\)

Thay x = \(\dfrac{-1}{3}\) ta được:

\(2.\left(\dfrac{-1}{3}\right)^3+\left(\dfrac{-1}{3}\right)^2-4.\dfrac{-1}{3}-2\)

= \(2.\dfrac{-1}{27}+\dfrac{1}{9}+\dfrac{4}{3}-2\)

= \(\dfrac{-17}{27}\)

A= 2.x³+ x² -4x -2

- Với x=1, thay vào đa thức ta được:

A =\(2.1^3+1^2-4.1-2\)

= 2+1-4-2

= -3

Vậy giá trị của đa thức A tại x=1 là -3

- Với x \(=\dfrac{-1}{3}\) ,thay vào đa thức ta được:

A = \(2.\left(\dfrac{-1}{3}\right)^3+\left(\dfrac{-1}{3}\right)^2-4.\left(\dfrac{-1}{3}\right)-2\)

=\(2.\left(\dfrac{-1}{27}\right)+\dfrac{1}{9}+\dfrac{4}{3}-2\)

\(=\dfrac{-2}{27}+\dfrac{1}{9}+\dfrac{4}{3}-2\)

= \(\dfrac{-17}{27}\)

Vậy giá trị của đa thức A tại x=\(\dfrac{-1}{3}\) là \(\dfrac{-17}{27}\)

Ta có \(A\left(x\right)=\dfrac{1}{3}x+1=0\Leftrightarrow x=-1:\dfrac{1}{3}=-3\)

\(B\left(x\right)=-\dfrac{3}{4}x+\dfrac{1}{3}\Leftrightarrow x=-\dfrac{1}{3}\left(-\dfrac{3}{4}\right)=4\)

\(C=\left(2x-4\right)\left(x+1\right)=0\Leftrightarrow x=2;x=-1\)

\(D\left(x\right)-4x\left(x-2\right)=0\Leftrightarrow x=0;x=2\)

Tổng các hệ số của đa thức \(A\left(x\right)\) bất kì bằng giá trị của đa thức đó tại \(x=1\).

Thay \(x=1\) vào đa thức \(A\left(x\right)\) ta có:

\(A\left(1\right)=\left(3-4+1\right)^{2004}.\left(3+4+1\right)^{2005}=0\)

\(a.x^3+8-x^3+2=10\)

\(b.x^2+10x+25-4x\left(4x^2+12x+9\right)-\left(2x-1\right)\left(x^2-9\right)=x^2+10x+25-16x^3-28x^2-36x-2x^3+18x+x^2-9=-18x^3-26x^2-8x+16=\)

a) (x+2)²+x(x-4)

   =x²+4x+4+x²-4x

   =2x²+4

b)(x-3)²-(x+3)(x-4)

  =x²-6x+9-x²+4x-3x+12

  =-5x+12

c) (3x+1)²+3x(2-4x)

   =9x²+6x+1+6x-12x²

   =-3x²+12x+1

d) (2x-4y)²-(2x-3)(2x-3y)

  =4x²-16xy+16y²-4x²+6xy+6x-9y

  =16y²-10xy+6x-9y

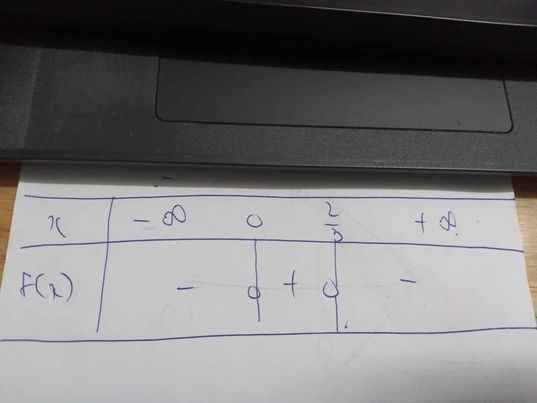
a: Đặt f(x)=0

=>\(-3x^2+2x=0\)

=>\(3x^2-2x=0\)

=>x(3x-2)=0

=>\(\left[{}\begin{matrix}x=0\\3x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)

Bảng xét dấu:

b: Đặt G(x)=0

=>\(x^2-10x+25=0\)

=>\(\left(x-5\right)^2=0\)

=>x-5=0

=>x=5

Bảng xét dấu:

c: Đặt H(x)=0

=>\(4x^2-4x+1=0\)

=>\(\left(2x-1\right)^2=0\)

=>2x-1=0

=>x=1/2

Bảng xét dấu:

d: Đặt Q(x)=0

=>(2x+3)(x-5)=0

=>\(\left[{}\begin{matrix}2x+3=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=5\end{matrix}\right.\)

Bảng xét dấu: