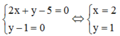x2+xy+y2=2x+y
x2+xy+y2=x+y
x2-3xy+3y2=3y
x2-2xy+5y2=1+y
Tìm x,y nguyên (giải theo lớp 7 nhé)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
phân tích đa thức sau thành nhân tử
x2 - 4x + 4 - y2
x2 + 2xy + y2 - x- y
x2 - 2xy + y2 - 9
2x3y + 2xy3 + 4x2y2 - 2xy
x2+y2-2xy + 4x - 4y
x3 - x + 3x2y + 3xy2 + y3 -y
x2 - 2xy +y2 - 4z2
x2 - x - y2 - y
x2 - 2xy + y2 - z2
`x^2 -4x+4-y^2`
`=(x^2 -4x+4)-y^2`
`=(x-2)^2 -y^2`
`=(x-2-y)(x-2+y)`
`x^2+2xy+y^2-x-y`
`=(x^2+2xy+y^2) -(x+y)`
`=(x+y)^2 -(x+y)`
`=(x+y)(x+y-1)`
`x^2-2xy+y^2-9`
`=(x^2-2xy+y^2)-3^2`
`=(x-y)^2-3^3`
`=(x-y-3)(x-y+3)`
Tách ra đi cậu.
1.
a.(-xy)(-2x2y+3xy-7x)
b.(1/6x2y2)(-0,3x2y-0,4xy+1)
c.(x+y)(x2+2xy+y2)
d.(x-y)(x2-2xy+y2)
2.
a.(x-y)(x2+xy+y2)
b.(x+y)(x2-xy+y2)
c.(4x-1)(6y+1)-3x(8y+4/3)
1.
\(a,\left(-xy\right)\left(-2x^2y+3xy-7x\right)\)
\(=2x^3y^2-3x^2y^2+7x^2y\)
\(b,\left(\dfrac{1}{6}x^2y^2\right)\left(-0,3x^2y-0,4xy+1\right)\)
\(=-\dfrac{1}{20}x^4y^3-\dfrac{1}{15}x^3y^3+\dfrac{1}{6}x^2y^2\)
\(c,\left(x+y\right)\left(x^2+2xy+y^2\right)\)
\(=\left(x+y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3\)
\(d,\left(x-y\right)\left(x^2-2xy+y^2\right)\)
\(=\left(x-y\right)^3\)
\(=x^3-3x^2y+3xy^2-y^3\)
2.
\(a,\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3-y^3\)
\(b,\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3+y^3\)
\(c,\left(4x-1\right)\left(6y+1\right)-3x\left(8y+\dfrac{4}{3}\right)\)
\(=24xy+4x-6y-1-24xy-4x\)
\(=\left(24xy-24xy\right)+\left(4x-4x\right)-6y-1\)
\(=-6y-1\)
#Toru
Tìm cặp số nguyên x ,y
x2 -2xy+ 5y2 = y-1
\(\Leftrightarrow x^2-2xy+5y^2-y+1=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(4y^2-y+\dfrac{1}{16}\right)+\dfrac{15}{16}=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(2y-\dfrac{1}{4}\right)^2+\dfrac{15}{16}=0\) (vô nghiệm)
Ko tồn tại x; y thỏa mãn pt
Tìm xy thõa mãn:
x2+3y2-4x+6y+7=0
3x2+y2+10x-2xy+26=0
3x2+6x2-12x-20y+40=0
Cho xy thõa mãn 2(x2+y2)=(x+y)2.Chứng minh rằng x=-y
\(x^2+3y^2-4x+6y+7=0\\ \Leftrightarrow\left(x^2-4x+4\right)+\left(3y^2+6y+3\right)=0\\ \Leftrightarrow\left(x-2\right)^2+3\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x-2=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)
\(3x^2+y^2+10x-2xy+26=0\\ \Leftrightarrow\left(x^2-2xy+y^2\right)+\left(2x^2+10x+\dfrac{25}{8}\right)+\dfrac{183}{8}=0\\ \Leftrightarrow\left(x-y\right)^2+2\left(x^2+2\cdot\dfrac{5}{2}x+\dfrac{25}{4}\right)+\dfrac{183}{8}=0\\ \Leftrightarrow\left(x-y\right)^2+2\left(x+\dfrac{5}{2}\right)^2+\dfrac{183}{8}=0\\ \Leftrightarrow x,y\in\varnothing\)
Sửa đề: \(3x^2+6y^2-12x-20y+40=0\)
\(\Leftrightarrow\left(3x^2-12x+12\right)+\left(6y^2-20y+\dfrac{50}{3}\right)+\dfrac{34}{3}=0\\ \Leftrightarrow3\left(x-2\right)^2+6\left(y^2-2\cdot\dfrac{5}{3}y+\dfrac{25}{9}\right)+\dfrac{34}{3}=0\\ \Leftrightarrow3\left(x-2\right)^2+6\left(y-\dfrac{5}{3}\right)^2+\dfrac{34}{3}=0\\ \Leftrightarrow x,y\in\varnothing\)
\(2\left(x^2+y^2\right)=\left(x+y\right)^2\\ \Leftrightarrow2x^2+2y^2=x^2+2xy+y^2\\ \Leftrightarrow x^2-2xy+y^2=0\\ \Leftrightarrow\left(x-y\right)^2=0\Leftrightarrow x-y=0\Leftrightarrow x=y\)
Tìm xy thõa mãn:
x2+3y2-4x+6y+7=0
3x2+y2+10x-2xy+26=0
3x2+6x2-12x-20y+40=0
Cho xy thõa mãn 2(x2+y2)=(x+y)2.Chứng minh rằng x=-y
phân tích đa thức thành nhân tử
x2-x-y2-y
x2-xy+x-y
x2-x-y2-y=(x2-y2)-(x+y)=(x-y)(x+y)-(x+y)=(x+y)(x-y-1)
x2-xy+x-y=x(x-y)+(x-y)=(x+1)(x-y)
6xy*(xy-y2)-8x2(x-y2)+5y2(x2+xy)voi x=1/2 y=2
\(6xy\left(xy-y^2\right)-8x^2\left(x-y^2\right)+5y^2\left(x^2+xy\right)\\ =6x^2y^2-6xy^3-8x^3+8x^2y^2+5x^2y^2+5xy^3\\ =\left(6x^2y^2+8x^2y^2+5x^2y^2\right)+\left(-6xy^3+5xy^3\right)-8x^3\\ =19x^2y^2-xy^3-8x^3\)
Với `x=1/2;y=2` ta có :
\(19x^2y^2-xy^3-8x^3\\ =19.\left(\dfrac{1}{2}\right)^2.2^2-\dfrac{1}{2}.2^3-8.2^3\\ =19.\dfrac{1}{4}.4-\dfrac{1}{2}.8-8.8\\ =19-4-64\\ =-49\)
Cho x,y là hai số thực dương thay đổi thỏa mãn điều kiện ( x y + 1 ) ( x y + 1 - y ) ≤ 1 - x - 1 y . Tìm giá trị lớn nhất của biểu thức P = x + y x 2 - x y + 3 y 2 - x - 2 y 6 ( x + y )
A. 5 3 - 7 30
B. 7 30 - 5 3
C. 5 3 + 7 30
D. 5 + 7 30
Giải pt nghiệm nguyên:
1) 3(x2-xy+y2)=7(x+y)
2) 5(x2+xy+y2)=7(x+2y)
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x(x - 3) + y(y - 3) + xy. Tìm giá trị Pmax của biểu thức P = 3 x + 2 y + 1 x + y + 6
A. Pmax = 0
B. Pmax = 2
C. Pmax = 1
D. Pmax = 3
Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
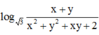
![]()
<=> ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
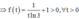
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
<=> ![]()
<=> ![]()
![]()
Khi đó, 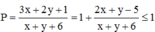
vì 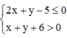
Vậy Pmax = 1 khi và chỉ khi