a,theo giả thiết E lần lượt là hình chiếu của H lên AB,

H là chân đường vuông góc kẻ từ B xuống AC

\(=>\)\(\angle\left(BEH\right)=\angle\left(BHA\right)=90^o\)

có \(\angle\left(B\right)chung\)\(=>\Delta BEH\sim\Delta BHA\left(g.g\right)\left(dpcm\right)\)

b, ta có E,F là hình chiếu của H trên AB,BC

\(=>HE\perp AB,HF\perp BC\)

mà \(BH\perp AC\left(gt\right)=>\)\(\Delta BHA\) vuông tại H có HE là đường cao

và \(\Delta BHC\) vuông tại H có HF là đường cao

theo hệ thức lượng

\(=>BH^2=BE.BA=BF.BC\left(dpcm\right)\)

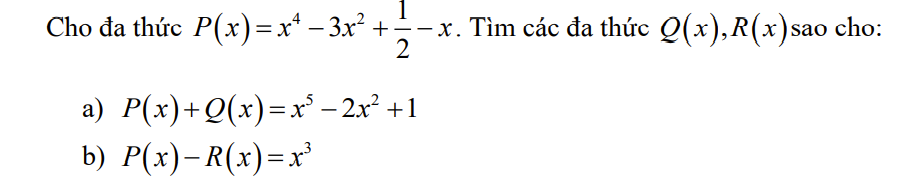
`a)P(x)+Q(x)=x^5-2x^2+1`

`=>Q(x)=x^5-2x^2+1-P(x)`

`=>Q(x)=x^5-2x^2+1-x^4+3x^2-1/2+x`

`=>Q(x)=x^5-x^4+x^2+x+1/2`

______________________________________________

`b)P(x)-R(x)=x^3`

`=>R(x)=P(x)-x^3`

`=>R(x)=x^4-3x^2+1/2-x-x^3`

`=>R(x)=x^4-x^3-3x^2-x+1/2`

Ta có:

\(P\left(x\right)+Q\left(x\right)=x^5-2x^2+1\)

\(\Rightarrow Q\left(x\right)=P\left(x\right)-\left(x^5-2x^2+1\right)\)

\(=x^4-3x^2+\dfrac{1}{2}-x-x^5+2x^2-1\)

\(=-x^5+x^4-x^2-x-\dfrac{1}{2}\)

Vậy \(Q\left(x\right)=-5^2+x^4-x^2-x-\dfrac{1}{2}\)

a) <=> Q(x) = (x⁵ - 2x² + 1) - P(x)

= (x⁵ - 2x² + 1) - (x⁴ - 3x² + 1/2 - x)

= x⁵ - 2x² + 1 - x⁴ + 3x² + x - 1/2

= x⁵ - x⁴ + x² + x + 1/2

Vậy Q(x) = x⁵ - x⁴ + x² + x + 1/2

Gọi \(\alpha\) là góc tạo với (d) và Ox

\(\Rightarrow tan\alpha=-1\)

\(\Rightarrow\alpha=135^0\)

Bài nào thế ạ

xét tg CHA và tg CAB

BCA chung

CHA=CAB=90

=>tg CHA đồng dạng CAB(gg)

=>CH/CA=CA/CB

=>CH.CB=CA²(1)

cm tương tự tg CKA đồng dạng tg CAD(gg)

=>CK/CA=CA/CD

=>CK.CD=CA²(2)

từ (1)(2)=>CH.CB=CK.CD

=>CH/CD=CK/CB

xét tg CKH và tg CBD

CH/CD=CK/CB

=>tg CKH đồng dạng tg CBD

\(H=\dfrac{Q_{thu}}{Q_{toa}}100\%=\dfrac{mc\Delta t}{Pt}100\%=\dfrac{10\cdot4200\cdot80}{1000\cdot1\cdot3600+10}100\%\approx93,1\%\)

\(A=Pt=1000\cdot\dfrac{7}{6}=\dfrac{3500}{3}\)Wh = \(\dfrac{7}{6}\)kWh

\(\Rightarrow T=A\cdot2100=\dfrac{7}{6}\cdot2100=2450\left(dong\right)\)

b, Ta có \(DE\cdot DF\cdot\cos E\cdot\cos F=DE\cdot DF\cdot\dfrac{DE}{EF}\cdot\dfrac{DF}{EF}=\dfrac{DE^2\cdot DF^2}{EF^2}\left(1\right)\)

Áp dụng HTL:\(DH\cdot EF=DE\cdot DF\Rightarrow DH=\dfrac{DE\cdot DF}{EF}\Rightarrow DH^2=\dfrac{DE^2\cdot DF^2}{EF^2}\left(2\right)\)

Từ (1)(2) ta được đpcm

b: DE//CF

=>sđ cung CD=sđ cung EF

góc AIB=1/2(sđ cung BD+sđ cung EF)

góc AOB=góc ACB=1/2*sđ cung BC

=1/2(sđ cung CD+sđcung DB)

=1/2(sđ cung EF+sđ cung DB)

=>góc AIB=góc AOB

=>AOIB nội tiếp

=>góc OIA=90 độ

=>I là trung điểm của DE