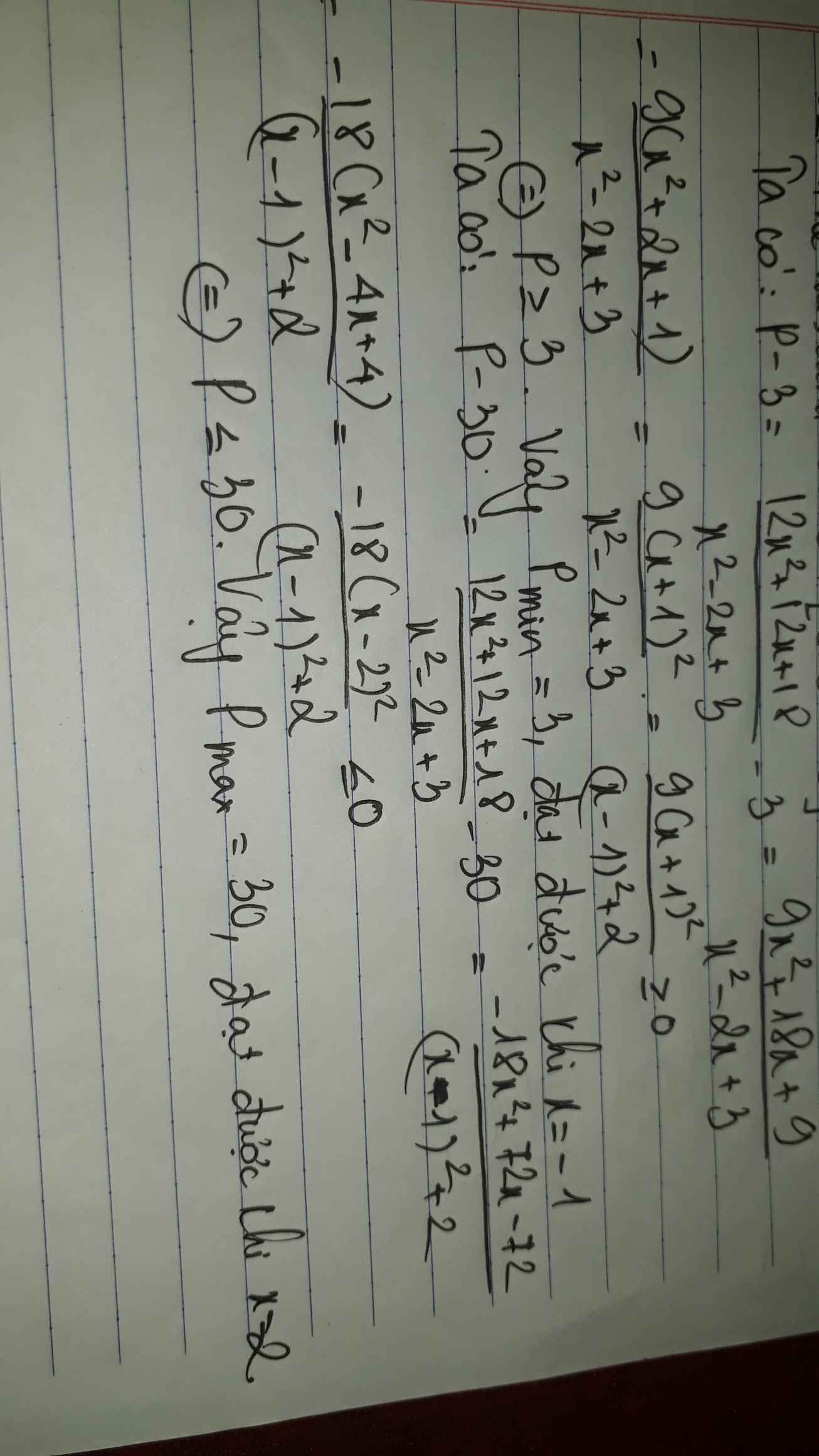\(P=\frac{12x^2-6x+4}{x^2+1}=\frac{\left(9x^2-6x+1\right)+3\left(x^2+1\right)}{x^2+1}=\frac{\left(3x-1\right)^2}{x^2+1}+3\ge3\forall x\)

Dấu "=" xảy ra khi: \(3x-1=0\Rightarrow x=\frac{1}{3}\)

Vậy \(P_{min}=3\Leftrightarrow x=\frac{1}{3}\)

Ta có :

\(P=\dfrac{12x^2-6x+4}{x^2+1}\)

\(=\dfrac{3x^2+3+9x^2-6x+1}{x^2+1}\)

\(=\dfrac{3\left(x^2+1\right)+\left(3x-1\right)^2}{x^2+1}\)

\(=3+\dfrac{\left(3x-1\right)^2}{x^2+1}\)

Do : \(\left\{{}\begin{matrix}\left(3x-1\right)^2\ge0\\x^2+1>0\end{matrix}\right.\Rightarrow3+\dfrac{\left(3x-1\right)^2}{x^2+1}\ge3\)

Vậy GTNN của P là 3 . Dấu \("="\) xảy ra khi \(\left(3x-1\right)^2=0\Leftrightarrow x=\dfrac{1}{3}\)

ta có gtnn của biểu thức là -3

tách ra hằng đẳng thức thứ...-2^3-2^3 -1 

= ( x+2 ) ^ 3 -9 còn lại tự nha

B=x+6x^2+12x+8-9

  =(x+2)^2-9

Vì(x+2)^2\(\ge\)0=>(x+2)^2-9\(\ge\)-9

Dấu = xảy ra <=>x+2=0

                     <=>x=-2

Vậy MinB=-9<=>x=-2

\(B=\dfrac{2x^2-12x+25}{x^2-6x+12}=\dfrac{2\left(x^2-6x+12\right)+1}{x^2-6x+12}=2+\dfrac{1}{x^2-6x+9+4}=2+\dfrac{1}{\left(x-3\right)^2+4}\le2+\dfrac{1}{4}=\dfrac{9}{4}\)

Không có min nha bạn . Chỉ có max thôi 

Dấu = xảy ra khi x=3

a: \(A=\dfrac{x^4+x^2+11x^2+11}{x^4+x^2+5x^2+5}=\dfrac{\left(x^2+11\right)\left(x^2+1\right)}{\left(x^2+5\right)\left(x^2+1\right)}=\dfrac{x^2+11}{x^2+5}\)

b: \(A=\dfrac{x^2+5+6}{x^2+5}=1+\dfrac{6}{x^2+5}< =1+\dfrac{6}{5}=\dfrac{11}{5}\)

Dấu = xảy ra khi x=0

a, \(A=-x^2-2x+3=-\left(x^2+2x-3\right)=-\left(x^2+2x+1-4\right)\)

\(=-\left(x+1\right)^2+4\le4\)

Dấu ''='' xảy ra khi x = -1 

Vậy GTLN là 4 khi x = -1 

b, \(B=-4x^2+4x-3=-\left(4x^2-4x+3\right)=-\left(4x^2-4x+1+2\right)\)

\(=-\left(2x-1\right)^2-2\le-2\)

Dấu ''='' xảy ra khi x = 1/2 

Vậy GTLN B là -2 khi x = 1/2 

c, \(C=-x^2+6x-15=-\left(x^2-2x+15\right)=-\left(x^2-2x+1+14\right)\)

\(=-\left(x-1\right)^2-14\le-14\)

Vâỵ GTLN C là -14 khi x = 1

Bài 8 : 

b, \(B=x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\)

Dấu ''='' xảy ra khi x = 3

Vậy GTNN B là 2 khi x = 3 

c, \(x^2-x+1=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)

Dấu ''='' xảy ra khi x = 1/2 

Vậy ...

c, \(x^2-12x+2=x^2-12x+36-34=\left(x-6\right)^2-34\ge-34\)

Dấu ''='' xảy ra khi x = 6

Vậy ...

\(A=\sqrt{1-6x+9x^2}+\sqrt{9x^2-12x+4}\)

\(A=\sqrt{1^2-2\cdot3x\cdot1+\left(3x\right)^2}+\sqrt{\left(3x\right)^2-2\cdot2\cdot3x+2^2}\)

\(A=\sqrt{\left(1-3x\right)^2}+\sqrt{\left(3x-2\right)^2}\)

\(A=\left|1-3x\right|+\left|3x-2\right|\)

\(A=\left|1-3x+3x-2\right|\)

\(A=\left|-1\right|=1\)

Dấu "=" xảy ra \(\left(1-3x\right)\left(3x-2\right)\ge0\)

\(\Rightarrow\dfrac{1}{3}\le x\le\dfrac{2}{3}\)

Vậy: \(A_{min}=1\) khi \(\dfrac{1}{3}\le x\le\dfrac{2}{3}\)