Hệ số góc của đường thẳng: y=-4x+9 là:
A. 4 B.-4x C.-4 D. 9
hệ số góc của đường thẳng y=-4x+9 làA4 B-4x C-4 D9
xác định hệ số góc của đường thẳng (d) 4x-5y=9
4x-5y=9
=>5y=4x-9
=>y=4/5x-9/5
=>Hệ số góc là 4/5
Câu 1: Giải phương trình và hệ phương trình
a) \(\sqrt{4x^2-4x+9}=3\)
b) \(\left\{{}\begin{matrix}3x-y=5\\2y-x=0\end{matrix}\right.\)
Câu 2:
a) Cho hai đường thẳng (d\(_1\)): y = 2x - 5 và (d\(_2\)): y = 4x - m (m là tham số). Tìm tất cả các giá trị của tham số m để (d\(_1\)) và (d\(_2\)) cắt nhau tại một điểm trên trục hoành Ox
b) Rút gọn biểu thức: \(P=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{2x}{9-x}\right):\left(\dfrac{\sqrt{x}-1}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\) với x > 0, x \(\ne\) 9, x \(\ne\) 25
a) \(\sqrt{4x^2-4x+9}=3\)
Vì \(4x^2-4x+9=\left(2x-1\right)^2+8>0\)( Với mọi x )
Nên \(\sqrt{4x^2-4x+9}=3\)
⇔\(4x^2-4x+9=9\)
⇔\(4x^2-4x=0\)
⇔\(4x\left(x-1\right)=0\)
⇔\(\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)là nghiệm
Câu 26. Cho hai đường tròn (C):(x-2)^ 2 +(y-2)^ 2 =9;(C' ):x^ 2 +y^ 2 +4x-8y+11=0 ,biết (C) và (C') đối xứng nhau qua đường thẳng (a) .Phương trình của (a) là : A. 2x + 2y - 4 = 0 B.2x-y+3=0 . C. x + y - 4 = 0 . D. 2x + 2y = 0 .
(Bài này làm như thế nào vậy ạ???)
Cho hai đường thẳng (d2): 4x+3y-23=0 và (d1): y=1, biết đường thẳng d là đường phân giác góc tù tạo bởi hai đường thẳng d1 và d2. Phương trình đường thẳng d là?
A. 2x-y+9=0
B. -2x-y+9=0
C. 2x+y+9=0
D. 2x-y-9=0
Viết phương trình đường thẳng (D) biết: 1. (D) có hệ số góc là 0,5 và qua B(2;-1) 2. (D)//(D*):y=5x − 3 và qua C (-2;4) 3, (D)// (D’):y= 4x – 3 và (D) cắt trục tung tại E có tung độ là 2 4. (D) qua G (2 ; −2) và (D) vuông góc (D’) : y= x+3 5. (D) vuông góc i (D): y = x + 3 và (D) đi qua giao điểm H của đường thẳng (D2): y = −x +4 với trục hoành 6. (D) qua gốc tọa độ và H (–2;1)
2: Vì (d)//(d') nên a=5
Vậy: (d): y=5x+b
Thay x=-2 và y=4 vào (d), ta được:
b-10=4
hay b=14
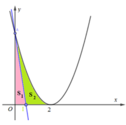
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - 4 x + 4 trục tung, trục hoành. Giá trị của k để đường thẳng d đi qua A(0;4) có hệ số góc k chia (H) thành 2 phần có diện tích bằng nhau là
A. K = -6
B. K = -2
C.K = -8
D. K = -4
Phương trình đường thẳng d đi qua A(0;4) có hệ số góc k

Vì d chia (H) thành 2 phần có diện tích bằng nhau
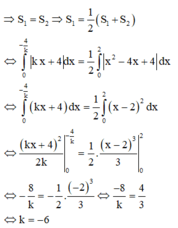
Đáp án A
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - 4 x + 4 trục tung, trục hoành. Giá trị của k để đường thẳng d đi qua A(0;4) có hệ số góc k chia (H) thành 2 phần có diện tích bằng nhau là
A. k = - 6
B. k = - 2
C. k = - 8
D. k = - 4
Đáp án A
Phương pháp: Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức : 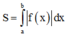
Cách giải: Phương trình đường thẳng d đi qua A(0;4) có hệ số góc k
![]()
Cho 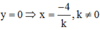 . Vậy, d cắt Ox tại điểm
. Vậy, d cắt Ox tại điểm 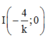
Giao điểm của y = x 2 - 4 x + 4 và trục hoành: Cho y = 0 => x = 2
=>Để d chia (H) thành 2 phần thì 
Vì d chia (H) thành 2 phần có diện tích bằng nhau
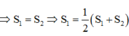
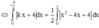
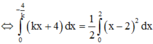
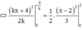
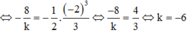
Biết rằng đồ thị hàm số y = ax cộng b vuông góc với đường thẳng y = -4x cộng 9 tìm a
Vì đồ thị hàm số y=ax+b vuông góc với y=-4x+9 nên ta có: -4a=-1
hay \(a=\dfrac{1}{4}\)