Sự biến thiên: Y=sinx Y=cosx Y=tanx Y=cotx

Những câu hỏi liên quan
tìm đạo hàm cấp n của hàm y=cosx; y=tanx; y=cotx; y=sinx.
\(y=sinx\Rightarrow y'=cosx;y''=-sinx;y'''=-cosx\)
Bằng quy nạp toán học ; ta c/m được : \(y^{\left(n\right)}sinx=sin\left(x+n\dfrac{\pi}{2}\right)\)
Đúng 2
Bình luận (0)
Cho biết chu kì của mỗi hàm số y = sin x , y = cos x , y = tan x , y = c o t x .
a. Hàm số y = sinx và y = cosx là hàm số tuần hoàn có chu kì là 2 π.
b. Hàm số y = tanx và y = cotx là các hàm số tuần hoàn có chu kì là π.
Đúng 0
Bình luận (0)
Hãy nêu tất cả các hàm số trong các hàm số
y
sin
x
,
y
cos
x
,
y
tan
x
,
y
c
o
t
x
thỏa mãn điều kiện đồng biến và nhận giá trị âm trong khoảng
-
π...
Đọc tiếp
Hãy nêu tất cả các hàm số trong các hàm số y = sin x , y = cos x , y = tan x , y = c o t x thỏa mãn điều kiện đồng biến và nhận giá trị âm trong khoảng - π 2 ; 0
A. y = tanx
B. y = sinx, y = cotx
C. y = sinx, y = tanx
D. y = tanx, y = cosx
Tìm tập xác đinh của các hàm số sau
29 , yfrac{tanx+cosx}{sinx}
30 , yfrac{1}{sinx}-frac{1}{cosx}
31 , yfrac{cosx+cotx}{sinx}
32 , yfrac{tanx+cotx}{1-sin2x}
33 , ytanx+frac{1}{cosfrac{x}{2}}
34 , yfrac{1-tanx}{1-cotx}
35 , yfrac{cotx}{cosx-1}
36 , yfrac{3}{sin^2x-cos^2x}
37 , yfrac{2}{cosx-cos3x}
38 , yfrac{sqrt{x}}{sinpi x}
39 , yfrac{2-cosx}{1+tanleft(x-frac{pi}{3}right)}
Đọc tiếp
Tìm tập xác đinh của các hàm số sau
29 , \(y=\frac{tanx+cosx}{sinx}\)
30 , \(y=\frac{1}{sinx}-\frac{1}{cosx}\)
31 , \(y=\frac{cosx+cotx}{sinx}\)
32 , \(y=\frac{tanx+cotx}{1-sin2x}\)
33 , \(y=tanx+\frac{1}{cos\frac{x}{2}}\)
34 , \(y=\frac{1-tanx}{1-cotx}\)
35 , \(y=\frac{cotx}{cosx-1}\)
36 , \(y=\frac{3}{sin^2x-cos^2x}\)
37 , \(y=\frac{2}{cosx-cos3x}\)
38 , \(y=\frac{\sqrt{x}}{sin\pi x}\)
39 , \(y=\frac{2-cosx}{1+tan\left(x-\frac{\pi}{3}\right)}\)
ĐKXĐ:
29.
\(\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow sinx.cosx\ne0\)
\(\Leftrightarrow sin2x\ne0\Leftrightarrow x\ne\frac{k\pi}{2}\)
30.
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow x\ne\frac{k\pi}{2}\) (như câu trên)
31.
\(sinx\ne0\Leftrightarrow x\ne k\pi\)
32.
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\sin2x\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\sin2x\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{2}\\x\ne\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
33.
\(\left\{{}\begin{matrix}cosx\ne0\\cos\frac{x}{2}\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{\pi}{2}+k\pi\\x\ne\pi+k2\pi\end{matrix}\right.\)
34.
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\cotx\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\cotx\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{2}\\x\ne\frac{\pi}{4}+k\pi\end{matrix}\right.\)
35.
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sinx\ne0\)
\(\Leftrightarrow x\ne k\pi\)
Đúng 0
Bình luận (0)
36.
\(sin^2x-cos^2x\ne0\Leftrightarrow cos2x\ne0\)
\(\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
37.
\(cos3x\ne cosx\Leftrightarrow\left\{{}\begin{matrix}3x\ne x+k2\pi\\3x\ne-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\frac{k\pi}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ne\frac{k\pi}{2}\)
38.
\(\left\{{}\begin{matrix}x\ge0\\sin\pi x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\pi x\ne k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne k\end{matrix}\right.\)
39.
\(\left\{{}\begin{matrix}cos\left(x-\frac{\pi}{3}\right)\ne0\\tan\left(x-\frac{\pi}{3}\right)\ne-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x-\frac{\pi}{3}\ne\frac{\pi}{2}+k\pi\\x-\frac{\pi}{3}\ne-\frac{\pi}{4}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{5\pi}{6}+k\pi\\x\ne-\frac{\pi}{12}+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Hàm số nào sau đây đồng biến trên khoản ( π/2 ; 3π/2 )
y=sinx y=cosx y=cotx y=tanxLời giải:
1. $y'=(\sin x)'=\cos x<0$ với mọi $x\in (\frac{\pi}{2}; \frac{3\pi}{2})$ nên hàm nghịch biến trên khoảng đã cho
2. $y'=-\sin x<0$ với mọi $x\in (\frac{\pi}{2}; \pi)$ nên hàm không đồng biến trên khoảng đã cho
3. \(y'=\frac{-1}{\sin ^2x}< 0, \forall x\in (\frac{\pi}{2}; \pi)\cup (\pi; \frac{3\pi}{2})\) nên loại
4. \(y'=\frac{1}{\cos ^2x}>0, \forall x\in (\frac{\pi}{2}; \frac{3\pi}{2})\) nên hàm đồng biến trên khoảng đã cho
Đáp án 4.
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
y
sin
x
+
cos
x
+
tan
x
+
c
o
t
x
+
1...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = sin x + cos x + tan x + c o t x + 1 sin x + 1 cos x
A. 2 2 - 1
B. 2 + 1
C. 2 2 + 1
D. 2 - 1
Đáp án A
Phương pháp: Đặt sinx = a, cosx = b
Cách giải: Đặt sinx = a, cosx = b ta có a2 + b2 = 1
Khi đó 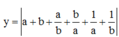
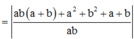
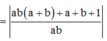
Đặt 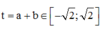
![]()
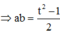
khi đó ta có : 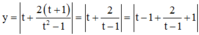
Nếu 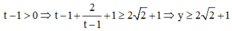
Nếu ![]()
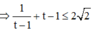
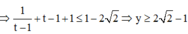
Vậy ![]()
Dấu bằng xảy ra ![]()
![]()
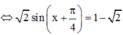
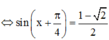
Đúng 0
Bình luận (0)
1. cho 180 độ x 250 độ. kết quả đúng làA. sinx0, cosx0B. sinx0, cosx0C. sinx0, cosx0D. sinx0, cosx02. cho dfrac{3pi}{4} x dfrac{3pi}{2} kết quả đúng làA. tanx0, cotx0B. tanx0, cotx0C. tanx0, cotx0D. tanx0, cotx03. cho 2pi x dfrac{5pi}{2} kết quả đúng làA. tanx0, cotx0B. tanx0, cotx0C. tanx0, cotx0D. tanx0, cotx04. cho 630 độ x 720 độ. kết quả đúng làA. sinx0, cosx0B. sinx0, cosx0C. sinx0, cosx0D. sinx0, cosx0
Đọc tiếp
1. cho 180 độ < x < 250 độ. kết quả đúng là
A. sinx>0, cosx>0
B. sinx<0, cosx<0
C. sinx>0, cosx<0
D. sinx<0, cosx>0
2. cho \(\dfrac{3\pi}{4}\) <x< \(\dfrac{3\pi}{2}\) kết quả đúng là
A. tanx>0, cotx>0
B. tanx<0, cotx<0
C. tanx>0, cotx<0
D. tanx<0, cotx>0
3.
cho 2\(\pi\) < x <\(\dfrac{5\pi}{2}\) kết quả đúng là
A. tanx>0, cotx>0
B. tanx<0, cotx<0
C. tanx>0, cotx<0
D. tanx<0, cotx>0
4.
cho 630 độ < x <720 độ. kết quả đúng là
A. sinx>0, cosx>0
B. sinx<0, cosx<0
C. sinx>0, cosx<0
D. sinx<0, cosx>0
Khẳng định nào sau đây là đúng?
A. Hàm số y = sinx là hàm số chẵn.
B. Hàm số y = cosx là hàm số chẵn
C. Hàm số y = tanx là hàm số chẵn
D. Hàm số y = cotx là hàm số chẵn
Ta có tập xác định của hàm số \(y=cosx\) là \(\mathbb{R}.\)
Nếu với \(x\in\mathbb{R}\) thì \(-x\in\mathbb{R}\) và\(y\left(-x\right)=cos\left(-x\right)=cosx=y\left(x\right).\)
Vậy hàm số \(y=cosx\) là hàm số chẵn.
\(\Rightarrow B\)
Đúng 2
Bình luận (0)
Xét sự biến thiên của hàm số y sinx - cosx. Tìm kết luận nào đúng? A. Hàm số đã cho đồng biến trên khoảng (
-
π
4
;
3
π
4
) B. Hàm số đã cho đồng biến trên khoảng (
3
π
4
;
7
π
4
) C. Hàm số đã...
Đọc tiếp
Xét sự biến thiên của hàm số y = sinx - cosx. Tìm kết luận nào đúng?
A. Hàm số đã cho đồng biến trên khoảng ( - π 4 ; 3 π 4 )
B. Hàm số đã cho đồng biến trên khoảng ( 3 π 4 ; 7 π 4 )
C. Hàm số đã cho có tập giá trị là [-1; 1]
D. Hàm số đã cho luôn nghịch biến trên khoảng ( - π 4 ; 7 π 4 )


















