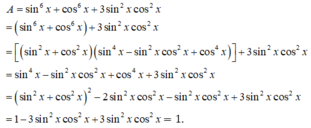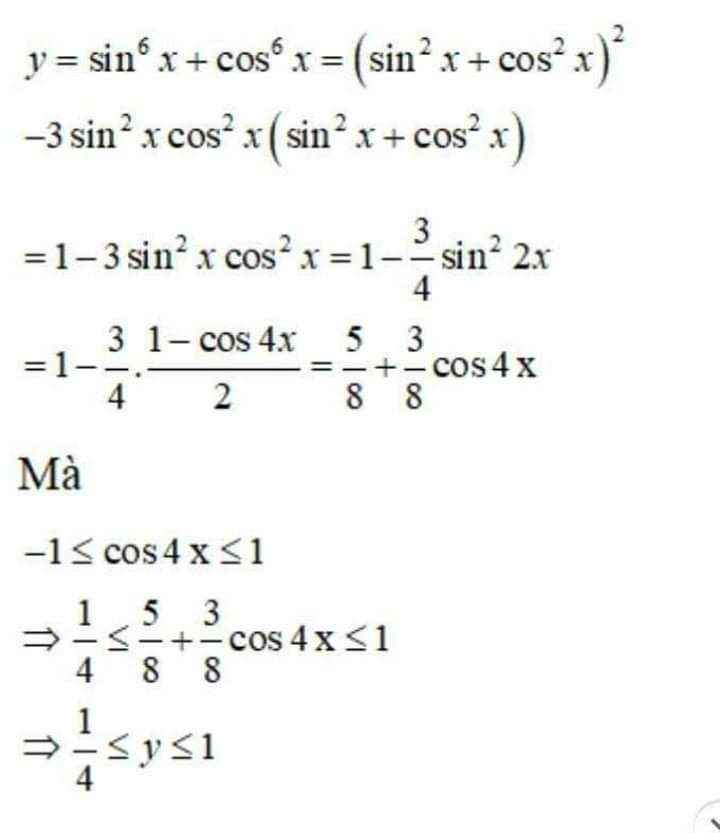sin6x + cos6x = 1 - \(\dfrac{3}{4}\)sin22x

Những câu hỏi liên quan
Rút gọn biểu thức : P=\(\dfrac{1+sin6x-cos6x}{1+sin6x+cos6x}\) sau đó tính P khi x= \(\dfrac{7\pi}{4}\)
\(P=\dfrac{1+2sin3xcos3x-\left(1-2sin^23x\right)}{1+2sin3xcos3x+2cos^2x-1}=\dfrac{2sin3xcos3x+2sin^23x}{2sin3xcos3x+2cos^23x}=\dfrac{sin3x}{cos3x}=tan3x\)
\(x=\dfrac{7\pi}{4}\Rightarrow P=tan\dfrac{21\pi}{4}=tan\dfrac{\pi}{4}=1\)
Đúng 0
Bình luận (0)
Tìm GTLN,GTNN của hàm số
y=4/3*(sin6x+cos6x)+cos4x-1
\(y=\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\)
\(\sin^6x+\cos^6x=\left(\sin^2x+\cos^2x\right)\left(\sin^4x-\sin^2x\cdot\cos^2x+\cos^4x\right)\\ =\left(\sin^2x+\cos^2x\right)^2-3\sin^2x\cdot\cos^2x=1-\dfrac{3}{4}\sin^22x\)
Do \(0\le\sin^22x\le1\Leftrightarrow\dfrac{3}{4}\cdot0\ge-\dfrac{3}{4}\sin^22x\ge-\dfrac{3}{4}\)
\(\Leftrightarrow1\ge1-\dfrac{3}{4}\sin^22x\ge1-\dfrac{3}{4}=\dfrac{1}{4}\\ \Leftrightarrow\dfrac{4}{3}\ge\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)\ge\dfrac{1}{4}\cdot\dfrac{4}{3}=\dfrac{1}{3}\)
Ta có \(-1\le\cos4x\le1\)
\(\Leftrightarrow\dfrac{1}{3}-1-1\le\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\le\dfrac{4}{3}+1-1\\ \Leftrightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
Vậy \(y_{min}=-\dfrac{5}{3};y_{max}=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
\(y=\dfrac{4}{3}\left(sin^6x+cos^6x\right)+cos4x-1\)
\(y=\dfrac{4}{3}\left(\dfrac{5}{8}+\dfrac{3}{8}cos4x\right)+cos4x-1\)
\(y=\dfrac{3}{2}cos4x-\dfrac{1}{6}\)
\(-1\le cos4x\le1\Rightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
\(y_{min}=-\dfrac{5}{3}\) khi \(cos4x=-1\)
\(y_{max}=\dfrac{4}{3}\) khi \(cos4x=1\)
Đúng 0
Bình luận (0)
Câu 1: Chứng minha) dfrac{cosx+sin2x}{1+sinx-cos2x}cotx b) dfrac{1+sin3x-cos6x}{cos3x+sin6x}tan3xCâu 2: Tínha) cos10.cos50.cos70b) sin10.sin50.sin70c) cos20.cos40.cos60.cos60d) sin20.sin40.sin60.sin80Câu 3: Trong mặt phẳng Oxy, cho tam giác ABC có điểm A(-4;2) và đường cao CH : x-y-10; trung điểm của BC là I(-2;3). Tìm tọa độ đỉnh BCâu 4: Trong mặt phẳng Oxy, cho tam giác ABC có điểm B(-1;2) và đường cao AH : x+y-20; trung điểm của AC là I(-2;1). Viết phương trình cạnh ACCâu 5: Cho các số dương...
Đọc tiếp
Câu 1: Chứng minh
a) \(\dfrac{cosx+sin2x}{1+sinx-cos2x}=cotx\)
b) \(\dfrac{1+sin3x-cos6x}{cos3x+sin6x}=tan3x\)
Câu 2: Tính
a) cos10.cos50.cos70
b) sin10.sin50.sin70
c) cos20.cos40.cos60.cos60
d) sin20.sin40.sin60.sin80
Câu 3: Trong mặt phẳng Oxy, cho tam giác ABC có điểm A(-4;2) và đường cao CH : x-y-1=0; trung điểm của BC là I(-2;3). Tìm tọa độ đỉnh B
Câu 4: Trong mặt phẳng Oxy, cho tam giác ABC có điểm B(-1;2) và đường cao AH : x+y-2=0; trung điểm của AC là I(-2;1). Viết phương trình cạnh AC
Câu 5: Cho các số dương x,y thỏa mãn x+ y = \(\dfrac{1}{2}\). Tìm giá trị nhỏ nhất của
P=\(\dfrac{1}{x}+\dfrac{1}{y}\)
Câu 6: Cho số thực x thỏa mãn x>4. Tìm giá trị nhỏ nhất của \(Q=9x+\dfrac{1}{x-4}\)
Câu 7: Cho số dương x thỏa mãn 0 ≤ x ≤ 7. Tìm giá trị lớn nhất của \(Q=9x\left(7-x\right)\)
Câu 8: Trong mặt phẳng Oxy cho đường tròn (C): x2 + y2 - 2x + 2y - 7 = 0 và đường thẳng d: x + y + 1 = 0. Viết phương trình đường thẳng △ song song với đường thẳng d và cắt đường tròn (C) theo dây cung có độ dài bằng 2.
Câu 9: Trong mặt phẳng Oxy cho điểm A(-3;4) và đường thẳng d: 3x + 4y + 18 = 0. Viết phương trình đường tròn tâm A và cắt đường thẳng d theo dây cung có độ dài bằng 24
Câu 10: Trong mặt phẳng Oxy cho đường tròn (C): x2 + y2 - 2x + 2y - 7 =0 và đường thẳng d: x + y + 1=0. Viết phương trình đường thẳng △ song song với đường thẳng d và cắt đường tròn (C) theo dây cung AB sao cho tam giác ABI đều (I là tâm của (C))
Giúp em với ạ <3 Được câu nào hay câu đó :( tsau em thi rùi
Câu 5. Cho x,y dương thỏa mãn \(x+y=\dfrac{1}{2}\).Tìm giá trị nhỏ nhất của
\(P=\dfrac{1}{x}+\dfrac{1}{y}\)
Giải:
\(P=\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{x+y}{xy}=\dfrac{\dfrac{1}{2}}{xy}=\dfrac{2}{xy}\)
--> P nhỏ nhất khi \(xy\) lớn nhất
Ta có:
\(x^2+y^2\ge2xy\) ( BĐT AM-GM )
\(\Leftrightarrow\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow1\ge4xy\)
\(\Leftrightarrow xy\le\dfrac{1}{4}\)
\(\Rightarrow P\ge2:\dfrac{1}{4}=8\)
Vậy \(Min_P=8\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{4}\)
Đúng 5
Bình luận (4)
1) Giai
a) cos6x + sin6x
Bài 3: Rút gọn biểu thức: a) A = sin6x + 3sin4x.cos2x + 3sin2x.cos4x + cos6x b) B = (1 + cosα)(1 – cosα) – sin2α
b: \(B=\left(1+\cos\alpha\right)\left(1-\cos\alpha\right)-\sin^2\alpha\)
\(=1-\cos^2\alpha-\sin^2\alpha\)
=0
Đúng 0
Bình luận (0)
Giá trị của biểu thức A = sin 6 x + cos 6 x + 3 sin 2 c o s 2 là :
A. A = -1
B. A = 1
C. A = 4
D. A = -4
Tìm điều kiện của m để phương trình:
sin
6
x
+
4
cos
6
x
m
có nghiệm.
Đọc tiếp
Tìm điều kiện của m để phương trình: sin 6 x + 4 cos 6 x = m có nghiệm.
![]()
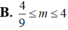
![]()
![]()
1) Gia tri lon nhat cua ham so: y = sin6x + cos6x
Trong khoảng
(
-
π
;
π
)
, phương trình
s
i
n
6
x
+
3
s
i
n
2
x
c
o
s
x
+
c
o
s
6
x
1
có A. 4 nghiệm B. 1 nghiệm C. 3 nghiệm D. 2 nghiệm
Đọc tiếp
Trong khoảng ( - π ; π ) , phương trình s i n 6 x + 3 s i n 2 x c o s x + c o s 6 x = 1 có
A. 4 nghiệm
B. 1 nghiệm
C. 3 nghiệm
D. 2 nghiệm
Biểu thức A = 3(sin4x + cos4x) - 2 (sin6x + cos6x) có giá trị bằng:
A. 1
B. 2
C. -1
D. 0
Chọn A.
Ta có:
+ sin4x + cos4x = (sin2x + cos2x)2 - 2sin2x.cos2x = 1 - 2sin2x.cos2x.
+ sin4x + cos4x = 1 - 3sin2x.cos2x.
Do đó
A = 3(1 - 2sin2x.cos2x) - 2(1 - 3sin2x.cos2x) = 1.
Đúng 0
Bình luận (0)