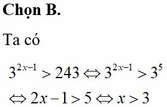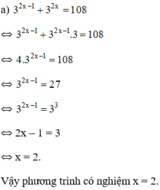32x + 1 = 243

Những câu hỏi liên quan
c) 23x + 2 = 4x + 5
d) 32x - 1 = 243
Tìm tập nghiệm S của bất phương trình
3
2
x
-
1
243
A.
S
-
∞
;
3
B.
S
3
:
+
∞
C.
S
2...
Đọc tiếp
Tìm tập nghiệm S của bất phương trình 3 2 x - 1 > 243
A. S = - ∞ ; 3
B. S = 3 : + ∞
C. S = 2 : + ∞
D. S = - ∞ ; 2
Tìm x,biết:
a)2x - 1 = 32
b)32x + 1 =81
c)2x - 26 = 6
d)27.3x=243
a: Ta có: \(2^{x-1}=32\)
\(\Leftrightarrow x-1=5\)
hay x=6
b: Ta có: \(3^{2x+1}=81\)
\(\Leftrightarrow2x+1=4\)
\(\Leftrightarrow2x=3\)
hay \(x=\dfrac{3}{2}\)
c: Ta có: \(2^x-26=6\)
\(\Leftrightarrow2^x=32\)
hay x=5
d: Ta có: \(27\cdot3^x=243\)
\(\Leftrightarrow3^x=9\)
hay x=2
Đúng 1
Bình luận (0)
Tìm x, biết rằng: a) 2x = 16 b) 3x+1 = 9xc) 23x+2 = 4x+5d) 32x-1 = 243
a) 2x = 16 <=>x=8
b) 3x+1 = 9x <=>9x-3x=1
<=>6x=1 <=>x=1/6
c) 23x+2 = 4x+5 <=>23x-4x=5-2
<=>19x=3 <=>x=3/19
d) 32x-1 = 243 <=>32x=244
<=>x=61/8
Đúng 0
Bình luận (0)
a/ 2x=16
x=8
b/ 3x+1=9x
3x-9x=-1
-6x=-1
x=1/6
c/ 23x+2=4x
23x-4x=-2
19x=-2
x=-2/19
d/ 32x-1=243
32x=244
x=61/8
Đúng 0
Bình luận (0)
Tìm \(x,y\in N\):
a) 32x+1 . 7y = 9 . 21x
b) \(\dfrac{27^x}{3^{2x-y}}=243\) và \(\dfrac{25^x}{5^{x+y}}=125\)
Lời giải:
a)
$3^{2x+1}.7^y=9.21^x=3^2.(3.7)^x=3^{2+x}.7^x$
Vì $x,y$ là số tự nhiên nên suy ra $2x+1=2+x$ và $y=x$
$\Rightarrow x=y=1$
b) \(\frac{27^x}{3^{2x-y}}=\frac{3^{3x}}{3^{2x-y}}=3^{x+y}=243=3^5\Rightarrow x+y=5(1)\)
\(\frac{25^x}{5^{x+y}}=\frac{5^{2x}}{5^{x+y}}=5^{x-y}=125=5^3\Rightarrow x-y=3\) $(2)$
Từ $(1);(2)\Rightarrow x=4; y=1$
Đúng 1
Bình luận (0)
Bài 1 : Tìm x, biết : a. 2x 16 b. 3x+1 9x c. 23x+2 4x+5 d. 32x-1 243 Bài 2 : So sánh : a. 2225 và 3150 b. 291 và 535 c. 9920 và 999910 Bài 3 : Chứng minh các đẳng thức : a. 128 . 912 1816 b. 7520 4510 . 530 .
Đọc tiếp
Bài 1 : Tìm x, biết :
a. 2x = 16 b. 3x+1 = 9x
c. 23x+2 = 4x+5 d. 32x-1 = 243
Bài 2 : So sánh :
a. 2225 và 3150 b. 291 và 535 c. 9920 và 999910
Bài 3 : Chứng minh các đẳng thức :
a. 128 . 912 = 1816 b. 7520 = 4510 . 530 .
\(1,\\ a,2^x=16=2^4\Rightarrow x=4\\ b,3^{x+1}=9^x=3^{2x}\\ \Rightarrow x+1=2x\Rightarrow x=1\\ c,2^{3x+2}=4^{x+5}=2^{2\left(x+5\right)}\\ \Rightarrow3x+2=2x+10\Rightarrow x=8\\ d,3^{2x-1}=243=3^5\\ \Rightarrow2x-1=5\Rightarrow x=3\\ 2,\\ a,2^{225}=8^{75}< 9^{75}=3^{150}\\ b,2^{91}=\left(2^{13}\right)^7=8192^7>3125^7=\left(5^5\right)^7=5^{35}\\ c,99^{20}=\left(99^2\right)^{10}< \left(99\cdot101\right)^{10}=9999^{10}\\ 3,\\ a,12^8\cdot9^{12}=2^{16}\cdot3^8\cdot3^{24}=2^{16}\cdot3^{32}=\left(2\cdot3^2\right)^{16}=18^{16}\\ b,75^{20}=\left(3\cdot5^2\right)^{20}=3^{20}\cdot5^{40}=\left(3^{20}\cdot5^{10}\right)\cdot5^{30}=\left(3^2\cdot5\right)^{10}\cdot5^{30}=45^{10}\cdot5^{30}\)
Đúng 2
Bình luận (0)
Bài 1:
a) \(\Rightarrow2^x=2^4\Rightarrow x=4\)
b) \(\Rightarrow3^{x+1}=3^{2x}\Rightarrow x+1=2x\Rightarrow x=1\)
c) \(\Rightarrow2^{3x+2}=2^{2x+10}\Rightarrow3x+2=2x+10\Rightarrow x=8\)
d) \(\Rightarrow3^{2x-1}=3^5\Rightarrow2x-1=5\Rightarrow x=3\)
Bài 2:
a) \(2^{225}=\left(2^3\right)^{75}=8^{75}< 9^{75}=\left(3^2\right)^{75}=3^{150}\)
b) \(2^{91}=\left(2^{13}\right)^7=8192^7>3125^7=\left(5^5\right)^7=5^{35}\)
c) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\)
Bài 3:
a) \(12^8.9^{12}=\left(4.3\right)^8.9^{12}=4^8.3^8.9^{12}=2^{16}.9^4.9^{12}=2^{16}.9^{16}=\left(2.9\right)^{16}=18^{16}\)
b) \(75^{20}=\left(75^2\right)^{10}=5625^{10}=\left(45.125\right)^{10}=45^{10}.125^{10}=45^{10}.5^{30}\)
Đúng 2
Bình luận (0)
Giải các phương trình mũ: 3 2 x - 1 + 3 2 x = 108
Cộng các phân thức khác mẫu thức:
3
2
x
+
3
x
-
3
2
x
-
1
+
2
x
2
+
1
4
x
2
-
2
x
Đọc tiếp
Cộng các phân thức khác mẫu thức: 3 2 x + 3 x - 3 2 x - 1 + 2 x 2 + 1 4 x 2 - 2 x
Mẫu thức chung: 4 x 2 - 2 x = 2 x 2 x - 1
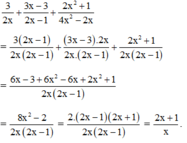
Đúng 0
Bình luận (0)
32x-1=27x+2
\(3^{2x-1}=27^{x+2}\)
\(\Leftrightarrow3x+6=2x-1\)
hay x=-7
Đúng 0
Bình luận (0)
32x-1=27x+2
Ta có: \(3^{2x-1}=27^{x+2}\)
\(\Leftrightarrow3x+6=2x-1\)
hay x=-7
Đúng 0
Bình luận (0)