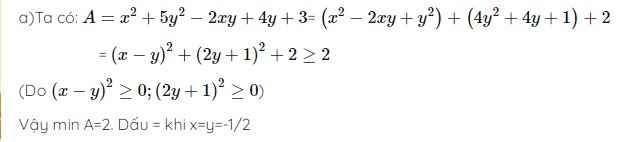Tìm GTLN: x2+5x+7. Tìm GTNN: 6x-x2-5. Giúp mình

Những câu hỏi liên quan
1.Tìm GTNN của Bthức : B= 4x2- 6x+1 : (x-2)2 với x ≠ 2
2. Tìm GTLN của Bthức: C= x2 + 4x - 14 : x2 -2x +1 với x≠ 1
giúp mình với ạ, mình cảm ơn nhiều ạ
1.
Đặt \(x-2=t\ne0\Rightarrow x=t+2\)
\(B=\dfrac{4\left(t+2\right)^2-6\left(t+2\right)+1}{t^2}=\dfrac{4t^2+10t+5}{t^2}=\dfrac{5}{t^2}+\dfrac{2}{t}+4=5\left(\dfrac{1}{t}+\dfrac{1}{5}\right)^2+\dfrac{19}{5}\ge\dfrac{19}{5}\)
\(B_{min}=\dfrac{19}{5}\) khi \(t=-5\) hay \(x=-3\)
2.
Đặt \(x-1=t\ne0\Rightarrow x=t+1\)
\(C=\dfrac{\left(t+1\right)^2+4\left(t+1\right)-14}{t^2}=\dfrac{t^2+6t-9}{t^2}=-\dfrac{9}{t^2}+\dfrac{6}{t}+1=-\left(\dfrac{3}{t}-1\right)^2+2\le2\)
\(C_{max}=2\) khi \(t=3\) hay \(x=4\)
Đúng 0
Bình luận (0)
a. tìm gtnn của
A= (x2-2x)2+10.(x2-2x)2+39
b. tìm gtln của
B=4x-2x2+1
nhanh giúp mình với ạ, mình đang gấp
b: Ta có: \(B=-2x^2+4x+1\)
\(=-2\left(x^2-2x-\dfrac{1}{2}\right)\)
\(=-2\left(x^2-2x+1-\dfrac{3}{2}\right)\)
\(=-2\left(x-1\right)^2+3\le3\forall x\)
Dấu '=' xảy ra khi x=1
Đúng 2
Bình luận (0)
Bài 6: a)Tìm GTLN, GTNN của biểu thức sau:a. x2 – 6x +11 b. –x2 + 6x – 11 c) Chứng minh rằng: x2 + 2x + 2 0 với x Z
Đọc tiếp
Bài 6: a)Tìm GTLN, GTNN của biểu thức sau:
a. x2 – 6x +11 b. –x2 + 6x – 11
c) Chứng minh rằng: x2 + 2x + 2 > 0 với x Z
c: \(=\left(x+1\right)^2+1>0\forall x\)
Đúng 0
Bình luận (0)
Trả lời:
a, \(x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTNN của biểu thức bằng 2 khi x = 3
b, \(-x^2+6x-11=-\left(x^2-6x+11\right)=-\left(x^2-6x+9+2\right)=-\left[\left(x-3\right)^2+2\right]\)
\(=-\left(x-3\right)^2-2\le-2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTLN của biểu thức bằng - 2 khi x = 3
c, \(x^2+2x+2=x^2+2x+1+1=\left(x+1\right)^2+1\ge1>0\forall x\inℤ\) (đpcm)
Dấu "=" xảy ra khi x + 1 = 0 <=> x = - 1
tìm GTNN của biểu thức :
B=2x2 40x-15
C=x2-4xy+5y2-4y+28
Tìm GTLN của biểu thức :
D= - x2+4x+3
E=x-x2
F=\(\dfrac{5}{x^{2+2x+5}}\)
Mọi người ơi, giúp mình bài này với, cảm ơn mọi người nhiều nha !!!
Tìm GTNN hoặc GTLN của các biểu thức sau:
a) 2x2 - x + 1
b) 5x - x2 + 4
c) x2 + 5y2 - 2xy + 4y + 3
a) \(2x^2-x+1=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)
\(ĐTXR\Leftrightarrow x=\dfrac{1}{4}\)
b) \(5x-x^2+4=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\)
\(ĐTXR\Leftrightarrow x=\dfrac{5}{2}\)
c) \(x^2+5y^2-2xy+4y+3=\left(x-y\right)^2+\left(2y+1\right)^2+2\ge2\)
\(ĐTXR\Leftrightarrow\)\(x=y=-\dfrac{1}{2}\)
Đúng 3
Bình luận (0)
b: ta có: \(-x^2+5x+4\)
\(=-\left(x^2-5x-4\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{41}{4}\right)\)
\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
Tìm GTLN của các biểu thức sau:
A = 6x - 3x2 - 7
B = 5x - 2x2 + 1
C = 2x2 - 8x + 13
D = x2 - 3x + 5
\(A=-3x^2+6x-7=-3\left(x^2-2x+1-1\right)-7\)
\(=-3\left(x-1\right)^2-4\le-4\)Dấu ''='' xảy ra khi x = 1
\(B=-2x^2+5x+1=-2\left(x^2-\dfrac{5}{2}x\right)+1\)
\(=-2\left(x^2-2.\dfrac{5}{4}x+\dfrac{25}{16}-\dfrac{25}{16}\right)+1\)
\(=-2\left(x-\dfrac{5}{4}\right)^2+\dfrac{33}{8}\le\dfrac{33}{8}\)Dấu ''='' xảy ra khi x = 5/4
C;D chỉ có GTNN thôi bạn nhé \(C=2x^2-8x+13=2\left(x^2-4x+4-4\right)+13\)
\(=2\left(x-2\right)^2+5\ge5\)Dấu ''='' xảy ra khi x = 2
\(D=x^2-3x+5=x^2-2.\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{9}{4}+5\)
\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\)Dấu ''='' xảy ra khi x = 3/2
Đúng 2
Bình luận (0)
d: Ta có: \(D=x^2-3x+5\)
\(=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{11}{4}\)
\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm GTNN hoặc GTLN của các biểu thức sau:
a) A = x2 + 3x + 4
b) B = 2x2 - x + 1
c) C = 5x - x2 + 4
d) D = x2 + 5y2 - 2xy + 4y + 3
a: Ta có: \(A=x^2+3x+4\)
\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\)
\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
tìm GTLN/GTNN: x2 - 4x +7
\(x^2-4x+7\)
⇔ \(\left(x^2-4x+4\right)+3\)
⇔ \(\left(x-2\right)^2+3\)
Vì \(\left(x-2\right)^2\ge0\) ⇒ \(\left(x-2\right)^2+3\ge3\)
Vậy GTNN của A là 3 khi x =2
Đúng 0
Bình luận (0)
\(x^2-4x+7\)
\(=x^2-4x+4+3\)
\(=\left(x-2\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 0
Bình luận (0)
Tìm GTLN hoặc GTNN của các đa thưc sau:
Xem chi tiết
a, -x2 + 2x + 3
b, x2 - 2x + 4y2 - 4y + 8 c, -x2 - y2 + xy + 2x + 2y + 4 d, x2 + 5y2 - 4xy - 2y + 2015 e, 2x2 + y2 + 6x + 2y + 2xy + 2018A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
Đúng 4
Bình luận (0)
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2
Đúng 2
Bình luận (0)
tìm gtnn (gtln) của
a) 4x2+12x+1 b) 4x2-3x+10
c)2x2+5x+10 d) x-x2+2
e) 2x-2x2 f) 4x2+2y2+4xy+4y+5
a) \(4x^2+12x+1=\left(4x^2+12x+9\right)-8=\left(2x+3\right)^2-8\ge-8\)
\(ĐTXR\Leftrightarrow x=-\dfrac{3}{2}\)
b) \(4x^2-3x+10=\left(4x^2-3x+\dfrac{9}{16}\right)+\dfrac{151}{16}=\left(2x-\dfrac{3}{4}\right)^2+\dfrac{151}{16}\ge\dfrac{151}{16}\)
\(ĐTXR\Leftrightarrow x=\dfrac{3}{8}\)
c) \(2x^2+5x+10=\left(2x^2+5x+\dfrac{25}{8}\right)+\dfrac{55}{8}=\left(\sqrt{2}x+\dfrac{5\sqrt{2}}{4}\right)^2+\dfrac{55}{8}\ge\dfrac{55}{8}\)
\(ĐTXR\Leftrightarrow x=-\dfrac{5}{4}\)
d) \(x-x^2+2=-\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{9}{4}=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}\le\dfrac{9}{4}\)
\(ĐTXR\Leftrightarrow x=\dfrac{1}{2}\)
e) \(2x-2x^2=-2\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{2}=-2\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{2}\le\dfrac{1}{2}\)
\(ĐTXR\Leftrightarrow x=\dfrac{1}{2}\)
f) \(4x^2+2y^2+4xy+4y+5=\left(4x^2+4xy+y^2\right)+\left(y^2+4y+4\right)+1=\left(2x+y\right)^2+\left(y+2\right)^2+1\ge1\)
\(ĐTXR\Leftrightarrow\) \(\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (1)
a: Ta có: \(4x^2+12x+1\)
\(=4x^2+12x+9-8\)
\(=\left(2x+3\right)^2-8\ge-8\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{3}{2}\)
b: Ta có: \(4x^2-3x+10\)
\(=4\left(x^2-\dfrac{3}{4}x+\dfrac{5}{2}\right)\)
\(=4\left(x^2-2\cdot x\cdot\dfrac{3}{8}+\dfrac{9}{64}+\dfrac{151}{64}\right)\)
\(=4\left(x-\dfrac{3}{8}\right)^2+\dfrac{151}{16}\ge\dfrac{151}{16}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{8}\)
c: Ta có: \(2x^2+5x+10\)
\(=2\left(x^2+\dfrac{5}{2}x+5\right)\)
\(=2\left(x^2+2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}+\dfrac{55}{16}\right)\)
\(=2\left(x+\dfrac{5}{4}\right)^2+\dfrac{55}{8}\ge\dfrac{55}{8}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{5}{4}\)
Đúng 3
Bình luận (1)