\(x^2+y^2-2x-2y+3\)

\(=x^2-2.x.1+1^2+y^2-2.y.1+1^2+1\)

\(=\left(x-1\right)^2+\left(y-1\right)^2+1>0+0+0=0\)

a) \(x^2+2xy+y^2+1\\ =\left(x+y\right)^2+1\\Do\left(x+y\right)^2>0\forall x\in R\\ \Rightarrow\left(x+y\right)^2+1>0\forall\in R\)

Đáp án A

Ta có, giả thiết  log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính  R 1 = 2

Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m  là đường tròn tâm I(-2;-3); R 2 = m  

Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9

Đáp án A

Ta có, giả thiết

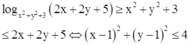
là miền trong đường tròn tâm I(1;1) bán kính R₁ = 2

Và 

\(Q=\dfrac{x+y}{2\left(x-y\right)}-\dfrac{x-y}{2\left(x+y\right)}+\dfrac{x^2+y^2}{\left(x-y\right)\left(x+y\right)}\)

\(=\dfrac{x^2+2xy+y^2-x^2+2xy-y^2+2x^2+2y^2}{2\left(x-y\right)\left(x+y\right)}\)

\(=\dfrac{2x^2+2y^2+4xy}{2\left(x-y\right)\left(x+y\right)}=\dfrac{2\left(x+y\right)^2}{2\left(x-y\right)\left(x+y\right)}=\dfrac{x+y}{x-y}\)

\(x^2-2xy+y^2+1=\left(x^2-2xy+y^2\right)+1=\left(x-y\right)^2+1>0\) nhé!

\(x-x^2-1=-\left(x^2-x+1\right)=-\left(x^2-2.x.\dfrac{1}{2}+\dfrac{1}{4}\right)-\dfrac{3}{4}=-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}< 0\)

x2 là x² hả bạn???

a: x>2

y>2

=>x+y>2+2=4

x>y>2

=>xy>2^2=4

b: x^2-xy=x(x-y)

x-y>0; x>0

=>x(x-y)>0

=>x^2-xy>0

y>2

=>y-2>0

=>y(y-2)>0

=>y^2-2y>0

x>y và y>2

=>y>0 và x-y>0

=>y(x-y)>0

=>xy-y^2>0