Dùng đồ thị (C) biện luận theo m số nghiệm của phương trình
(C): y= (x2+1)/(x2)
(m-1)x2+2x-1=0
Những câu hỏi liên quan
a) Khảo sát hàm số y x3 + 3x2 + 1 (1)
b) Dựa vào đồ thị (C) của hàm số (1), biện luận về số nghiệm của phương trình
x2 (x + 3) m theo m
Đọc tiếp
a) Khảo sát hàm số y= x3 + 3x2 + 1 (1)
b) Dựa vào đồ thị (C) của hàm số (1), biện luận về số nghiệm của phương trình
x2 (x + 3) = m theo m
9B. Cho parabol (P) : y = 1/2 x^2
a) Vẽ (P) trên mặt phẳng tọa độ.
b) Dựa vào đồ thị hãy biện luận theo m số nghiệm của phương trình x2
– 2m + 4=0
giúp tui làm câu b ạ
a: 
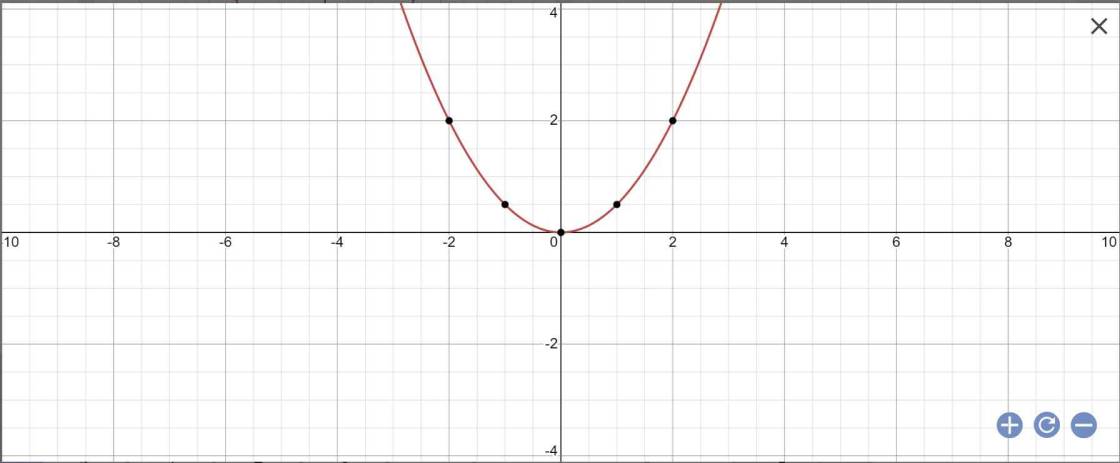
b: \(\Delta=\left(-2m\right)^2-4\cdot1\cdot4=4m^2-16\)
Để phương trình có hai nghiệm phân biệt thì 4m^2-16>0
=>m>2 hoặc m<-2
Để phương trình có nghiệm duy nhất thì 4m^2-16=0
=>m=2 hoặc m=-2
Để phương trìh vô nghiệm thì 4m^2-16<0
=>-2<m<2
Đúng 1
Bình luận (0)
Cho đồ thị hàm số y = x\(^2\) -2x - 3 :
Dựa vào đồ thị biện luận theo m số nghiệm của phương trình: x^2 - 2x - 3 + m = 0
Cho phương trình (lần x) x²-2(m-2) x+m² =0 (1) (m là tham số) 1: tìm m để phương trình (1) có nghiệm 2: Trong trường hợp phương trình (1) có nghiệm. Gọi x1, x2 là hai nghiệm của phương trình (1) a: dùng định lí Vi-Ét hãy tính x1+x2 và x1.x2 theo m b: tìm m để x1.x2-(x1+x2)-2=0
Cho phương trình (m+2)x2−2(m−1)x+3−m=0 (1); với m là tham số thực
1) Giải và biện luận phương trình đã cho theo tham số m
2) Tìm m để phương (1) có hai nghiệm thỏa mãn tổng hai nghiệm bằng tích hai nghiệm.
1: Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot\left(m+2\right)\left(3-m\right)\)
\(=\left(2m-2\right)^2+4\left(m+2\right)\left(m-3\right)\)
\(=4m^2-8m+4+4\left(m^2-3m+2m-6\right)\)
\(=4m^2-8m+4+4m^2-4m-24\)
\(=-12m-20\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow-12m-20>0\)
\(\Leftrightarrow-12m>20\)
hay \(m< \dfrac{-5}{3}\)
Để phương trình có nghiệm kép thì Δ=0
\(\Leftrightarrow-12m-20=0\)
\(\Leftrightarrow-12m=20\)
hay \(m=\dfrac{-5}{3}\)
Để phương trình vô nghiệm thì Δ<0
\(\Leftrightarrow-12m-20< 0\)
\(\Leftrightarrow-12m< 20\)
hay \(m>\dfrac{-5}{3}\)
Đúng 0
Bình luận (1)
2: ĐKXĐ: \(m\ne-2\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m+2}=\dfrac{2m-2}{m+2}\\x_1\cdot x_2=\dfrac{3-m}{m+2}\end{matrix}\right.\)
Ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow\dfrac{2m-2}{m+2}=\dfrac{3-m}{m+2}\)
Suy ra: 2m-2=3-m
\(\Leftrightarrow2m+m=3+2\)
\(\Leftrightarrow3m=5\)
hay \(m=\dfrac{5}{3}\)(thỏa ĐK)
Đúng 0
Bình luận (0)
Câu 2:1) Cho hàm số ydfrac{1}{4}x^2 có đồ thị (P). Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy2) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 25Câu 3:1) Tìm giá trị của tham số m để phương trình x2 - 2x + m 0 có hai nghiệm phân biệt2) Cho x1 và x2 là hai nghiệm của phương trình x2 - 2x - 1 03) Tính giá trị của biểu thức T (x1)2 + (x2)2
Đọc tiếp
Câu 2:
1) Cho hàm số \(y=\dfrac{1}{4}x^2\) có đồ thị (P). Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy
2) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 25
Câu 3:
1) Tìm giá trị của tham số m để phương trình x2 - 2x + m = 0 có hai nghiệm phân biệt
2) Cho x1 và x2 là hai nghiệm của phương trình x2 - 2x - 1 = 0
3) Tính giá trị của biểu thức T = (x1)2 + (x2)2
Câu 2:1) Cho hàm số ydfrac{1}{4}x^2 có đồ thị (P). Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy2) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 25Câu 3:1) Tìm giá trị của tham số m để phương trình x2 - 2x + m 0 có hai nghiệm phân biệt2) Cho x1 và x2 là hai nghiệm của phương trình x2 - 2x - 1 03) Tính giá trị của biểu thức T (x1)2 + (x2)2
Đọc tiếp
Câu 2:
1) Cho hàm số \(y=\dfrac{1}{4}x^2\) có đồ thị (P). Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy
2) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 25
Câu 3:
1) Tìm giá trị của tham số m để phương trình x2 - 2x + m = 0 có hai nghiệm phân biệt
2) Cho x1 và x2 là hai nghiệm của phương trình x2 - 2x - 1 = 0
3) Tính giá trị của biểu thức T = (x1)2 + (x2)2
(P): y= (1 - m)x2 - mx - 3
a) tìm m để hàm số đạt GTLN
b) Vẽ (P) ứng mới m= -1
c) Dùng đồ thị để biện luận theo k số nghiệm của phương trình : x2 - 1/2x -k = 0
d) Dùng đồ thị để biện luận theo k số nghiệm của phương trình : | 2x2 + x - 3 | = k
C1 : Điểm M (2;4) thuộc đồ thị của hàm số nàoA. y -x2 B. y x2 C. y -2x2 D. y 2x2C2 : Gọi x1; x2 là hai nghiệm của pt x2 + x - 1 0. Khi đó biểu thức x12 + x22 có giá trị làA. 1 B. 3 C. -1 D. -3C3. Gọi x1; x2 là hai nghiệm của pt x2 + 2 (m - 1) x + m2 0. Khi đó tổng và tích hai nghiệm theo m làA. x1 + x2 -2 (m - 1) / x1 . x2 m2B. x1 + x2 2 (m - 1) / x1 . x2 -m2C. x1 + x2 2 (m -1) / x1 . x2 m2D. x1 + x2 -2 (m -1) / x1 . x2 -m2C4....
Đọc tiếp
C1 : Điểm M (2;4) thuộc đồ thị của hàm số nào
A. y= -x2 B. y= x2 C. y= -2x2 D. y= 2x2
C2 : Gọi x1; x2 là hai nghiệm của pt x2 + x - 1 = 0. Khi đó biểu thức
x12 + x22 có giá trị là
A. 1 B. 3 C. -1 D. -3
C3. Gọi x1; x2 là hai nghiệm của pt x2 + 2 (m - 1) x + m2 = 0. Khi đó tổng và tích hai nghiệm theo m là
A. x1 + x2 = -2 (m - 1) / x1 . x2 = m2
B. x1 + x2 = 2 (m - 1) / x1 . x2 = -m2
C. x1 + x2 = 2 (m -1) / x1 . x2 = m2
D. x1 + x2 = -2 (m -1) / x1 . x2 = -m2
C4. Cho pt x2 - (a + 1) x + a = 0. Khi đó phương trình có 2 nghiệm là
A. x1 = 1 ; x2 = -a B. x1 = -1 ; x2 = -a
C. x1 = -1 ; x2 = a D. x1 = 1 ; x2 = a
( 2 điểm )
1) Cho phương trình x2- 2x + m = 0 ( với m là số thực thoả mãn m < 1 ). Chứng minh phương trình đã cho có hai nghiệm phân biệt.
2) Cho x1 và x2 là hai nghiệm của phương trình x2+ 2x- 1 = 0.
Tính giá trị của biểu thức P = \(\dfrac{1}{x_1}\)+ \(\dfrac{1}{x_2}\)
1) \(\Delta'=1-m>0\forall m< 1\)
Vậy phương trình đã cho luôn có hai nghiệm phân biệt
2) Do a = 1; c = -1 nên a và c trái dấu
Do đó phương trình luôn có hai nghiệm phân biệt
Theo Viét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-1\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_2+x_1}{x_1x_2}=\dfrac{-2}{-1}=2\)
Đúng 3
Bình luận (0)