Cho \(y=\left(m+1\right)x+3m-2\). Tìm điểm mà đồ thị đi qua với mọi giá trị của m

Những câu hỏi liên quan
Cho hàm số \(y=\left(2m+2\right)x+m-1.\). Tìm điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị của m.
Cho hàm số y (m-1)x + m +3 1) Tìm giá trị của m để đồ thị của hàm số song song với đồ thị hàm số y -2x + 1. 2) Tim giá trị của m để đồ thị của hàm số đi qua điểm (1; -4). 3) Tìm điểm cố định mà đồ thị của hàm số luôn đi qua với mọi m. 4) Tim giá trị của m để đồ thị của hàm số tạo với trục tung và trục hoành một tam giác có diện tích bằng 1 (đvdt).
Đọc tiếp
Cho hàm số y= (m-1)x + m +3
1) Tìm giá trị của m để đồ thị của hàm số song song với đồ thị hàm số y= -2x + 1.
2) Tim giá trị của m để đồ thị của hàm số đi qua điểm (1; -4).
3) Tìm điểm cố định mà đồ thị của hàm số luôn đi qua với mọi m.
4) Tim giá trị của m để đồ thị của hàm số tạo với trục tung và trục hoành một tam giác có diện tích bằng 1 (đvdt).
Vì hs y = (m-1)x +m +3 đi qua điểm (1; -4) nên ta đc :
-4 = (m-1) + m+3
<=> -4 = 2m + 2
<=> m =-3
Đúng 1
Bình luận (0)
1) Đặt tên cho dễ giải nè:
(d1) : y= (m-1) x + m+ 3
(d2) : y = -2x + 1
(d1) // (d2) <=> m - 1 = -2 và m+ 3 \(\ne\)1
<=> m = -1 và m \(\ne\)-2
Đúng 0
Bình luận (0)
1. để đồ thị của hàm số \(y=\left(m-1\right)x+m+3\) // với \(y=-2x+1\),
\(\left\{{}\begin{matrix}m-1=-2\\m+3\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m\ne-2\end{matrix}\right.\)
2. để đi qua điểm (1;-4),
\(-4=m-1+m+3\\ \Leftrightarrow-4=2m+2\Leftrightarrow m=-3\)
3. \(y=\left(m-1\right)x+m+3\\ \Leftrightarrow x+y=mx+m+3\\ \Leftrightarrow x+y-3=m\left(x+1\right)\)
tọa độ điểm cố định là nghiệm của hpt
\(\left\{{}\begin{matrix}x+y-3=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=4\end{matrix}\right.\)
đ cđịnh M(-1;4)
4. \(y=\left(m-1\right)x+m+3\)
+ Khi x=0, y=m+3
+ khi y=0, \(x=\dfrac{-m-3}{m-1}\)
Để \(S=1\Rightarrow\dfrac{-m-3}{m-1}.\left(m+3\right)=2\\ \Leftrightarrow\left(m+3\right)^2=2\left(1-m\right)\\ \Leftrightarrow m^2+8m+7=0\Leftrightarrow\left(m+1\right)\left(m+7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-7\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Cho hàm số y (3m+1 ) x2 có đồ thị là (P) với m là tham số.a) Tính giá trị của m để đồ thị (P) đi qua điểm E left(dfrac{1}{2};dfrac{1}{4}right)b) Tính giá trị của m để đồ thị (P) đi qua điểm F ( x0; y0) với (x0; y0) là nghiệm của hệ phương trình left{{}begin{matrix}3x-4y2-4x+3y-5end{matrix}right. . Vẽ đồ thị (P) thu được.
Đọc tiếp
Cho hàm số y = (3m+1 ) x2 có đồ thị là (P) với m là tham số.
a) Tính giá trị của m để đồ thị (P) đi qua điểm E \(\left(\dfrac{1}{2};\dfrac{1}{4}\right)\)
b) Tính giá trị của m để đồ thị (P) đi qua điểm F ( x0; y0) với (x0; y0) là nghiệm của hệ phương trình \(\left\{{}\begin{matrix}3x-4y=2\\-4x+3y=-5\end{matrix}\right.\) . Vẽ đồ thị (P) thu được.
ĐKXĐ: \(m\ne-\dfrac{1}{3}\)
a) Để (P) đi qua điểm \(E\left(\dfrac{1}{2};\dfrac{1}{4}\right)\) thì
Thay \(x=\dfrac{1}{2}\)và \(y=\dfrac{1}{4}\) vào hàm số \(y=\left(3m+1\right)x^2\), ta được:
\(\left(3m+1\right)\cdot\dfrac{1}{4}=\dfrac{1}{4}\)
\(\Leftrightarrow3m+1=1\)
\(\Leftrightarrow3m=0\)
hay m=0(thỏa ĐK)
b) Ta có: \(\left\{{}\begin{matrix}3x-4y=2\\-4x+3y=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}12x-16y=8\\-12x+9y=-15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7y=-7\\3x-4y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\3x=2+4y=2+4=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy: F(2;1)
Để (P) đi qua điểm F(2;1) thì
Thay x=2 và y=1 vào hàm số \(y=\left(3m+1\right)x^2\), ta được:
\(\left(3m+1\right)\cdot4=1\)
\(\Leftrightarrow3m+1=\dfrac{1}{4}\)
\(\Leftrightarrow3m=-\dfrac{3}{4}\)
\(\Leftrightarrow m=\dfrac{-3}{4}:3=\dfrac{-3}{4}\cdot\dfrac{1}{3}=\dfrac{-1}{4}\)(thỏa ĐK)
Đúng 4
Bình luận (0)
Bài 1: Cho hàm số bậc nhất y(m-1)x+m+3.(d)a)Tìm giá trị của m để đồ thị của hàm số song song với đồ thị hàm số y - 2x + 1 .b) Tìm giá trị của m để đồ thị của hàm số đi qua điểm (1;-4) .c) Tìm điểm cố định mà đồ thị của hàm số luôn đi qua với mọi md) Tìm giá trị của m để đổ thị của hàm số tạo với trục tung và trục hoành một tamgiác có diện tích bằng 1(đvdt ).
Đọc tiếp
Bài 1: Cho hàm số bậc nhất y=(m-1)x+m+3.(d)
a)Tìm giá trị của m để đồ thị của hàm số song song với đồ thị hàm số y = - 2x + 1 .
b) Tìm giá trị của m để đồ thị của hàm số đi qua điểm (1;-4) .
c) Tìm điểm cố định mà đồ thị của hàm số luôn đi qua với mọi m
d) Tìm giá trị của m để đổ thị của hàm số tạo với trục tung và trục hoành một tamgiác có diện tích bằng 1(đvdt ).
Cho hàm số y=(m-1)x +m+3
Tìm giá trị của m để đồ thị của hàm số song song với đồ thị hàm số y=-2x+1Tìm giá trị của m để đồ thị của hàm số đi qua diieemr (1;-4)Tìm điểm cố định mà đồ thị của hàm số luôn đi qua với mọi m.1. Để đồ thị của hàm số y=(m-1)x+m+3 song song với đồ thị hàm số y=-2x+1 thì:
\(\left\{{}\begin{matrix}m-1=-2\\m+3\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m\ne-2\end{matrix}\right.\)
Vậy để 2 đồ thị trên song song với nhau thì m=-1 và m\(\ne\)-2
2. Vì đồ thị đi qua điểm (1;-4) nên ta có:
-4=m-1+m+3
\(\Leftrightarrow\) 2m=-6
\(\Leftrightarrow m=-3\)
Vậy để đồ thị đi qua điểm (1;-4) thì m=-3
Đúng 1
Bình luận (0)
Bài 1 :Cho hàm số y(m-1)x+m+31, Tìm giá trị của m để đồ thị hàm số song song với đồ thị hàm số y-2x+12, Tìm giá trị của m để đồ thị hàm số đi qua điểm (1;-4)3, Tìm điểm cố định mà đồ thị của hàm số luôn đi quaBài 2 : Cho hàm số y(2m-1)x+m-31, Tìm m để đồ thị hàm số đi qua điểm (2;5)2, Cmr đồ thị hàm số luôn đi qua 1 điểm cố định với mọi m. Tìm điểm cố định ấy3, Tìm m để đồ thị hàm số cắt trục hoành tai điểm có hoành độ xsqrt{2}-1
Đọc tiếp
Bài 1 :Cho hàm số y=(m-1)x+m+3
1, Tìm giá trị của m để đồ thị hàm số song song với đồ thị hàm số y=-2x+1
2, Tìm giá trị của m để đồ thị hàm số đi qua điểm (1;-4)
3, Tìm điểm cố định mà đồ thị của hàm số luôn đi qua\
Bài 2 : Cho hàm số y=(2m-1)x+m-3
1, Tìm m để đồ thị hàm số đi qua điểm (2;5)
2, Cmr đồ thị hàm số luôn đi qua 1 điểm cố định với mọi m. Tìm điểm cố định ấy
3, Tìm m để đồ thị hàm số cắt trục hoành tai điểm có hoành độ \(x=\sqrt{2}-1\)
Cho hàm số y=(m-1)x+m+3
a) Tìm giá trị của m để đồ thị hàm số song song với đồ thị hàm số y=-2x+1
b) Tìm gtrị của m để đồ thị của hàm số đi qua điểm (1;-4)
c) Tìm điểm cố định mà đồ thị của hàm số luôn đi qua với mọi m
d) Tìm giá trị của m để đồ thị của hàm số tạo với trục tung và trục hoành một tam giác có diện tích bằng 1(đvdt)
a) y=(m-1)x+m+3 (d1) (a=m-1;b=m+3)
y=-2x+1 (d2) (a' =-2;b' =1)
vì hàm số (d1) song song với hàm số (d2) nên
\(\hept{\begin{cases}a=a'\\b\ne b'\end{cases}}\Leftrightarrow\hept{\begin{cases}m-1=-2\\m+3\ne1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=-1\\m\ne-2\end{cases}}\)
vậy với m= -1 thì hàm số (d1) song song với hàm số (d2)
b) vì hàm số (d1) đi qua điểm (1;-4) nên
x=1 ; y= -4
thay vào (d1) ta có
-4=m-1+m+3 (mình làm tắt ko nhân với 1 nha)
-4=2m+2
-2=2m
m=-1
Cho hàm số ymx+1left(mne0right)left(1right)
1) Tìm m để đồ thị hàm số (1) đi qua điểm Mleft(-1;-1right). Với m tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy
2) Tìm giá trị của m để đồ thị hàm số (1) song song với đường thẳng yleft(m^2-2right)x+2m+3
3) Tìm m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng dfrac{2}{sqrt{5}}.
Đọc tiếp
Cho hàm số \(y=mx+1\left(m\ne0\right)\left(1\right)\)
1) Tìm m để đồ thị hàm số (1) đi qua điểm \(M\left(-1;-1\right)\). Với m tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy
2) Tìm giá trị của m để đồ thị hàm số (1) song song với đường thẳng \(y=\left(m^2-2\right)x+2m+3\)
3) Tìm m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng \(\dfrac{2}{\sqrt{5}}\).
1) \(y=mx+1\left(m\ne0\right)\left(1\right)\) hay \(mx-y+1=0\)
Để đồ thị hàm số \(\left(1\right)\) đi qua điểm \(M\left(-1;-1\right)\) khi và chỉ khi
\(m.\left(-1\right)+1=-1\)
\(\Leftrightarrow-m=-2\)
\(\Leftrightarrow m=2\)
Vậy hàm số \(\left(1\right):y=2x+1\)
Bạn tự vẽ đồ thị nhé!
2) \(y=\left(m^2-2\right)x+2m+3\left(d\right)\)
Để \(\left(1\right)//\left(d\right)\) khi và chỉ khi
\(\left\{{}\begin{matrix}m^2-2=2\\2m+3\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\2m\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\ne-1\end{matrix}\right.\) \(\Leftrightarrow m=\pm2\) thỏa đề bài
3) Khoảng cách từ gốc O đến đồ thị hàm số \(\left(1\right)\) là:
\(d\left(O;\left(1\right)\right)=\dfrac{m.0-0+1}{\sqrt[]{2^2+1^2}}=\dfrac{2}{\sqrt[]{5}}\)
\(\Leftrightarrow\dfrac{0.m+1}{\sqrt[]{5}}=\dfrac{2}{\sqrt[]{5}}\)
\(\Leftrightarrow0m=1\)
\(\Leftrightarrow m\in\varnothing\)
Vậy không có giá trị nào của m để thỏa mãn đề bài,
Đúng 1
Bình luận (0)
Đáp án:
1. Tìm m để đồ thị hàm số (1) đi qua điểm M (−1;−1). Với m tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy
Để đồ thị hàm số (1) đi qua điểm M (−1;−1), ta cần có m(−1)+1=−1. Từ đó ta có m=−2.
Với m=−2, đồ thị hàm số (1) là một đường thẳng có hệ số góc -2 và đi qua điểm M (−1;−1). Ta có thể vẽ đồ thị hàm số như sau:
[Image of the graph of y=-2x+1]
2. Tìm giá trị của m để đồ thị hàm số (1) song song với đường thẳng y (m² - 2) x + 2m+3 =
Hai đường thẳng song song khi hệ số góc của chúng bằng nhau. Do đó, ta có m=m2−2. Từ đó ta có m=2.
3. Tìm m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng 2 √5
Khoảng cách từ gốc O đến đồ thị hàm số (1) là khoảng cách từ điểm (0;1) đến đường thẳng y=mx+1. Khoảng cách này được tính theo công thức:
d=|m|
Do đó, ta có d=2552=2.
Từ đó, ta có m=2.
Kết luận:
Giá trị của m để đồ thị hàm số (1) đi qua điểm M (−1;−1) là m=-2. Giá trị của m để đồ thị hàm số (1) song song với đường thẳng y (m² - 2) x + 2m+3 = là m=2. Giá trị của m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng 2 √5 là m=2.Lưu ý:
Để giải bài toán 1 và 2, ta có thể thay m=-2 vào hàm số (1) và so sánh với tọa độ của điểm M (−1;−1) hoặc tọa độ của một điểm bất kỳ trên đường thẳng y (m² - 2) x + 2m+3 =. Để giải bài toán 3, ta có thể sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.chúc bạn học tốt
Đúng 2
Bình luận (0)
Cảm ơn em đã tham gia hỏi đáp olm.
Trong câu trả lời của Nguyễn Bảo Long là câu coppy chat gpt.
Lần này cô nhắc nhở, lần sau cô xử phạt
Đúng 1
Bình luận (0)
Cho hàm số yleft(m-3right)x
a) Với giá trị nào của m thì hàm số đồng biến ? Nghoc
b) Xác định giá trị của m để đồ thị hàm số đi qua điểm Aleft(1;2right)
c) Xác định giá trị của m để đồ thị hàm số đi qua điểm Bleft(1;-2right)
d) Vẽ đồ thị của hai hàm số ứng với giá trị m tìm được ở câu b), c)
Đọc tiếp
Cho hàm số \(y=\left(m-3\right)x\)
a) Với giá trị nào của m thì hàm số đồng biến ? Nghoc
b) Xác định giá trị của m để đồ thị hàm số đi qua điểm \(A\left(1;2\right)\)
c) Xác định giá trị của m để đồ thị hàm số đi qua điểm \(B\left(1;-2\right)\)
d) Vẽ đồ thị của hai hàm số ứng với giá trị m tìm được ở câu b), c)
Lời giải
a) Hàm số bậc nhất đồng biến khi (a>0) => m-3 >0 => m>3
b) A(1;2) => y(1) =2 => (m-3).1=2 => m=5
c) B(1;-2) => y(1) =-2=> (m-3).1=-2 => m=1
d) 
Đúng 0
Bình luận (0)
a) Hàm số \(y=\left(m-3\right)x\) đồng biến khi \(m-3>0\Leftrightarrow m>3\)
Hàm số \(y=\left(m-3\right)x\) nghịch biến khi \(m-3< 0\Leftrightarrow m< 3\)

Đúng 0
Bình luận (0)
ĐK: m - 3 # 0 <=> m # 0
a) * Hàm số đồng biến khi hệ số a = m - 3 > 0 <=> m > 3
Vậy với m > 3 thì hàm số
y=(m−3)xy=(m−3)x đồng biến.
* Hàm số nghịch biến khi hệ số a=m−3<0⇔m<3a=m−3<0⇔m<3
Vậy với m < 3 thì hàm số y = (m − 3) xy = (m − 3) x nghịch biến.
b) Đồ thị của hàm số y = (m − 3) xy = (m − 3) x đi qua điểm A(1;2) nên tọa độ điểm A nghiệm đúng phương trình hàm số.
Ta có: 2 = (m − 3) 1 ⇔ 2 = m − 3 ⇔ m = 52 = (m − 3) 1 ⇔ 2 = m − 3 ⇔ m = 5.
Giá trị m = 5 thỏa mãn điều kiện bài toán .
Vậy với m = 5 thì đồ thị hàm số y = (m − 3) xy =(m − 3) x đi qua điểm A(1;2)
c) Đồ thị của hàm số y = (m − 3) xy = (m − 3) x đi qua điểm B(1;-2) nên tọa độ điểm B nghiệm đúng phương trình hàm số.
Ta có : −2 = (m − 3) 1 ⇔ −2 = m − 3 ⇔ m = 1 − 2 = (m − 3) 1 ⇔ − 2 = m − 3 ⇔ m = 1
Giá trị m = 1 thỏa mãn điều kiện bài toán .
Vậy với m = 1 thì đồ thị hàm số y = (m − 3) xy = (m − 3) x đi qua điểm B(1;-2).
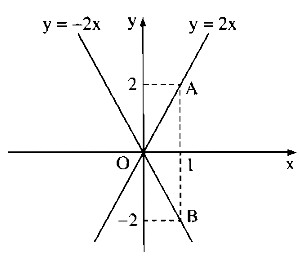
d) Khi m = 5 thì ta có hàm số: y = 2x
Khi m = 1 thì ta có hàm số: y = -2x
*Vẽ đồ thị của hàm số y = 2x
Cho x = 0 thì y = 0. Ta có: O(0;0)
Cho x = 1 thì y = 2. Ta có: A(1;2)
Đường thẳng OA là đồ thị hàm số y = 2x.
*Vẽ đồ thị của hàm số
Cho x = 0 thì y = 0. Ta có : O(0;0)
Cho x = 1 thì y = -2 . Ta có : B(1;-2)
Đường thẳng OB là đồ thị của hàm số y = -2x.
Đúng 0
Bình luận (0)
Cho 2 hàm số \(y=\left(3m+2\right)x+5\) với \(m\ne-1\), \(y=-x-1\) có đồ thị cắt nhau tại điểm \(A\left(x;y\right)\). Tìm các giá trị \(m\) để biểu thức \(P=y^2+2x-2019\) đạt giá trị nhỏ nhất.
Hai đồ thị \(y=\left(3m+2\right)x+5\) và \(y=-x-1\) cắt nhau
\(\Rightarrow3m+2\ne-1\Rightarrow m\ne-1\)
Khi đó ta có giao điểm 2 đồ thị là \(A=\left(x;y\right)=\left(x;-x-1\right)\)
\(P=y^2+2x-2019=\left(-x-1\right)^2+2x-2019=x^2+4x-2018\\ =\left(x+2\right)^2-2022\ge-2022\)
Dấu = xảy ra \(\Leftrightarrow x+2=0\Leftrightarrow x=-2\Leftrightarrow y=1\)
\(\Rightarrow1=\left(3m+2\right)\left(-2\right)+5\Rightarrow-6m=0\Rightarrow m=0\left(TM\right)\)
Đúng 3
Bình luận (0)






























