Giải phương trình:
\(3tan2x-\dfrac{3}{cos2x}-2\dfrac{1-cotx}{1+cotx}+2cos2x=0\)
giải phương trình:
3tan2x + 2cos2x = \(\dfrac{3}{cos2x}\) + 2tan (x- \(\dfrac{\pi}{4}\))
Điều kiện xác định : sin4x ≠ 0
3tan2x + 2cos2x = \(\dfrac{3}{cos2x}\) + 2 \(\dfrac{sin\left(x-\dfrac{\pi}{4}\right)}{cos\left(x-\dfrac{\pi}{4}\right)}\)
⇔ 3tan2x + 2cos2x = \(\dfrac{3}{cos2x}\) + 2 \(\dfrac{sinx-cosx}{sinx+cosx}\)
⇒ 3tan2x . cos2x + 2cos22x = 3 + 2\(\dfrac{sinx-cosx}{sinx+cosx}\).cos2x
⇒ 3sin2x + 2cos22x = 3 + 2. \(\dfrac{sinx-cosx}{sinx+cosx}\).(cosx - sinx)(cosx + sinx)
⇒ 3sin2x + 2cos22x = 3 - 2(sinx - cosx)2
⇔ 3sin2x + 2cos22x = 3 - 2 . (1 - sin2x)
⇔ 3sin2x + 2 - 2sin22x = 3 - 2 + 2sin2x
⇔ - 2sin22x + sin2x + 1 = 0
⇔ \(\left[{}\begin{matrix}sin2x=1\\sin2x=-\dfrac{1}{2}\end{matrix}\right.\)
Loại sin2x = 1 vì khi đó cos2x = 0 (vi phạm ĐKXĐ)
⇔ sin2x = \(-\dfrac{1}{2}\)
Giải nốt nhé
Giải phương trình:
\(\dfrac{\sqrt{3}}{Cos^2x}+\dfrac{4+2Sin2x}{Sin2x}-2\sqrt{3}=2\left(Cotx+1\right)\)
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{\sqrt{3}}{cos^2x}+2+\dfrac{2}{sinx.cosx}-2\sqrt{3}=2\left(\dfrac{1}{tanx}+1\right)\)
\(\Leftrightarrow\sqrt{3}\left(1+tan^2x\right)+\dfrac{\dfrac{2}{cos^2x}}{\dfrac{sinx.cosx}{cos^2x}}+2-2\sqrt{3}=2\left(\dfrac{1}{tanx}+1\right)\)
\(\Leftrightarrow\sqrt{3}tan^2x+\dfrac{2\left(1+tan^2x\right)}{tanx}+2-\sqrt{3}=\dfrac{2}{tanx}+2\)
\(\Leftrightarrow\sqrt{3}tan^3x+2\left(1+tan^2x\right)-\sqrt{3}tanx=2\)
\(\Leftrightarrow\sqrt{3}tan^3x+2tan^2x-\sqrt{3}tanx=0\)
\(\Leftrightarrow...\)
Giải phương trình cos 2 x c o t x - π 3 = 0
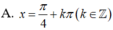
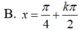
![]()
![]()
Giải các phương trình sau:
\(a,cos3x=-cos\left(x+\dfrac{\pi}{3}\right)\)
\(b,tanx+cotx=0\)
a) cos3x = \(cos\left(\pi-x-\dfrac{\pi}{3}\right)\)
<=> cos3x = \(cos\left(\dfrac{2\pi}{3}-x\right)\)
<=> 3x = \(\dfrac{2\pi}{3}-x\) hoặc 3x = \(\dfrac{-2\pi}{3}+x\)
<=> 4x = \(\dfrac{2\pi}{3}+k2\pi\) hoặc 2x = \(\dfrac{-2\pi}{3}+k2\pi\)
<=> x = \(\dfrac{\pi}{6}+\dfrac{k\pi}{2}\) hoặc x = \(\dfrac{-\pi}{3}+k\pi\)
<=> x = \(\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{2};\dfrac{-\pi}{3}+k\pi;k\in Z\right\}\)
b ) Điều kiện sinx\(\ne0;cosx\ne0\)
<=> sin2x\(\ne0\) <=> x \(\ne\dfrac{k\pi}{2}\);k\(\in Z\)
tanx + cotx =0
<=> tan2x + tanx =0
<=> tanx(tanx+1)=0
<=> tanx=0 hoặc tanx = -1
<=> x=\(k\pi\) (loại) hoặc x = \(\dfrac{-\pi}{4}+k\pi\)
Vậy x = \(\dfrac{-\pi}{4}+k\pi;k\in Z\)
1) cosx\(^2\)+sinx=0
2) 2cos\(^2\)x-cos2x+cosx=0
3) sin\(^2\)x-3cos2x-2=0
4) tanx+\(\dfrac{2}{cotx}\)=0
3.
\(\dfrac{1}{2}-\dfrac{1}{2}cos2x-3cos2x-2=0\)
\(\Leftrightarrow-7cos2x-3=0\)
\(\Rightarrow cos2x=-\dfrac{3}{7}\)
\(\Rightarrow2x=\pm arccos\left(-\dfrac{3}{7}\right)+k2\pi\)
\(\Rightarrow x=\pm\dfrac{1}{2}arccos\left(-\dfrac{3}{7}\right)+k\pi\)
4.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(tanx+2tanx=0\)
\(\Rightarrow3tanx=0\)
\(\Rightarrow tanx=0\)
\(\Rightarrow x=k\pi\) (loại do ĐKXĐ)
Vậy pt đã cho vô nghiệm
1.
\(\Leftrightarrow1-sin^2x+sinx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1+\sqrt{5}}{2}>1\left(loại\right)\\sinx=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\\x=\pi-arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\end{matrix}\right.\) (\(k\in Z\))
2.
\(2cos^2x-\left(2cos^2x-1\right)+cosx=0\)
\(\Leftrightarrow cosx+1=0\)
\(\Leftrightarrow cosx=-1\)
\(\Leftrightarrow x=\pi+k2\pi\) (\(k\in Z\))
tìm txd của hàm số
y = \(\dfrac{sin\left(x-\dfrac{\pi}{3}\right)}{cos2x+1}+cotx\)
Lời giải:
ĐKXĐ: \(\left\{\begin{matrix}
\cos 2x+1\neq 0\\
\sin x\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
2x\neq \pm \pi +2k\pi \\
x\neq n\pi \end{matrix}\right.\) với mọi $k,n\in\mathbb{Z}$
\(\Leftrightarrow \left\{\begin{matrix} x\neq \frac{k}{2}\pi, \text{k nguyên lẻ} \\ x\neq n\pi, \text{n nguyên bất kỳ} \end{matrix}\right.\)
Giải các phương trình sau:
a,\(\dfrac{sin2x+cosx-\sqrt{3}\left(cos2x+sinx\right)}{2sin2x-\sqrt{3}}\)
=1
b,
(2cosx-1)cotx=\(\dfrac{3}{sinx}+\dfrac{2sinx}{cosx-1}\)
a.\(\dfrac{sin2x+cosx-\sqrt{3}\left(cos2x+sinx\right)}{2sin2x-\sqrt{3}}=1\left(1\right)\)
ĐKXĐ: sin2x≠\(\dfrac{\sqrt{3}}{2}\)
(1) ⇔ sin2x + cosx - \(\sqrt{3}\) ( cos2x + sinx) = 2sin2x - \(\sqrt{3}\)
⇔cosx - \(\sqrt{3}\) sinx = \(\sqrt{3}\) cos2x + sin2x +\(\sqrt{3}\)
⇔\(\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{\sqrt{3}}{2}cos2x+\dfrac{1}{2}sin2x+\dfrac{\sqrt{3}}{2}\)
⇔\(sin\left(\dfrac{\Pi}{6}-x\right)=sin\left(2x+\dfrac{\Pi}{3}\right)-sin\dfrac{\Pi}{3}\)
⇔\(sin\left(\dfrac{\Pi}{6}-x\right)=2cos\left(x+\dfrac{\Pi}{3}\right)sinx\)
⇔\(sin\left(\dfrac{\Pi}{6}-x\right)=2sin\left(\dfrac{\Pi}{6}-x\right)sinx\)
⇔\(sin\left(\dfrac{\Pi}{6}-x\right)\left(2sinx-1\right)=0\)
Đến đây tự giải tiếp nha nhớ đối chiếu đk.
b.\(\left(2cosx-1\right)cotx=\dfrac{3}{sinx}+\dfrac{2sinx}{cosx-1}\left(1\right)\)
ĐKXĐ: sinx≠0 và cosx≠1
(1)⇔\(\left(2cosx-1\right)\dfrac{cosx}{sinx}=\dfrac{3}{sinx}+\dfrac{2sinx}{cosx-1}\)
⇔cosx(2cosx-1)(cosx-1) = 3(cosx-1) + 2sin2x
⇔2cos3x - cos2x - 2cosx +1 = 0
⇔ (cosx-1)(cosx+1)(2cosx-1)=0
1> 1 + sinx + cosx + sin2x + cos2x = 0
2> cos2x + 3sin2x + 5 sinx - 3cosx = 3
3> \(\dfrac{\sqrt{2}*(cosx - sinx)}{cotx - 1}\) = \(\dfrac{1}{tanx + cot2x}\)
4> (2cosx - 1)*(2sinx + cosx) = sin2x - sinx
1. cho 180 độ < x < 250 độ. kết quả đúng là
A. sinx>0, cosx>0
B. sinx<0, cosx<0
C. sinx>0, cosx<0
D. sinx<0, cosx>0
2. cho \(\dfrac{3\pi}{4}\) <x< \(\dfrac{3\pi}{2}\) kết quả đúng là
A. tanx>0, cotx>0
B. tanx<0, cotx<0
C. tanx>0, cotx<0
D. tanx<0, cotx>0
3.
cho 2\(\pi\) < x <\(\dfrac{5\pi}{2}\) kết quả đúng là
A. tanx>0, cotx>0
B. tanx<0, cotx<0
C. tanx>0, cotx<0
D. tanx<0, cotx>0
4.
cho 630 độ < x <720 độ. kết quả đúng là
A. sinx>0, cosx>0
B. sinx<0, cosx<0
C. sinx>0, cosx<0
D. sinx<0, cosx>0