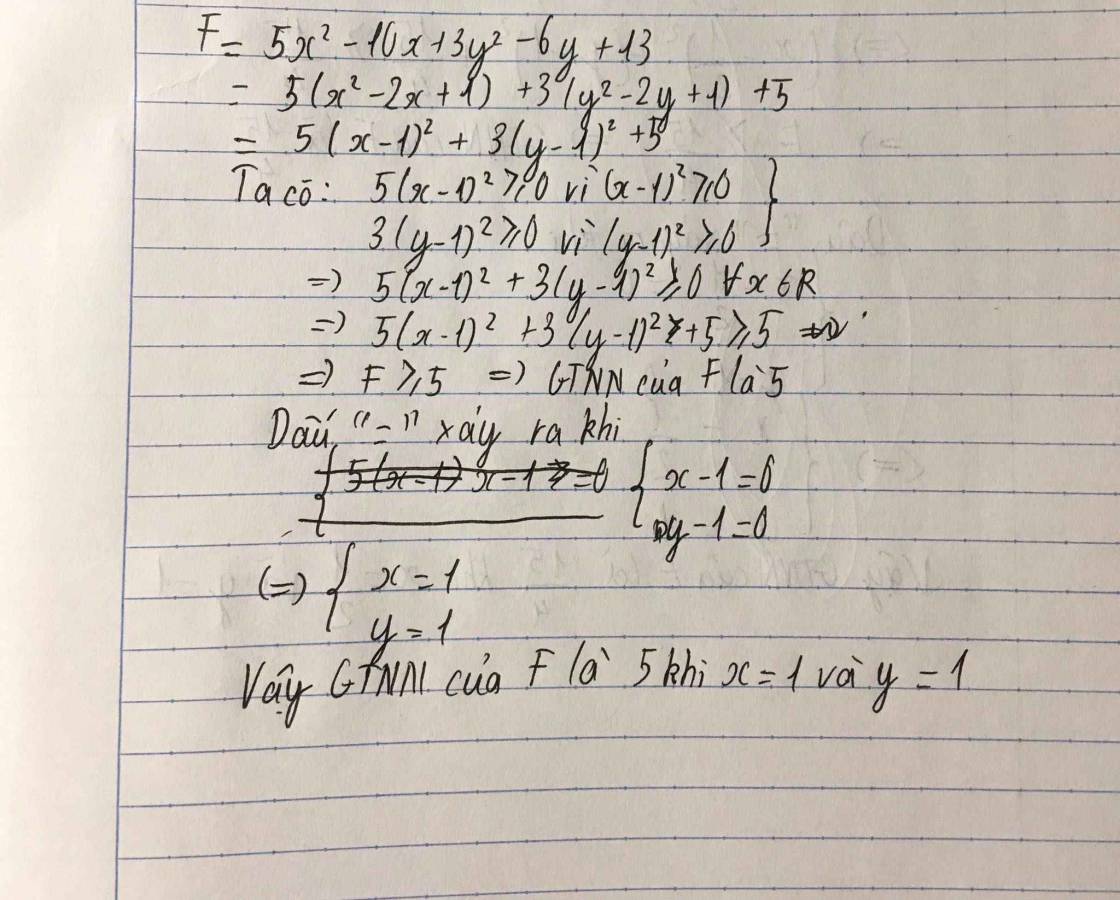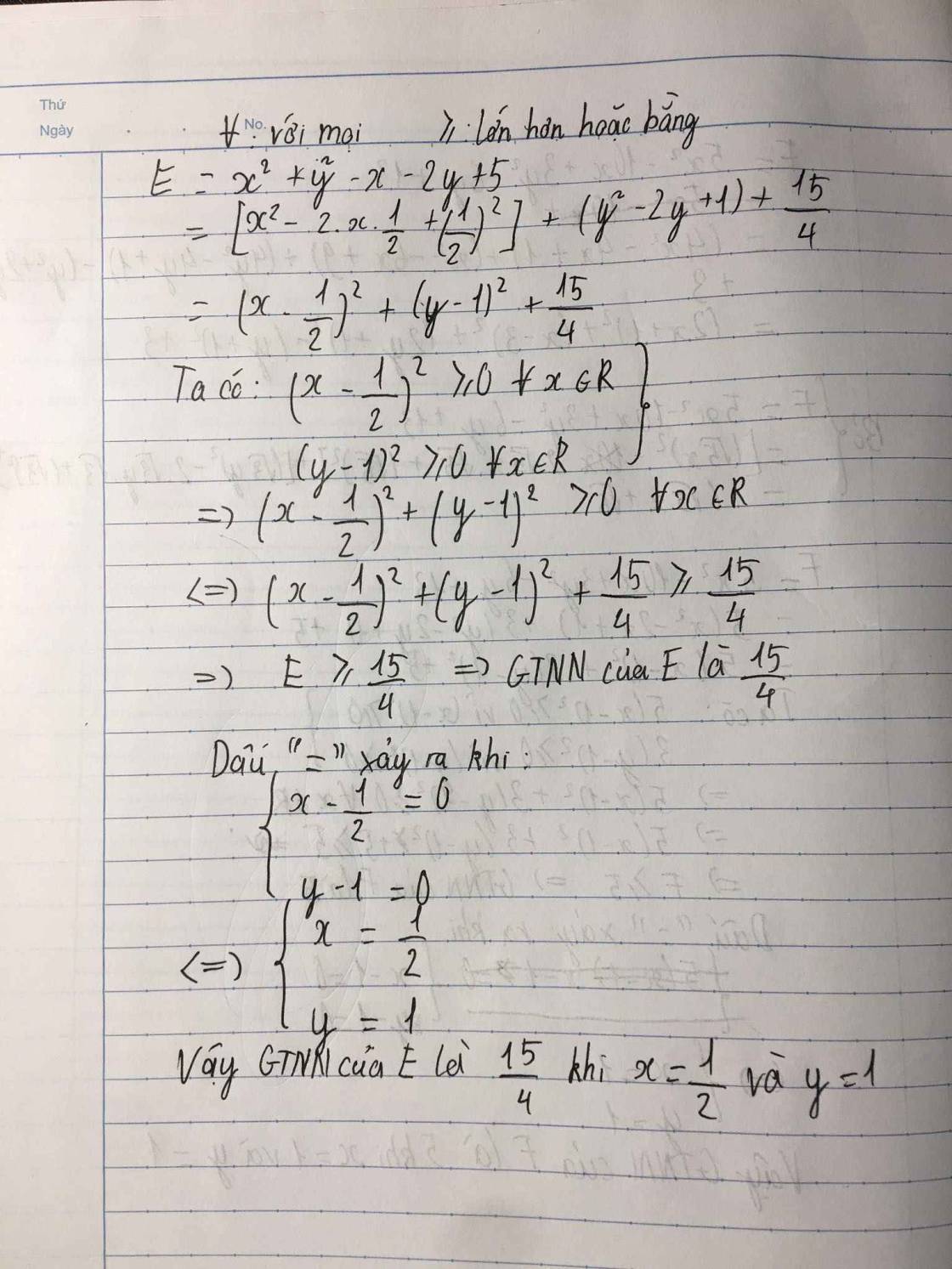Bạn chép thiếu đề à??

2x² + 2y² + 2xy - 6y + 21

= (x² + 2xy + y²) - 2(x + y) + 1 + (x² + 2x + 1) + (y² - 4y + 4) + 15

= (x + y)² - 2(x + y) + 1 + (x + 1)² + (y - 2)² + 15

= (x + y - 1)² + (x + 1)² + (y - 2)² + 15 \(\ge15\)

Vậy GTNN là 15 đạt được khi x = - 1, y = 2

b) Ta có: \(B=x^2+2x+y^2-4y+6\)

\(=x^2+2x+1+y^2-4y+4+1\)

\(=\left(x+1\right)^2+\left(y-2\right)^2+1\ge1\forall x,y\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)

Vậy: \(B_{min}=1\) khi (x,y)=(-1;2)

c) Ta có: \(C=4x^2+4x+9y^2-6y-5\)

\(=4x^2+4x+1+9y^2-6y+1-7\)

\(=\left(2x+1\right)^2+\left(3y-1\right)^2-7\ge-7\forall x,y\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)

Vậy: \(C_{min}=-7\) khi \(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)

\(A=2x^2+x=2\left(x^2+\dfrac{1}{2}x\right)=2\left(x^2+2.\dfrac{1}{4}x+\dfrac{1}{16}-\dfrac{1}{16}\right)\)

\(=2\left[\left(x+\dfrac{1}{4}\right)^2-\dfrac{1}{16}\right]\ge-\dfrac{1}{8}\) dấu"=' xảy ra<=>x=\(-\dfrac{1}{4}\)

\(B=x^2+2x+y^2-4y+6\)

\(=x^2+2x+1+y^2-4y+4+1=\left(x+1\right)^2+\left(y-2\right)^2+1\)

\(\ge1\) dấu"=" xảy ra<=>x=-1;y=2

\(C=4x^2+4x+9y^2-6y-5\)

\(=4x^2+4x+1+9y^2-6y+1-7\)

\(=\left(2x+1\right)^2+\left(3y-1\right)^2-7\ge-7\)

dấu"=" xảy ra<=>x=\(-\dfrac{1}{2},y=\dfrac{1}{3}\)

\(D=\left(2+x\right)\left(x+4\right)-\left(x-1\right)\left(x+3\right)^2\)

=\(x^2+6x+8-\left(x-1\right)\left(x+3\right)^2\)

\(=\left(x+3\right)^2-1-\left(x-1\right)\left(x+3\right)^2\)

\(=\left(x+3\right)^2\left(2-x\right)-1\ge-1\)

dấu"=" xảy ra\(< =>\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)

a.

\(A=\left(x^4+y^2+1-2x^2y+2x^2-2y\right)+2\left(y^2-2y+1\right)+2026\)

\(A=\left(x^2-y+1\right)^2+2\left(y-1\right)^2+2026\ge2026\)

\(A_{min}=2026\) khi \(\left(x;y\right)=\left(0;1\right)\)

b.

Đặt \(x-1=t\Rightarrow x=t+1\)

\(\Rightarrow A=\dfrac{3\left(t+1\right)^2-8\left(t+1\right)+6}{t^2}=\dfrac{3t^2-2t+1}{t^2}=\dfrac{1}{t^2}-\dfrac{2}{t}+3=\left(\dfrac{1}{t}-1\right)^2+2\ge2\)

\(A_{min}=2\) khi \(t=1\Rightarrow x=2\)

\(A=\dfrac{3x^2-8x+6}{x^2-2x+1}=\dfrac{3x^2-8x+6}{\left(x-1\right)^2}=\dfrac{2\left(x-1\right)^2+\left(x-2\right)^2}{\left(x-1\right)^2}=2+\dfrac{\left(x-2\right)^2}{\left(x-1\right)^2}\ge2\)

Dấu \("="\Leftrightarrow x=2\)

a) \(A=x^2+2y^2+2xy+4x+6y+19\)

\(=\left[\left(x^2+2xy+y^2\right)+2.\left(x+y\right).2+4\right]+\left(y^2+2y+1\right)+14\)

\(=\left[\left(x+y\right)^2+2\left(x+y\right).2+2^2\right]+\left(y+1\right)^2+14\)

\(=\left(x+y+2\right)^2+\left(y+1\right)^2+14\ge14\)

Dấu "=" xảy ra khi \(\hept{\begin{cases}x+y+2=0\\y=-1\end{cases}}\Leftrightarrow x=y=-1\)

b)Đề có gì đó sai sai...

c) Tương tự câu b,em cũng thấy sai sai...HÓng cao nhân giải ạ!

b) \(P=2x^2+y^2+2xy-2y-4\)

\(\Leftrightarrow2P=4x^2+2y^2+4xy-4y-8\)

\(\Leftrightarrow2P=\left(4x^2+4xy+y^2\right)+\left(y^2-4y+4\right)-12\)

\(\Leftrightarrow2P=\left(2x+y\right)^2+\left(y-2\right)^2-12\ge-12\forall x;y\)

Có \(2P\ge-12\Leftrightarrow P\ge-6\)

Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}2x+y=0\\y-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-1\\y=2\end{cases}}}\)

a, xem lại đề 

\(b,x^2-4x+y^2-6y+1\\ =\left(x^2-4x+4\right)+\left(y^2-6y+9\right)-12\\ =\left(x-2\right)^2+\left(y-3\right)^2-12\ge-12\)

Dấu "=" xảy ra\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)

Vậy ...

\(c,x^2-4xy+5y^2-2y+5\\ =\left(x^2-4xy+4y^2\right)+\left(y^2-2y+1\right)+4\\ =\left(x-2y\right)^2+\left(y-1\right)^2+4\ge4\)

Dấu "=" xảy ra\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

Vậy ...

a, 

Dấu "=" xảy ra⇔{x=2y=3⇔{x=2y=3

Vậy ...

Dấu "=" xảy ra⇔{x=2y=1⇔{x=2y=1

Vậy ...

\(2x^2+2y^2-2xy-6y+21\)

\(2A=4x^2+4y^2-4xy-12y+42\)

\(=4x^2-4xy+4y^2-12y+42\)

\(=4x^2-4xy+y^2+3y^2-12y+42\)

\(=\left(4x^2-4xy+y^2\right)+\left(3y^2-12y+42\right)\)

\(=\left(2x-y\right)^2+3\left(y^2-4x+4\right)+30\)

\(=\left(2x-y\right)^2+3\left(y-2\right)^2+30\ge30\)

Vậy GTNN là 30

Cho mk sủa lại tí :

\(2A=4x^2+4y^2-4xy-12y+42\)

\(=4x^2-4xy+4y^2-12+42\)

\(=4x^2-4xy+y^2+3y^2-12y+42\)

\(=\left(2x-y\right)^2+3\left(y-2\right)^2+30\ge30\)

\(\Rightarrow2A\ge30\Rightarrow A\ge15\Rightarrow\)GTNN là 15