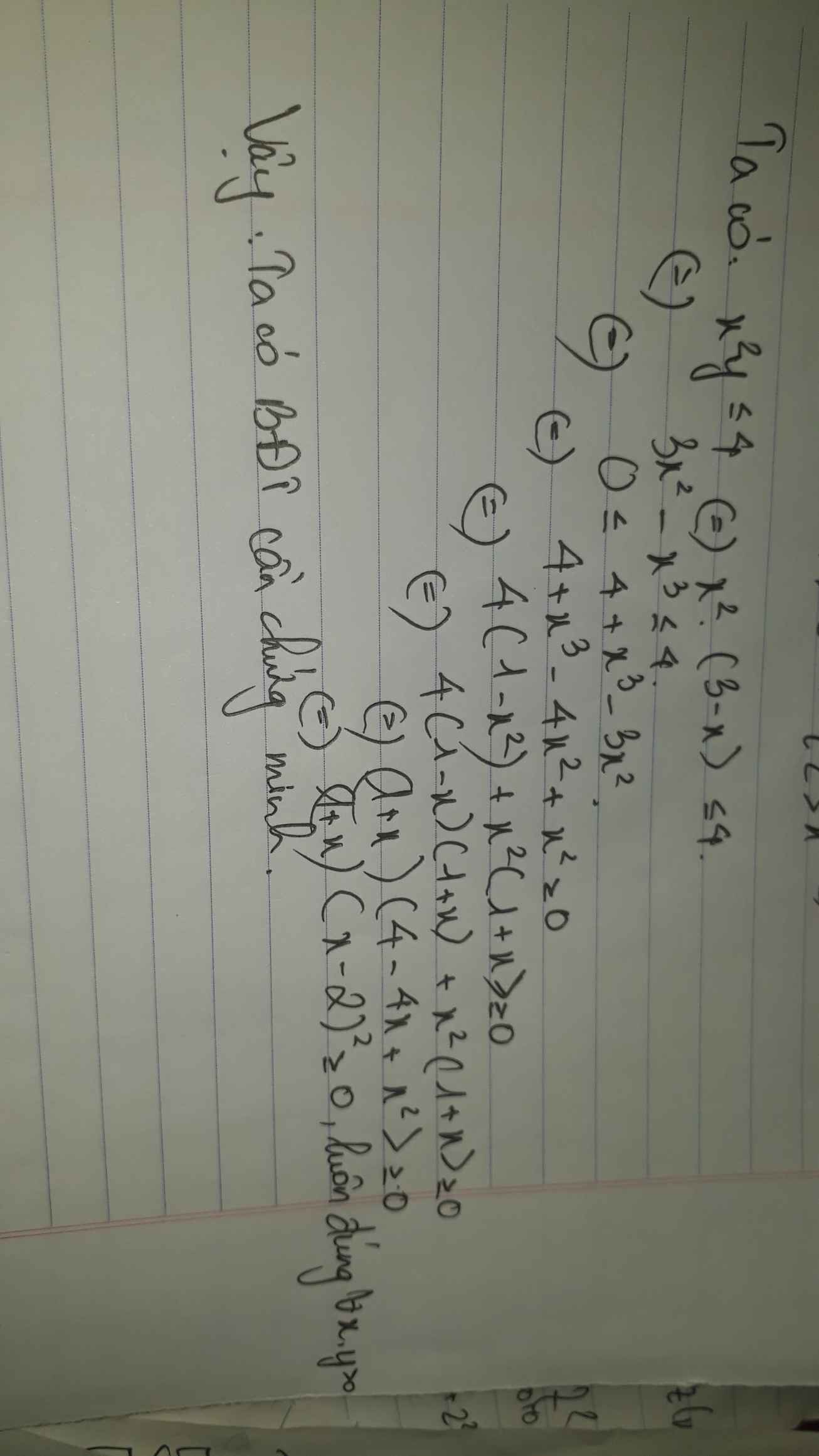\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)

\(< =>\left(\dfrac{1}{a}+\dfrac{1}{b}\right).\left(a+b\right)\ge4\)

\(< =>1+\dfrac{b}{a}+\dfrac{a}{b}+1\ge4\)

\(< =>2+\dfrac{a}{b}+\dfrac{b}{a}\ge4\)(luôn đúng với mọi a,b là số thực dương)

Thật vậy có \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{a}{b}.\dfrac{b}{a}}=2\)(BĐT Cosi)

\(=>2+\dfrac{a}{b}+\dfrac{b}{a}\ge2+2=4\left(đpcm\right)\)

dấu"=" xảy ra<=>a=b

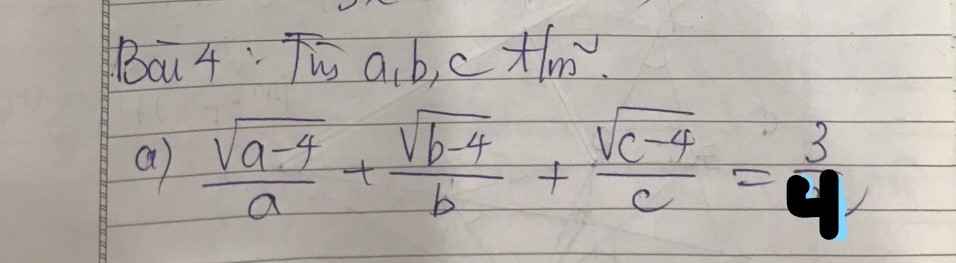
\(\dfrac{\sqrt{a-4}}{a}+\dfrac{\sqrt{b-4}}{b}+\dfrac{\sqrt{c-4}}{c}=\dfrac{3}{4}\) (ĐK: \(a\ge4;b\ge4;c\ge4\))

Áp dụng AM-GM có:
\(2\sqrt{4\left(a-4\right)}\le4+a-4=a\)

\(\Rightarrow\dfrac{\sqrt{a-4}}{a}\le\dfrac{1}{4}\)

Tương tự cũng có: \(\dfrac{\sqrt{b-4}}{b}\le\dfrac{1}{4}\);\(\dfrac{\sqrt{c-4}}{c}\le\dfrac{1}{4}\)

Cộng vế với vế \(\Rightarrow VT\le\dfrac{3}{4}\)

Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}4=a-4\\4=b-4\\4=c-4\end{matrix}\right.\)\(\Rightarrow a=b=c=8\) (tm)

Vậy...

Em tham khảo nhé, công thức AM-GM thì điều kiện là các số không âm, còn công thức Bunhiacopxki thì các số thuộc tập hợp số thực là được.

phải chứng minh

chứng minh nó thì phải cm am-gm 2 số sau đó là 4 số @@ dài lắm

xD

Có: \(\frac{x^2-z^2}{y+z}+\frac{y^2-x^2}{z+x}+\frac{z^2-y^2}{x+y}\)(1)

\(=\frac{\left(x-z\right)\left(x+z\right)}{y+z}+\frac{\left(y-x\right)\left(x+y\right)}{z+x}+\frac{\left(z-y\right)\left(y+z\right)}{x+y}\)

\(\left(1\right)=S_1\left(x-z\right)^2+S_2\left(y-x\right)^2+S_3\left(z-y\right)^2\)

Trong đó:

\(\hept{\begin{cases}S_1=\frac{x+z}{\left(y+z\right)\left(x-z\right)}\\S_2=\frac{x+y}{\left(z+x\right)\left(y-x\right)}\\S_3=\frac{y+z}{\left(x+y\right)\left(z-y\right)}\end{cases}}\)

Giả sử: \(x\ge y\ge z\)( x,y,z lớn hơn 0)

Có: \(S_1=\frac{x+z}{\left(y+z\right)\left(x-z\right)}\ge0\)

Xét: \(S_1+S_2=\frac{x+z}{\left(y+z\right)\left(x-z\right)}-\frac{x+y}{\left(x+z\right)\left(x-y\right)}=\frac{\left(x+z\right)^2+\left(x+y\right)\left(y+z\right)^2+\left(y+z\right)\left(y-z\right)\left(2x+y+z\right)}{.....}\ge0\)

Xét tiếp \(S_1+S_3\)là xong

Không biết đúng k tại mình hơi yếu

*Nếu được giả sử như bạn Cà Bùi thì bài làm của em như sau,mong mọi người góp ý ạ!

Ta có: \(VT=\frac{x^2-z^2}{y+z}+\frac{y^2-x^2}{z+x}-\frac{x^2-z^2+y^2-x^2}{x+y}\)

\(=\left(x^2-z^2\right)\left(\frac{x+y-y-z}{\left(x+y\right)\left(y+z\right)}\right)+\left(y^2-x^2\right)\left(\frac{x+y-z-x}{\left(z+x\right)\left(x+y\right)}\right)\) (nhóm các số thích hợp + quy đồng)

\(=\frac{\left(x+z\right)\left(x-z\right)^2}{\left(x+y\right)\left(y+z\right)}+\frac{\left(y-x\right)\left(y-z\right)}{\left(z+x\right)}\)

Do a, b, c có tính chất hoán vị, nên ta giả sử y là số lớn nhất. Khi đó vế trái không âm hay ta có đpcm.

Bn giỏi quá !

Bạn lên google gõ các chuyên đề về BĐT Bunhiacopxky có rất nhiều mà.

$(a_1^2+a_2^2+...+a_n^2)(b_1^2+b_2^2+...+b_n^2)\geq (a_1b_1+a_2b_2+...+a_nb_n)^2$
Dấu "=" xảy ra khi:

$\frac{a_1}{b_1}=\frac{a_2}{b_2}=...=\frac{a_n}{b_n}$