Rút gọn biểu thức: cota+ tana/ 1+ tan2a.tana

Những câu hỏi liên quan
Biểu thức (cota + tana)2 bằng A. B. cot2a + tan2a. C . D. cot2a.tan2a + 2.
Đọc tiếp
Biểu thức (cota + tana)2 bằng
A. 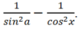
B. cot2a + tan2a.
C .![]()
D. cot2a.tan2a + 2.
Chọn C.
Ta có: cota + tana) 2 = cot2a + 2.cota.tana + tan2a
= (cot2a + 1) + (tan2a + 1)
![]()
Đúng 0
Bình luận (0)
Biết sina = \(\frac{2}{5}\) . Tính giá trị biểu thức : \(\frac{cota-tana}{cota+tana}\)
Ta có : \(\sin^2a+\cos^2a=1\Rightarrow\cos a=\frac{\sqrt{21}}{5}\)
Ta có : \(\frac{\cot a-\tan a}{\cot a+\tan a}=\frac{\frac{\cos a}{\sin a}-\frac{\sin a}{\cos a}}{\frac{\cos a}{\sin a}+\frac{\sin a}{\cos a}}\\ =\frac{\frac{\frac{\sqrt{21}}{5}}{\frac{2}{5}}-\frac{\frac{2}{5}}{\frac{\sqrt{21}}{5}}}{\frac{\frac{\sqrt{21}}{5}}{\frac{2}{5}}+\frac{\frac{2}{5}}{\frac{\sqrt{21}}{5}}}=\frac{17}{25}=0,68\)
Đúng 0
Bình luận (1)
cho sin a= 1/3. Tính giá tị của biểu thức A= cota-tana/ tan+2cota
\(A=\dfrac{cota-tana}{tana+2\cdot cota}\)
\(=\dfrac{\dfrac{cosa}{sina}-\dfrac{sina}{cosa}}{\dfrac{sina}{cosa}+2\cdot\dfrac{cosa}{sina}}\)
\(=\dfrac{cos^2a-sin^2a}{sina\cdot cosa}:\dfrac{sin^2a+2\cdot cos^2a}{sina\cdot cosa}\)
\(=\dfrac{cos^2a-sin^2a}{sin^2a+2\cdot cos^2a}\)
\(=\dfrac{1-2\cdot sin^2a}{sin^2a+2\left(1-sin^2a\right)}\)
\(=\dfrac{1-2\cdot sin^2a}{-sin^2a+2}\)
\(=\dfrac{1-2\cdot\left(\dfrac{1}{3}\right)^2}{-\left(\dfrac{1}{3}\right)^2+2}=\dfrac{1-\dfrac{2}{9}}{-\dfrac{1}{9}+2}=\dfrac{7}{9}:\dfrac{17}{9}=\dfrac{7}{17}\)
Đúng 1
Bình luận (0)
Chứng minh rằng giá trị của biểu thức A dưới đây không phụ thuộc vài số đo góc a
A=(tana + cota)bình phương - (tana-cota)bình phương
a/ cho sin a = \(\frac{-3}{5}\) và \(\frac{-\pi}{2}< a< 0\) . Tính cos a , tan a
b/ Rút gọn biểu thức : A = \(\frac{tana+cota}{1+tan^2a}\)
\(-\frac{\pi}{2}< a< 0\Rightarrow cosa>0\)
\(\Rightarrow cosa=\sqrt{1-sin^2a}=\frac{4}{5}\)
\(tana=\frac{sina}{cosa}=-\frac{3}{4}\)
\(A=\frac{tana+cota}{1+tan^2a}=\frac{tana+\frac{1}{tana}}{1+tan^2a}=\frac{1+tan^2a}{\left(1+tan^2a\right)tana}=\frac{1}{tana}=cota\)
Đúng 0
Bình luận (0)
3; cho tana-cota=3 . tính giá trị các biểu thức sau :
a; A= tan2a + cot2a
Cho Sin a = \(\dfrac{3}{5}\) và \(90^o< a< 180^o\). Gi á trị của biểu thức E = \(\dfrac{Cota-2tana}{tana+3cota}\) là
Ta có: `sin^2 a+cos^2 a=1`
`=>cos a=+- 4/5` Mà `90^o < a < 180^o`
`=>cos a=-4/5`
`=>{(tan a=[sin a]/[cos a]=-3/4),(cot a=1/[tan a]=-4/3):}`
Có: `E=[cot a-2tan a]/[tan a+3cot a]`
`E=[-4/3+2. 3/4]/[-3/4- 3. 4/3]=-2/57`.
Đúng 1
Bình luận (0)
Sina = 2/3
Tính :
Cota - Tana / Cota + Tana = ??
#toán10
Tinh cac gia tri bieu thuc sau:
A= (cota+tana)/(cota-tana) voi sina=3/5
B= (sin^2a-cos^2a)/(sin^2a-3cos^2a) voi cota=-1/3
C1=sin^2a+2cos^2a va C2= sin^4a-cos^4a voi tana=-2
Ai giup minh voii. Minh cam on nhieuu!
\(sina=\frac{3}{5}\Rightarrow sin^2a=\frac{9}{25}\) ; \(cos^2a=1-\frac{9}{25}=\frac{16}{25}\)
\(A=\frac{cota+tana}{cota-tana}=\frac{sina.cosa\left(cota+tana\right)}{sina.cosa\left(cota-tana\right)}=\frac{cos^2a+sin^2a}{cos^2a-sin^2a}=\frac{1}{cos^2a-sin^2a}=\frac{1}{\frac{16}{25}-\frac{9}{25}}=\frac{25}{7}\)
\(B=\frac{sin^2a-cos^2a}{sin^2a-3cos^2a}=\frac{\frac{sin^2a}{sin^2a}-\frac{cos^2a}{sin^2a}}{\frac{sin^2a}{sin^2a}-\frac{3cos^2a}{sin^2a}}=\frac{1-cot^2a}{1-3cot^2a}=\frac{1-\left(-\frac{1}{3}\right)^2}{1-3\left(-\frac{1}{3}\right)^2}=\)
\(C_1=sin^2a+cos^2a+cos^2a=1+cos^2a=1+\frac{1}{1+tan^2a}=1+\frac{1}{1+\left(-2\right)^2}\)
\(C_2=\left(sin^2a+cos^2a\right)\left(sin^2a-cos^2a\right)=sin^2a-cos^2a=1-2cos^2a\)
\(=1-\frac{2}{1+tan^2a}=1-\frac{2}{1+\left(-2\right)^2}\)
Đúng 1
Bình luận (0)


















