tính giá trị biểu thức 14x2 - 21x + 20 biết 2x2 - 3x + 5

Những câu hỏi liên quan
tính giá trị biểu thức 14x2 - 21x + 20 biết 2x2 - 3x + 5
Đề thiếu giá trị nhé bạn, bạn thay giá trị đã cho vào là được
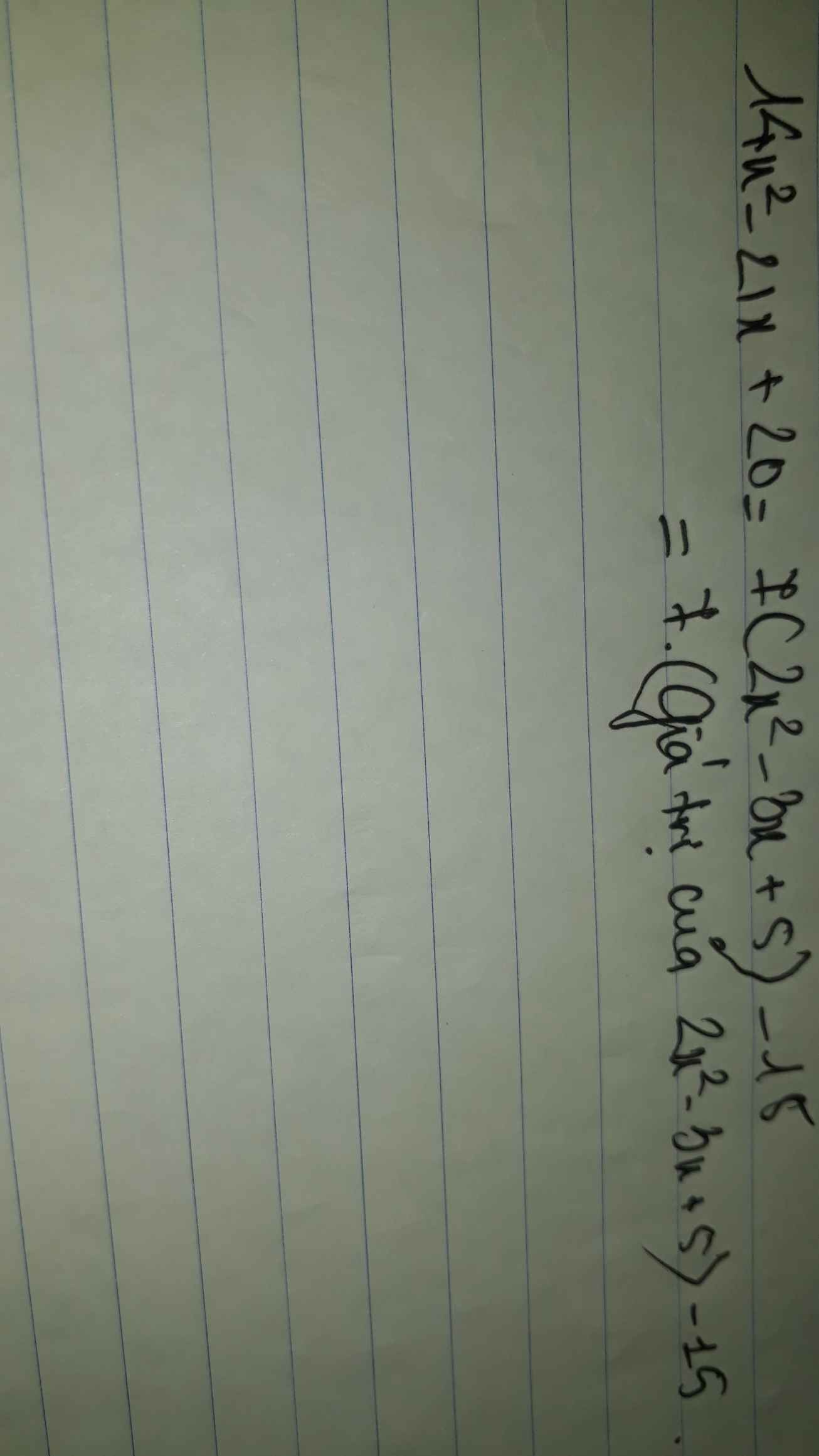
Đúng 3
Bình luận (0)
Với những giá trị nào của x thì a) x3-x2+3x-30b) x3+x2+9x+90c) 4x3-14x2+6x-210d) x2(2x2+3)+2x2-3
Đọc tiếp
Với những giá trị nào của x thì a) x3-x2+3x-3>0b) x3+x2+9x+9<0c) 4x3-14x2+6x-21<0d) x2(2x2+3)+2x2>-3
a) \(x^3-x^2+3x-3>0\)
\(\Leftrightarrow x^2\left(x-1\right)+3\left(x-1\right)>0\)
\(\Leftrightarrow\left(x^2+3\right)\left(x-1\right)>0\)
Mà: \(x^2+3>0\forall x\)
\(\Leftrightarrow x-1>0\)
\(\Leftrightarrow x>1\)
b) \(x^3+x^2+9x+9< 0\)
\(\Leftrightarrow x^2\left(x+1\right)+9\left(x+1\right)< 0\)
\(\Leftrightarrow\left(x^2+9\right)\left(x+1\right)< 0\)
Mà: \(x^2+9>0\forall x\)
\(\Leftrightarrow x+1< 0\)
\(\Leftrightarrow x< -1\)
d) \(4x^3-14x^2+6x-21< 0\)
\(\Leftrightarrow2x^2\left(2x-7\right)+3\left(2x-7\right)< 0\)
\(\Leftrightarrow\left(2x^2+3\right)\left(2x-7\right)< 0\)
Mà: \(2x^2+3>0\forall x\)
\(\Leftrightarrow2x-7< 0\)
\(\Leftrightarrow2x< 7\)
\(\Leftrightarrow x< \dfrac{7}{2}\)
d) \(x^2\left(2x^2+3\right)+2x^2>-3\)
\(\Leftrightarrow2x^4+3x^2+2x^2+3>0\)
\(\Leftrightarrow2x^4+5x^2+3>0\)
\(\Leftrightarrow\left(x^2+1\right)\left(2x^2+3\right)>0\)
Mà:
\(x^2+1>0\forall x\)
\(2x^2+3>0\forall x\)
\(\Rightarrow x\in R\)
Đúng 2
Bình luận (0)
a: =>x^2(x-1)+3(x-1)>0
=>(x-1)(x^2+3)>0
=>x-1>0
=>x>1
b: =>x^2(x+1)+9(x+1)<0
=>(x+1)(x^2+9)<0
=>x+1<0
=>x<-1
c: 4x^3-14x^2+6x-21<0
=>2x^2(2x-7)+3(2x-7)<0
=>2x-7<0
=>x<7/2
d: =>x^2(2x^2+3)+2x^2+3>0
=>(2x^2+3)(x^2+1)>0(luôn đúng)
Đúng 1
Bình luận (0)
Cộng các phân thức khác mẫu thức:
3
2
x
+
3
x
-
3
2
x
-
1
+
2
x
2
+
1
4
x
2
-
2
x
Đọc tiếp
Cộng các phân thức khác mẫu thức: 3 2 x + 3 x - 3 2 x - 1 + 2 x 2 + 1 4 x 2 - 2 x
Mẫu thức chung: 4 x 2 - 2 x = 2 x 2 x - 1
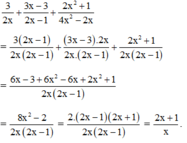
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức:
(
8
x
3
–
4
x
2
)
:
(
2
x
2
)
–
(
4
x
2
–
3
x
)
:
x
+...
Đọc tiếp
Tính giá trị của biểu thức:
( 8 x 3 – 4 x 2 ) : ( 2 x 2 ) – ( 4 x 2 – 3 x ) : x + 2 x , với x = -1
(8x3 – 4x2) : (2x2) – (4x2 – 3x ) : x + 2x
= 4x – 2 – (4x – 3) + 2x = 4x – 2 – 4x + 3 + 2x = 2x + 1
Thay x = -1, ta được: 2.(-1) + 1 = -1
Đúng 0
Bình luận (0)
Cho phương trình x(3x-4)=2x2 +5 có 2 nghiệm x1; x2Không giải phương trình hãy tính giá trị của biểu thức sau:A=2(x1 - x2 )2 +3x1x2
Ta có: \(x\left(3x-4\right)=2x^2+5\)
\(\Leftrightarrow3x^2-4x-2x^2-5=0\)
\(\Leftrightarrow x^2-4x-5=0\)(1)
a=1; b=-4; c=-5
Vì ac=-5<0 nên phương trình (1) có hai nghiệm phân biệt trái dấu
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1\cdot x_2=-5\end{matrix}\right.\)
Ta có: \(A=2\left(x_1-x_2\right)^2+3x_1x_2\)
\(=2\cdot\left(x_1+x_2\right)^2-4\cdot x_1\cdot x_2+3x_1\cdot x_2\)
\(=2\cdot4^2-4\cdot\left(-5\right)+3\cdot\left(-5\right)\)
\(=32+20-15=37\)
Đúng 1
Bình luận (0)
\(x(3x-4)=2x^2+5\\\leftrightarrow 3x^2-4x-2x_2-5=0\\\leftrightarrow x^2-4x-5=0\)
Theo Viét
\(\begin{cases}x_1+x_2=4\\x_1x_2=-5\end{cases}\)
\(A=2(x_1-x_2)^2+3x_1x_2\\=2(x_1^2-2x_1x_2+x_2^2)+3x_1x_2\\=2[(x_1+x_2)^2-4x_1x_2]+3x_1x_2\\=2.[4^2-4.(-5)]+3.(-5)\\=2.36-15\\=57\)
Vậy \(A=62\)
Đúng 0
Bình luận (0)
Thực hiện phép chia đa thức sau bằng cách đặt tính chia:
a) (6x3 – 2x2 – 9x + 3) : (3x – 1)
b) (4x4 + 14x3 – 21x – 9) : (2x2 – 3)
a) Tính tích của đơn thức 5x2y2 và đơn thức 3xy3 rồi tìm bậc của kết quả. b) Tính giá trị của biểu thức A = 2x2 - 3x + 1 tại x = -1
** Bạn lưu ý viết đề bằng công thức toán (nhấn vô biểu tượng $\sum$)
Lời giải:
a)
$5x^2y^2.3xy^3=15x^3y^5$
Bậc của đa thức là: $3+5=8$
b) Tại $x=-1$ thì $A=2(-1)^2-3(-1)+1=6$
Đúng 1
Bình luận (0)
Cho phương trình
2
x
2
+
3
x
−
14
2
2
x
2
+
3
x
−
10
3
. Giả sử
x
1
,
x
2
là 2 nghiệm của phương trình....
Đọc tiếp
Cho phương trình 2 x 2 + 3 x − 14 = 2 2 x 2 + 3 x − 10 3 . Giả sử x 1 , x 2 là 2 nghiệm của phương trình. Tính giá trị biểu thức A = x 1 2 + x 2 2 − 4 x 1 x 2
A. 2
B. 225 4
C. 3 4
D. 15 2

Khi đó phương trình trở thành:
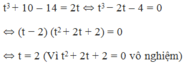
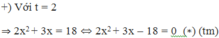
Giả sử x 1 , x 2 là hai nghiệm của phương trình (*)
Theo Vi – et, ta có x 1 + x 2 = − 3 2 x 1 . x 2 = − 9
⇒ A = x 1 2 + x 2 2 − 4 x 1 x 2 = x 1 + x 2 2 − 6 x 1 . x 2 = 9 4 + 54 = 225 4 = 15 2
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức sau:
a) A = 2x2 - y2 tại x = -1; y = 2
b) B = 3x + 5xy2 tại x = 1; y = -2
Tính giá trị của biểu thức sau:
a) A = 2x2 - y2 tại x = -1; y = 2
Thay x = - 1 và y = 2 ta có:
A = 2 . ( - 1 ) 2 - 22 = -2
Vậy tại x = -1; y = 2 thì giá trị của biểu thức là - 2
b) B = 3x + 5xy2 tại x = 1; y = -2
Thay x = 1 và y = - 2 ta có:
B = 3 .1 + 5 . 1 . ( - 2 )2 = 23
Vậy tại x = 1; y = - 2 thì giá trị của biểu thức là 23
Đúng 2
Bình luận (0)























