TXĐ: \(D=R\)

\(y'=\dfrac{-x^2+2x+2}{\left(x^2-2x+4\right)^2}=0\Rightarrow x=1\pm\sqrt{3}\)

Dấu của y' trên trục số:

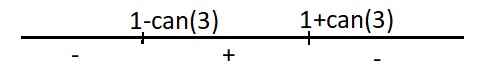
Hàm đồng biến trên \(\left(1-\sqrt{3};1+\sqrt{3}\right)\)

Hàm nghịch biến trên các khoảng \(\left(-\infty;1-\sqrt{3}\right)\) và \(\left(1+\sqrt{3};+\infty\right)\)

TXĐ: D = R \ {-2}

Ta có: \(y'=\dfrac{\left(-2x+2\right)\left(x+2\right)-\left(-x^2+2x-1\right)}{\left(x+2\right)^2}=\dfrac{-x^2-4x+5}{\left(x+2\right)^2}\)

\(y'=0\Rightarrow-x^2-4x+5=0\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)

⇒ Hàm số y đồng biến trên (-5, -2) và (-2, 1)

Hàm số y nghịch biến trên (-∞, -5) và (1, +∞)

Chắc là đề ko đúng đâu, vì cực trị (tức là điểm mà tại đó mà hàm đổi tính chất từ đồng biến sang nghịch biến) của bài này rất xấu, nó là giá trị x thỏa mãn \(sinx=\dfrac{3}{5}\). Với lượng giác thì đây là 1 giá trị cực xấu.

cả nhà giúp mình với mai minh kiểm tra chất lượng rồi. Thanks all.

a: Hàm số đồng biến trên R

b: Hàm số nghịch biến trên R

Bạn kiểm tra lại đề. Và vào hoc 24 để đăng nhé! 

Làm câu cuối:

TXĐ: \(x\in\)[ 0 ; + vô cùng ) 

\(y'=\frac{1}{2\sqrt{x}}-1=0\Leftrightarrow2\sqrt{x}=1\Leftrightarrow x=\frac{1}{4}\left(tm\right)\)

Vẽ bảng biến thiên: 

....

Từ bảng biên thiên: 

Hàm số đồng biến trong khoảng ( 0 ; 1/4 ) 

Hàm số nghịch biên trong khoảng ( 1/4 ; + dương vô cùng)

Tập xác định \(x< \frac{1}{2}\)

Ta có : \(y'=1-\frac{2}{1-2x}=\frac{-1-2x}{1-2x}\Rightarrow y'=0\Leftrightarrow x=-\frac{1}{2}\)

Hàm số đồng biến trên \(\left(-\infty;-\frac{1}{2}\right)\) 

Hàm số nghịch biến trên \(\left(-\frac{1}{2};\frac{1}{2}\right)\)