a. 

$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$

b.

$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$

c.

$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$

d.

$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$

$=(x+1)(x^2-4x+1)$

e.

$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$

$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$

f.

$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$

$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$

g.

$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$

$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$

$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$

$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$

h.

$x^6+2x^5+x^4-2x^3-2x^2+1$

$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$

$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$

\(=x^3+64\\ =x^3-27y^3\\ =x^6-\dfrac{1}{27}\)

\(\left(x+4\right)\left(x^2-4x+16\right)=x^3+64\)

\(\left(x-3y\right)\left(x^2+3xy+9y^2\right)=x^3-27y^3\)

\(\left(x^2-\dfrac{1}{3}\right)\left(x^4+\dfrac{1}{3}x^2+\dfrac{1}{9}\right)=x^6-\dfrac{1}{27}\)

a) \(\left(2x+3y\right)^2=\left(2x\right)^2+2\cdot2x\cdot3y+\left(3y\right)^2=4x^2+12xy+9y^2\)

b) \(\left(x+\dfrac{1}{4}\right)^2=x^2+2\cdot x\cdot\dfrac{1}{4}+\left(\dfrac{1}{4}\right)^2=x^2+\dfrac{1}{2}x+\dfrac{1}{16}\)

c) \(\left(x^2+\dfrac{2}{5}y\right)\left(x^2-\dfrac{2}{5}y\right)=\left(x^2\right)^2-\left(\dfrac{2}{5}y\right)^2=x^4-\dfrac{4}{25}y^2\)

d) \(\left(2x+y^2\right)^3=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y^2+3\cdot2x\cdot\left(y^2\right)^2+\left(y^2\right)^3=8x^3+12x^2y^2+6xy^4+y^6\)

e) \(\left(3x^2-2y\right)^2=\left(3x^2\right)^2-2\cdot3x^2\cdot2y+\left(2y\right)^2=9x^4-12x^2y+4y^2\)

f) \(\left(x+4\right)\left(x^2-4x+16\right)=x^3+4^3=x^3+64\)

g) \(\left(x^2-\dfrac{1}{3}\right)\cdot\left(x^4+\dfrac{1}{3}x^2+\dfrac{1}{9}\right)=\left(x^2\right)^3-\left(\dfrac{1}{3}\right)^3=x^6-\dfrac{1}{27}\)

ghi ko hiểu j hết mẹ!!???????

1)(x²-4x+16)(x+4)-x(x+1)(x+2)+3x²=0

\(\Rightarrow\)(x³+64)-x(x²+2x+x+2)+3x²=0

\(\Rightarrow\)x³+64-x³-2x²-x²-2x+3x²=0

\(\Rightarrow\)-2x+64=0

\(\Rightarrow\)-2x=-64

\(\Rightarrow\)x=\(\dfrac{-64}{-2}\)

\(\Rightarrow x=32\)

2)(8x+2)(1-3x)+(6x-1)(4x-10)=-50

\(\Rightarrow\)8x-24x²+2-6x+24x²-60x-4x+10=50

\(\Rightarrow\)-62x+12=50

\(\Rightarrow\)-62x=50-12

\(\Rightarrow\)-62x=38

\(\Rightarrow\)x=\(-\dfrac{38}{62}=-\dfrac{19}{31}\)

3)(x²+2x+4)(2-x)+x(x-3)(x+4)-x²+24=0

\(\Rightarrow\)8-x³+x(x²+4x-3x-12)-x²+24=0

\(\Rightarrow\)8-x³+x³+4x²-3x²-12x-x²+21=0

\(\Rightarrow\)-12x+29=0

\(\Rightarrow\)-12x=-29

\(\Rightarrow\)x=\(\dfrac{-29}{-12}=\dfrac{29}{12}\)

a) TXĐ: R

y′ = 6x − 24 x 2  = 6x(1 − 4x)

y' = 0 ⇔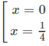 

y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)

y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )

b) TXĐ: R

y′ = 16 + 4x − 16 x 2  − 4 x 3  = −4(x + 4)( x 2  − 1)

y' = 0 ⇔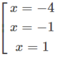 

Bảng biến thiên:

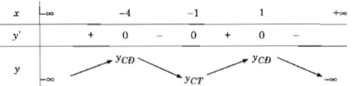
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )

c) TXĐ: R

y′ = 3 x 2 − 12x + 9

y' = 0

y' > 0 trên các khoảng ( - ∞ ; 1), (3;  + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3;  + ∞ )

y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)

d) TXĐ: R

y′ = 4 x 3  + 16 = 4x( x 2  + 4)

y' = 0 ⇔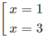 

y' > 0 trên khoảng (0;  + ∞ ) ⇒ y đồng biến trên khoảng (0;  + ∞ )

y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)

a) \(x^4+8x+63\)

\(=x^4+4x^3+9x^2-4x^3-16x^2-36x+7x^2+28x+63\)

\(=x^2\left(x^2+4x+9\right)-4x\left(x^2+4x+9\right)+7\left(x^2+4x+9\right)\)

\(=\left(x^2+4x+9\right)\left(x^2-4x+7\right)\)

c) \(\left(x^2+2x+7\right)+\left(x^2-2x+4\right)\left(x^2+2x+3\right)\left(1\right)\)

Ta có : \(x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)

\(\Rightarrow x^2+2x+4=\dfrac{x^3-8}{x-2}\)

\(\left(1\right)\Rightarrow\left[\left(\dfrac{x^3-8}{x-2}+3\right)\right]+\left(x^2-2x+4\right)\left[\left(\dfrac{x^3-8}{x-2}-1\right)\right]\)

\(=\left[\left(\dfrac{x^3-3x-14}{x-2}\right)\right]+\left(x^2-2x+4\right)\left[\left(\dfrac{x^3-2x-5}{x-2}\right)\right]\)

\(=\dfrac{1}{x-2}\left[x^3-3x-14+\left(x^2-2x+4\right)\left(x^3-2x-5\right)\right]\)

a) Ta có: \(36x^3-4x=0\)

\(\Leftrightarrow4x\left(9x^2-1\right)=0\)

\(\Leftrightarrow x\left(3x-1\right)\left(3x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=\dfrac{-1}{3}\end{matrix}\right.\)

b) Ta có: \(3x\left(x-2\right)+x-2=0\)

\(\Leftrightarrow\left(x-2\right)\left(3x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-1}{3}\end{matrix}\right.\)

d) Ta có: \(x^2-6x-16=0\)

\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)

e) Ta có: \(x^4-6x^2-7=0\)

\(\Leftrightarrow\left(x^2-7\right)\left(x^2+1\right)=0\)

\(\Leftrightarrow x\in\left\{\sqrt{7};-\sqrt{7}\right\}\)