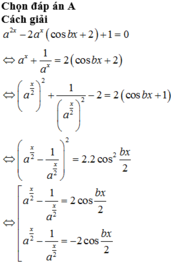a: Khi m=1 thì phương trình sẽ là:

\(x^2-2x+1-1=0\)

=>x^2-2x=0

=>x(x-2)=0

=>x=0 hoặc x=2

b: \(\text{Δ}=\left(-2\right)^2-4\left(m-1\right)=4-4m+4=-4m+8\)

Để phương trình có 2 nghiệm thì -4m+8>=0

=>-4m>=-8

=>m<=2

\(x_1^3+x_2^3< =15\)

=>\(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)< =15\)

=>\(2^3-3\cdot2\cdot\left(m-1\right)< =15\)

=>\(8-6m+6< =15\)

=>-6m+14<=15

=>-6m<=1

=>\(m>=-\dfrac{1}{6}\)

=>\(-\dfrac{1}{6}< =m< =2\)

a: Thay x=-1 vào (6), ta được:

1+2m+m+6=0

=>3m+7=0

=>m=-7/3

x1+x2=-2m/1=-2*7/3=-14/3

=>x2=-14/3-x1=-14/3+1=-11/3

b: \(\text{Δ}=0^2-2\left(2m+m+6\right)=-2\left(3m+6\right)\)

Để phương trình có nghiệm kép thì 3m+6=0

=>m=-2

Khi m=-2 thì (6) sẽ là x^2+2*(-2)-2+6=0

=>x^2-4x+4=0

=>x=2

Chọn B

1.Ta có \(\Delta=4m^2-4\left(m^2-m-3\right)=4m+12\)

Để phương trình có 2 nghiệm phân biệt \(\Rightarrow\Delta>0\Rightarrow4m+12>0\Rightarrow m>-3\)

Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=2m\\x_1.x_2=m^2-m-3\end{cases}}\)

a. Phương trình có 2 nghiệm trái dấu \(\Rightarrow x_1.x_2< 0\Rightarrow m^2-m-3< 0\Rightarrow\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)

Vậy \(\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)

b. Phương trình có 2 nghiệm phân biệt dương \(\Leftrightarrow\hept{\begin{cases}x_1+x_2=2m>0\\x_1.x_2=m^2-m-3>0\end{cases}\Leftrightarrow\hept{\begin{cases}m>0\\m< \frac{1-\sqrt{13}}{2}\end{cases}\left(l\right);\hept{\begin{cases}m>0\\m>\frac{1+\sqrt{13}}{2}\end{cases}\Leftrightarrow m>\frac{1+\sqrt{13}}{2}}}}\)

Vậy \(m>\frac{1+\sqrt{13}}{2}\)

2. a.Ta có \(\Delta=\left(2m-1\right)^2+4m=4m^2-4m+1+4m=4m^2+1\)

Ta thấy \(\Delta=4m^2+1>0\forall m\)

Vậy phương trình luôn có 2 nghiejm phân biệt với mọi m

b. Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=1-2m\\x_1.x_2=-m\end{cases}}\)

Để \(x_1-x_2=1\Leftrightarrow\left(x_1-x_2\right)^2=1\Leftrightarrow\left(x_1+x2\right)^2-4x_1x_2=1\)

\(\Leftrightarrow\left(1-2m\right)^2-4.\left(-m\right)=1\Leftrightarrow4m^2-4m+1+4m=1\)

\(\Leftrightarrow m^2=0\Leftrightarrow m=0\)

Vậy \(m=0\)thoă mãn yêu cầu bài toán 

TL :

Đề sai

\(x1^2\)là số gì

HT

Ý bạn ấy là \(x_1^2\)nhưng bạn ấy chưa biết chỗ để đánh chỉ số dưới. Bạn nhấn vào cái biểu tượng x₂ ở chỗ khung điều chỉnh thì con trỏ hạ xuống để bạn gõ chỉ số dưới. Xong rồi thì nhấn vào biểu tượng đó lần nữa.

Xét pt \(x^2-2\left(m-4\right)x+2m-20=0\), có \(a=1;b=-2\left(m-4\right);c=2m-20\)

Ta có \(\Delta=b^2-4ac=\left[-2\left(m-4\right)\right]^2-4.1.\left(2m-20\right)\)
\(=4\left(m-4\right)^2-8m+80\)\(=4\left(m^2-8m+16\right)-8m+80\)\(=4m^2-32m+64-8m+80\)\(=4m^2-40m+144\)\(=4\left(m^2-10m+25\right)+44\)\(=4\left(m-5\right)^2+44\)

Do \(\left(m-5\right)^2\ge0\Leftrightarrow4\left(m-5\right)^2+44\ge44>0\Leftrightarrow\Delta>0\)

Vậy pt đã cho luôn có 2 nghiệm phân biệt.

\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)

\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)

\(b,\left(m-1\right)x^2-2mx+m-2=0\)

\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)

\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)

\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)

\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)

\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

\(a,x=-1\\ \Leftrightarrow1-2\left(m+1\right)+m^2-3m=0\\ \Leftrightarrow-1-5m+m^2=0\\ \Leftrightarrow m^2-5m-1=0\\ \Delta=25+4=29\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{5+\sqrt{29}}{2}\\m=\dfrac{5-\sqrt{29}}{2}\end{matrix}\right.\)

\(b,\)Pt có 2 nghiệm phân biệt

\(\Leftrightarrow\Delta=\left[2\left(m+1\right)\right]^2-4\left(m^2-3m\right)>0\\ \Leftrightarrow4m^2+8m+4-4m^2+12m>0\\ \Leftrightarrow20m+4>0\Leftrightarrow m>-\dfrac{1}{5}\)

\(c,\)Để pt có nghiệm duy nhất (nghiệm kép)

\(\Leftrightarrow\Delta=\left[2\left(m+1\right)\right]^2-4\left(m^2-3m\right)=0\\ \Leftrightarrow20m+4=0\\ \Leftrightarrow m=-\dfrac{1}{5}\)

a) Thay \(a=0\) vào phương trình, ta được:

 \(x^2-2x-3=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)

Vậy ...

b) Ta có: \(\Delta'=4-3a\) 

Để phương trình có 2 nghiệm x₁ và x₂ \(\Leftrightarrow\Delta'\ge0\) \(\Leftrightarrow a\le\dfrac{4}{3}\)

 Vậy ...

c) Phương trình có nghiệm bằng -1 

\(\Rightarrow1+2\left(1-a\right)+a^2+a-3=0\) 

\(\Leftrightarrow a^2-a=0\) \(\Rightarrow\left[{}\begin{matrix}a=1\\a=0\end{matrix}\right.\)

Vậy ... 

pt: \(x^2+2\left(a-1\right)x+a^2+a-3=0\) (1)

a) khi a=0 pt(1) \(\Leftrightarrow x^2-2x-3=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)

b) \(\Delta'=b'^2-ac=\left(a-1\right)^2-\left(a^2+a-3\right)=-3a+4\)

phương trình có 2 nghiệm phân biệt khi \(\Delta'>0\Leftrightarrow-3a+4>0\Leftrightarrow a< \dfrac{4}{3}\)

c) pt(1) có nghiệm x=-1 \(\Leftrightarrow\left(-1\right)^2+2\left(a-1\right).\left(-1\right)+a^2+a-3=0\)

\(\Leftrightarrow a^2-a=0\Leftrightarrow\left[{}\begin{matrix}a=0\\a=1\end{matrix}\right.\)