Cho phân số \(A=\dfrac{n+1}{n-3},\left(n\in\mathbb{Z};n\ne3\right)\)
Tìm n để A là phân số tối giản ?
Những câu hỏi liên quan
Có thể có phân số \(\dfrac{a}{b},\left(a,b\in\mathbb{Z},b\ne0\right)\) sao cho :
\(\dfrac{a}{b}=\dfrac{a.m}{b.n},\left(m,n\in\mathbb{Z};m,n\ne0,m\ne n\right)\) hay không ?
Có thể có phân số a/b (a, b ∈ Z, b ≠ 0) sao cho:
(m, n ∈ Z, m , n ≠ 0 , m ≠ n) khi và chỉ khi a = 0
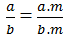
Vì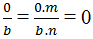 
(m, n ∈ Z, m , n ≠ 0 , m ≠ n)
Đúng 0
Bình luận (0)
Điền kí hiệu \(\left(\in,\notin,\subset,\cap\right)\) thích hợp vào chỗ trống :
a) \(\dfrac{-3}{4}.....\mathbb{Z}\)
b) \(0.....\mathbb{N}\)
c) \(3,275.......\mathbb{N}\)
d) \(\mathbb{N}.......\mathbb{Z}=\mathbb{N}\)
e) \(\mathbb{N}.......\mathbb{Z}\)
a) \(-\dfrac{3}{4}\notin Z\)
b) \(0\in N\)
c) \(3,275\notin N\)
d) \(N\cap Z=N\)
e) \(N\subset Z\)
Đúng 0
Bình luận (0)
Viết các biểu thức số sau dưới dạng \(a^n,\left(a\in\mathbb{Q},n\in\mathbb{N}\right)\) :
a) \(9.3^3.\dfrac{1}{81}.3^2\)
b) \(4.2^5:\left(2^3.\dfrac{1}{16}\right)\)
c) \(3^2.2^5.\left(\dfrac{2}{3}\right)^2\)
d) \(\left(\dfrac{1}{3}\right)^2.\dfrac{1}{3}.9^2\)
a) \(3^3\)
b)\(2^8\)
c) \(2^7\)
d) \(3^1\)
Đúng 0
Bình luận (0)
a) 9.33.\(\dfrac{1}{81}\) .32 = 32. 33.\(\dfrac{1}{3^4}\) . 32 = 33
b) 4. 25: \(\) (23.\(\dfrac{1}{16}\))= 22. 25: 23. \(\dfrac{1}{2^4}\) = 27: \(\dfrac{1}{2}\) = 27. 2= 28
c) 32. 25. \(\left(\dfrac{2}{3}\right)^2\) = 32. 25. \(\dfrac{2^2}{3^2}\) = 25. 22 = 27
d) \(\left(\dfrac{1}{3}\right)^2\) .\(\dfrac{1}{3}\) . 92 = \(\dfrac{1}{9}.\dfrac{1}{3}\). 92 = \(\dfrac{9}{3}\) = 31
Đúng 0
Bình luận (2)
a không bít !
b chịu
c quên rồi
d . . .
Đúng 0
Bình luận (7)
Xem thêm câu trả lời
Các phát biểu sau đúng hay sai?
a) \(9 \in \mathbb{N}\) b) \( - 6 \in \mathbb{N}\)
c) \( - 3 \in \mathbb{Z}\) d) \(0 \in \mathbb{Z}\)
e) \(5 \in \mathbb{Z}\) g) \(20 \in \mathbb{N}\)
a) Đúng vì 9 là số tự nhiên
b) Sai vì \( - 6\) là số nguyên âm, không phải là số tự nhiên.
c) Đúng vì \( - 3\) là số nguyên âm nên nó là số nguyên.
d) Đúng vì 0 là số nguyên
e) Đúng vì số 5 là số nguyên dương nên nó là số nguyên.
g) Đúng vì 20 là số tự nhiên.
Đúng 0
Bình luận (0)
a) Cho hai phân số dfrac{1}{n} và dfrac{1}{n+1},left(ninmathbb{Z},n0right). Chứng tỏ rằng tích của hai phân số này bằng hiệu của chúng ?
b) Áp dụng kết quả trên để tính giá trị của các biểu thức sau :
Adfrac{1}{2}.dfrac{1}{3}+dfrac{1}{3}.dfrac{1}{4}+dfrac{1}{4}.dfrac{1}{5}+dfrac{1}{5}.dfrac{1}{6}+dfrac{1}{6}.dfrac{1}{7}+dfrac{1}{7}.dfrac{1}{8}+dfrac{1}{8}.dfrac{1}{9}
Bdfrac{1}{30}+dfrac{1}{42}+dfrac{1}{56}+dfrac{1}{72}+dfrac{1}{90}+dfrac{1}{110}+dfrac{1}{132}
Đọc tiếp
a) Cho hai phân số \(\dfrac{1}{n}\) và \(\dfrac{1}{n+1},\left(n\in\mathbb{Z},n>0\right)\). Chứng tỏ rằng tích của hai phân số này bằng hiệu của chúng ?
b) Áp dụng kết quả trên để tính giá trị của các biểu thức sau :
\(A=\dfrac{1}{2}.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{4}+\dfrac{1}{4}.\dfrac{1}{5}+\dfrac{1}{5}.\dfrac{1}{6}+\dfrac{1}{6}.\dfrac{1}{7}+\dfrac{1}{7}.\dfrac{1}{8}+\dfrac{1}{8}.\dfrac{1}{9}\)
\(B=\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}+\dfrac{1}{132}\)
a. Ta có:
b. Theo kết quả câu a,ta có:
Đúng 0
Bình luận (0)
Đọc những điều ghi sau đây và cho biết điều đó có đúng không ?
\(-2\in\mathbb{N},6\in\mathbb{N},0\in\mathbb{N},0\in\mathbb{Z},-1\in\mathbb{N},-1\in\mathbb{Z}\)
\(-2\in N\rightarrow Sai:\) . -2 không thuộc Z
\(6\in N\rightarrow\) Đúng
\(0\in N\rightarrow\) Đúng
\(0\in Z\rightarrow\) Đúng
\(-1\in N\rightarrow Sai\) . -1 không thuộc N
\(-1\in Z\rightarrow\) Đúng
Đúng 0
Bình luận (0)
\(-2\in N\rightarrow Sai\) \(\left(-2\notin N\right)\)
\(6\in N\rightarrowĐúng\)
\(0\in N\rightarrowĐúng\)
\(0\in Z\rightarrowĐúng\)
\(-1\in N\rightarrow Sai\) \(\left(-1\notin N\right)\)
\(-1\in Z\rightarrowĐúng\)
Đúng 0
Bình luận (0)
−2∈N→Sai:−2∈N→Sai: . -2 không thuộc Z
6∈N→6∈N→ Đúng
0∈N→0∈N→ Đúng
0∈Z→0∈Z→ Đúng
−1∈N→Sai−1∈N→Sai . -1 không thuộc N
−1∈Z→−1∈Z→ Đúng
Đúng 0
Bình luận (0)
Chứng tỏ rằng \(\dfrac{12n+1}{30n+2}\) là phân số tối giản \(\left(n\in\mathbb{N}\right)\)
Gọi ƯCLN (12n+1,30n+2) là d
\(\Rightarrow\left(12n+1\right)⋮d\)
\(\left(30n+2\right)⋮d\)
\(\Rightarrow5\left(12n+1\right)-2\left(30n+2\right)⋮d\)
\(\Rightarrow60n+5-60n-4⋮d\)
\(\Rightarrow1⋮d\Leftrightarrow d=1\)
Vậy ƯCLN \(\left(12n+1,30n+2\right)=1\Leftrightarrow\dfrac{12n+1}{30n+2}\) là p/s tối giản \(\left(dpcm\right)\)
Đúng 0
Bình luận (0)
Gọi ước chung lớn nhất của 12n+1 và 30n+ 2 là d
\(\Rightarrow\) ( 12n+1) \(⋮\) d và ( 30n+2 ) \(⋮\) d
\(\Rightarrow\) \(\left[5\left(12n+1\right)-2\left(30n+2\right)\right]⋮d\)
\(\Leftrightarrow\) ( 60n + 5 - 60n - 4 ) \(⋮d\)
\(\Leftrightarrow\) 1 \(⋮\) d hay d= 1
Vậy ước chung lớn nhất của 12n+ 1 và 30n+2 là 1 hay \(\dfrac{12n+1}{30n+2}\) là phân số tối giản .
Đúng 0
Bình luận (0)
Gọi d là UWCLN của ( 12n + 1 , 30n + 2 )
=> \(12n+1⋮d\Rightarrow5\left(12n+1\right)⋮d\Rightarrow60n+5⋮d\)
\(\Rightarrow30n+2⋮d\Rightarrow2\left(30n+2\right)⋮d\Rightarrow60n+4⋮d\)
\(\Rightarrow\left(60n+5\right)-\left(60n+4\right)⋮d\Rightarrow60n+5-60n-4⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
\(\Rightarrow\dfrac{12n+1}{30n-2}\) là phân số tối giản ( ĐPCM )
Đúng 0
Bình luận (0)
Cho 2 tập hợp, A {xin mathbb Z | left(2x^2-x-3right)left(x^2-4right)0} , B {xin mathbb N | xle4}. Viết tập hợp bằng cạc liệt kê các phần tử.
Đọc tiếp
Cho 2 tập hợp, A = {\(x\in \mathbb Z\) | \(\left(2x^2-x-3\right)\left(x^2-4\right)=0\)} , B = {\(x\in \mathbb N\) | 
\(x\le4\)}.
Viết tập hợp bằng cạc liệt kê các phần tử.
(Bấm máy tính tìm nghiệm)
\(A=\left\{-2;-1;2\right\}\)
\(B=\left\{0;1;2;3\right\}\)
Đúng 1
Bình luận (0)
Các phát biểu sau đúng hay sai? Nếu sai hãy phát biểu lại cho đúng.
a) \( - 4 \in \mathbb{Z}\) b) \(5 \in \mathbb{Z}\) c) \(0 \in \mathbb{Z}\)
d) \( - 8 \in \mathbb{N}\) e) \(6 \in \mathbb{N}\) g) \(0 \in \mathbb{N}\)
Phát biểu a : Đúng, vì \( - 4\) là số nguyên âm nên nó là số nguyên.
Phát biểu b: Đúng, vì 5 là số nguyên dương nên nó là số nguyên.
Phát biểu c: Đúng, vì 0 là số nguyên.
Phát biểu d: Sai, vì \( - 8\) là số nguyên âm, không phải là số tự nhiên.
Phát biểu e: Đúng, vì 6 là số tự nhiên.
Phát biểu f: Đúng, vì 0 là số tự nhiên.
Đúng 0
Bình luận (0)